
Лабораторна робота № 4. Основні способи зведення мережевої задачі до матричної форми
4.1. Завдання до лабораторної роботи
1. Розв'язати мережеву ТЗ без обмежень на пропускні здатності за допомогою Excel-таблиці, одержати оптимальний план перевезень за допомогою “EXCEL -2003”. Проаналізувати результати.
2. Розв'язати мережеву ТЗ з обмеженнями на пропускні здатності за допомогою Excel-таблиці, одержати оптимальний план перевезень за допомогою “EXCEL -2003”. Проаналізувати результати.
4.2. Варіанти завдань
Додати до транспортної мережі без обмежень на пропускні здатності (рис. 4.1) та транспортної мережі з обмеженнями на пропускні здатності замовлень (рис. 4.2) один пункт постачання з обсягом 5 одиниць вантажу, один пункт споживання з обсягом 5 одиниць вантажу та один проміжний транспортний пункт.
2.3. Методичні вказівки до виконання лабораторної роботи
На рис. 4.1 зображена мережа з 7 вершинами і 11 ланками. Поруч із відповідною вершиною у дужках числом зі знаком плюс показаний обсяг виробництва, а обсяг споживання, відповідно, числом зі знаком мінус. Вартість перевезення вантажу вписана в кожну дугу. Також на рис. 4.1 подані розподіли вантажопотоків і потенціалів.

Рис. 4.1. Приклад ТМ без Рис. 4.2. Приклад ТМ з
обмежень на пропускні здатності обмеженнями на пропускні здатності
Перший спосіб – Ордена А. показаний у табл. 4.1. Кожній вершині мережі виділяється рядок і стовпець. Таким чином у нашому випадку, таблиця складається із семи рядків і семи стовпців. Вона завжди повинна бути квадратною. У клітинках головної діагоналі таблиці 4.1, 2.2 і т. д. вартість перевезення дорівнює 0, тому що вихідних і одночасно вхідних дуг до тієї самої вершини бути не може.
Для вершин, з'єднаних між собою ланкою, у клітинках таблиці на перетинанні відповідних рядків і стовпців проставлена вартість транспортування цією ланкою. Інші клітинки заблоковані більшими, порівняно з вартостями перевезень, числами (у табл. 2.1 це незаповнені клітинки).
Для зручності розрахунку до значення обсягу виробництва (споживання) до кожної вершини додається яке-небудь позитивне число. У табл. 4.1 це число 9. Таким чином, обсяг виробництва у вершині 1 буде 7+9=16, у транзитній вершині 2 – 9, так само як і обсяг споживання і т. д. Потім ТЗ розв'язують будь-яким відомим методом. У табл. 4.1 показаний остаточний результат рішення задачі – значення оптимального плану перевезень вантажу виділені курсивом, а на рис. 4.3 – результат розв'язання за допомогою Excel-таблиці.
Таблиця 4.1
Зведення мережевої транспортної задачі до матричної форми
методом Ордена
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|||||||
1 |
0 |
|
4 |
|
6 |
|
3 |
|
|
|
|
16 |
|||
|
9 |
|
2 |
|
1 |
|
4 |
||||||||
2 |
4 |
0 |
|
|
2 |
3 |
|
|
|
9 |
|||||
|
7 |
|
2 |
||||||||||||
3 |
6 |
|
0 |
|
4 |
|
12 |
10 |
9 |
||||||
|
9 |
||||||||||||||
4 |
3 |
2 |
4 |
0 |
|
|
3 |
|
|
11 |
|||||
|
5 |
|
6 |
||||||||||||
5 |
|
3 |
|
|
0 |
|
5 |
|
9 |
||||||
|
9 |
||||||||||||||
6 |
|
|
12 |
3 |
5 |
0 |
|
5 |
|
9 |
|||||
|
3 |
|
6 |
||||||||||||
7 |
|
|
10 |
|
|
5 |
0 |
|
9 |
||||||
|
9 |
||||||||||||||
|
9 |
9 |
10 |
9 |
11 |
9 |
15 |
72 |
|||||||
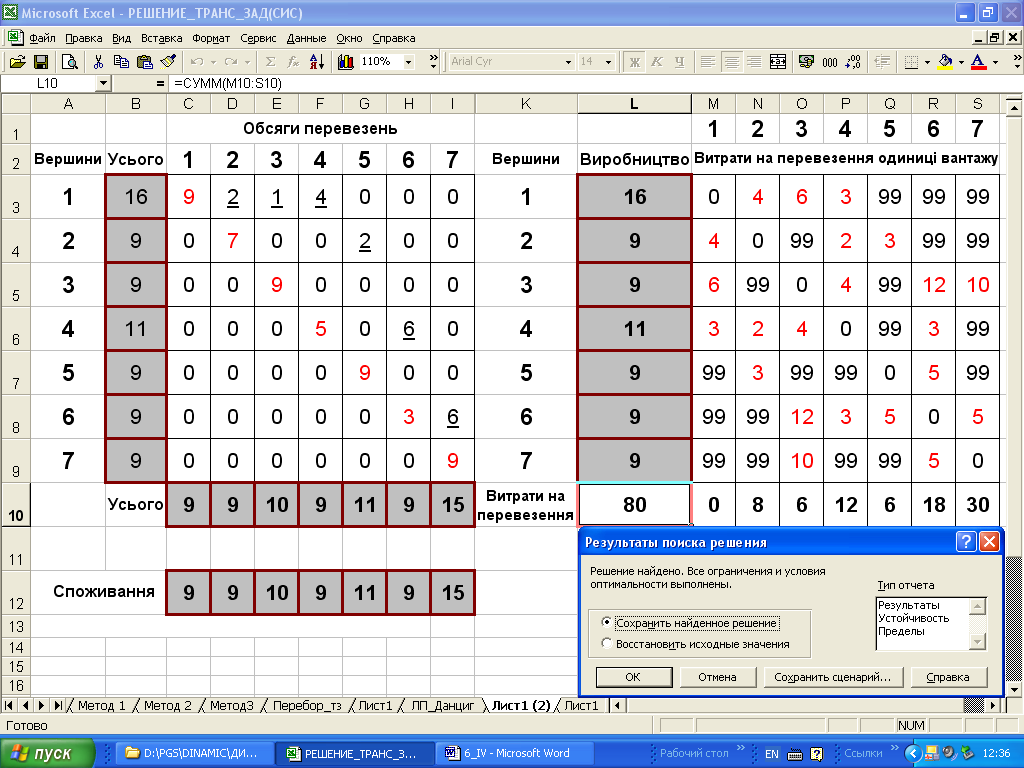
Рис. 4.3. Розв'язання мережевої ТЗ без обмежень на пропускні здатності за допомогою Excel-таблиці
Другий спосіб – спосіб Вагнера Ш.М. Він зручніший для мереж з обмеженнями пропускної здатності. Така мережа зображена на рис. 4.2, де представлений також і оптимальний план перевезень. У табл. 4.2 показано приведення цієї мережі до матричної форми.
Таблиця 4.2
Зведення мережевої задачі до матричної форми методом Вагнера
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|||||||||||
1-2 |
0 |
4 |
|
|
|
|
|
|
1 |
5-2 |
|
3 |
|
|
0 |
|
|
|
3 |
|||||||||
|
1 |
|
3 |
|||||||||||||||||||||||||
2-1 |
4 |
0 |
|
|
|
|
|
|
1 |
4-6 |
|
|
|
0 |
|
|
3 |
|
|
7 |
||||||||
|
1 |
|
1 |
|
6 |
|||||||||||||||||||||||
1-3 |
0 |
|
|
6 |
|
|
|
|
|
2 |
6-4 |
|
|
|
3 |
|
0 |
|
|
7 |
||||||||
|
1 |
|
1 |
|
7 |
|||||||||||||||||||||||
3-1 |
6 |
|
0 |
|
|
|
|
|
2 |
3-6 |
|
|
0 |
|
|
|
12 |
|
2 |
|||||||||
|
2 |
|
2 |
|||||||||||||||||||||||||
1-4 |
0 |
|
|
3 |
|
|
|
|
5 |
6-3 |
|
|
12 |
|
|
0 |
|
|
2 |
|||||||||
|
5 |
|
2 |
|||||||||||||||||||||||||
4-1 |
3 |
|
|
0 |
|
|
|
|
5 |
3-7 |
|
|
0 |
|
|
|
|
10 |
100 |
|||||||||
|
5 |
|
100 |
|||||||||||||||||||||||||
2-4 |
|
0 |
|
|
2 |
|
|
|
5 |
7-3 |
|
|
10 |
|
|
|
0 |
|
100 |
|||||||||
|
5 |
|
100 |
|||||||||||||||||||||||||
4-2 |
|
2 |
|
|
0 |
|
|
|
|
5 |
5-6 |
|
|
|
|
0 |
|
5 |
|
2 |
||||||||
|
1 |
|
4 |
|
2 |
|||||||||||||||||||||||
3-4 |
|
|
0 |
|
4 |
|
|
|
2 |
6-5 |
|
|
|
|
5 |
0 |
|
|
2 |
|||||||||
|
2 |
|
2 |
|||||||||||||||||||||||||
4-3 |
|
|
4 |
0 |
|
|
|
|
2 |
6-7 |
|
|
|
|
|
0 |
|
5 |
|
7 |
||||||||
|
2 |
|
1 |
|
6 |
|||||||||||||||||||||||
2-5 |
|
0 |
|
|
|
3 |
|
|
|
3 |
7-6 |
|
|
|
|
|
5 |
0 |
|
7 |
||||||||
|
1 |
|
2 |
|
7 |
|||||||||||||||||||||||
|
1 |
9 |
107 |
17 |
7 |
18 |
113 |
272 |
||||||||||||||||||||
Для дуг тут відведені рядки, а для вершин стовпці. У верхньому лівому куті клітинки таблиці зазначена вартість перевезення по дузі. Там, де в клітинках немає цифр, передбачається їхнє блокування більшим числом М. числами (у табл. 4.2 це незаповнені клітинки).
Обсяг
виробництва дорівнює пропускній
здатності дуги, тобто
![]() .
Длядуг, де пропускна здатність необмежена,
зокрема для дуг 3–7 і 7–3, вона відповідатиме
(у нашому прикладі) числу – 100.
.
Длядуг, де пропускна здатність необмежена,
зокрема для дуг 3–7 і 7–3, вона відповідатиме
(у нашому прикладі) числу – 100.
Обсяг споживання для виробляючих вершин мережі визначають за формулою:
![]() , (4.1)
, (4.1)
для вершин, які споживають вантаж за формулою:
![]() , (4.2)
, (4.2)
для транзитних вершин за формулою:
![]() . (4.3)
. (4.3)
Таким чином, для вершини 1 обсяг споживання дорівнює 1+5+2–7=1, для вершини 7–7+100+6=113, а для вершини 2–1+5+3=9. У табл. 4.2 також показано остаточний результат розв’язання задачі – оптимальний план перевезень вантажу поданий у вигляді виділених курсивом значень, що відповідає потокам на рис. 4.2, а на рис. 4.4 – результат розв'язання за допомогою Excel-таблиці У клітинках з вартістю, рівною нулю, потік є доповненням до пропускної здатності, тобто фіктивним.
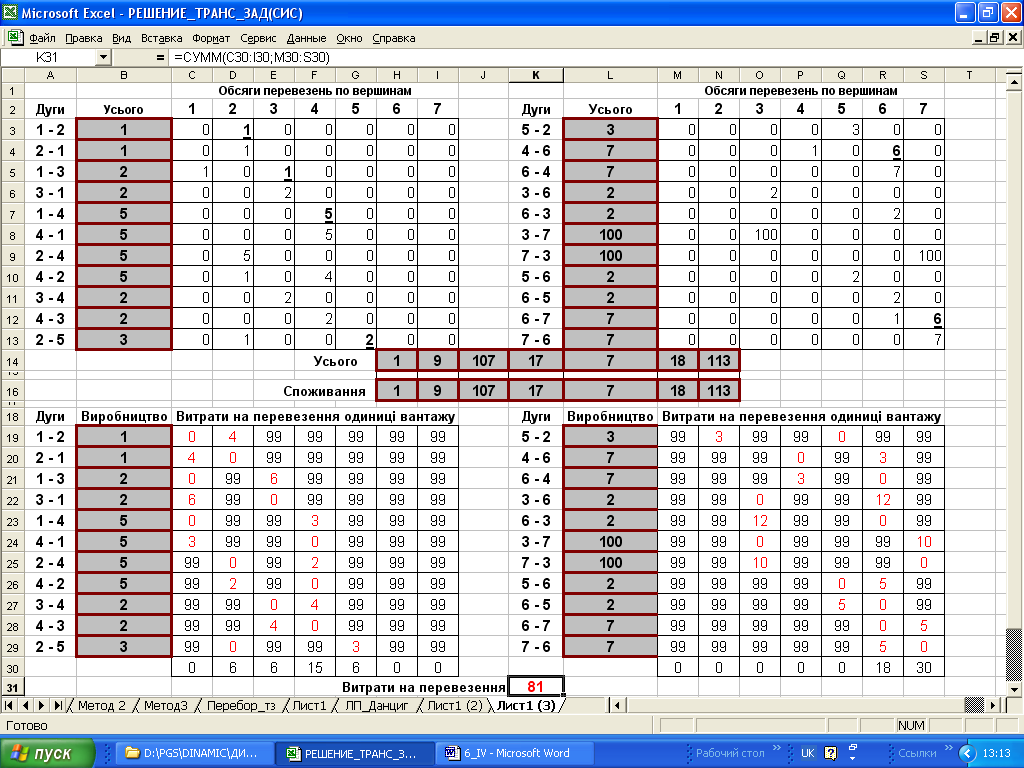
Рис. 4.4. Розв'язання мережевої ТЗ з обмеженнями на пропускні здатності за допомогою Excel-таблиці
