
- •12. Дискретные системы.
- •13. Импульсный элемент.
- •Теоремы z-преобразований.
- •Особенности дискретного преобразования Лапласа.
- •18. Устойчивость импульсных систем
- •Если хотя бы один корень zk располагается на окружности единичного радиуса, то система находится на границе устойчивости. При система неустойчива.
- •Критерий Гурвица.
- •Критерий Михайлова.
- •Критерий Найквиста.
- •20. Оценка качества импульсных систем
- •Параллельное программирование.
- •Метод последовательного программирования.
- •22.Уравнение переходных состояний для дискретно-непрерывных систем.
- •24. Цифровой регулятор, оптимальный по быстродействию
- •25. Метод переменного коэффициента усиления. Переменная е
- •26. Метод переменного коэффициента усиления. Переменная м
- •28. Нелинейные системы.
- •Типовые нелинейности
- •29. Типовая структурная схема нелинейных систем.
- •30. 31. Метод фазовых траекторий.
- •30. Метод фазовых траекторий для линейных систем.
- •33. Применение метода гармонической линеаризации для определения режима автоколебаний.
- •Критерий Гурвица для определения режима автоколебания.
- •Критерий Михайлова для определения режима автоколебания.
- •Критерий Найквиста.
- •35. Оценка абсолютной устойчивости нелинейных систем по Попову.
- •36. Понятие случайного процесса. Среднее значение сигнала, дисперсия .
- •37. Понятие случайного процесса.Корреляционная функция, спек тральная плотность.
- •Корреляционная функция
- •Спектральная плотность
- •38. Понятие случайного процесса. Взаимная корреляционная функция, спектральная плотность .
- •39. Типовые случайные воздействия
- •Случайное воздействия типа «белый шум»
- •Случайный ступенчатый сигнал
- •Случайный сигнал, имеющий скрытую периодическую составляющую
- •40. Преобразование случайного сигнала линейным звеном. Во временной области.
- •Преобразование сигнала во временной области
- •41. Преобразование случайного сигнала линейным звеном. В частотной области.
- •Преобразование случайного сигнала линейным звеном.
- •Преобразование сигнала во временной области
- •42. Преобразование сигнала в частотной области
- •42. Вычисление и минимизация дисперсии сигнала ошибки замкнутой системы
- •Методы идентификации систем автоматического управления Назначение и определение идентификации объектов
- •48. Адаптивные системы
- •Обобщенная схема адаптивной сау
- •Классификация адаптивных систем
- •49.Поисковые адаптивные сау
- •Метод Гаусса – Зейделя
- •Градиентный метод
- •Метод наискорейшего спуска
- •50. Беспоисковые адаптивные сау
Типовые нелинейности
Идеальное реле

Трехпозиционное реле или реле с зоной нечувствительностью

Двухпозиционное реле с гистерезисом

Трехпозиционное реле с гистерезисом

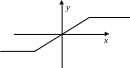
Нелинейность типа насыщения
Нелинейность типа насыщения с зоной нечувствительности

Усилитель с переменным коэффициентом усиления

Типа «идеальный диод»

Типа «модуль»
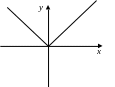
Типа «зазор» 11. Петля гистерезиса


29. Типовая структурная схема нелинейных систем.
Н аиболее
распространенная структурная схема
нелинейной системы имеет вид:
аиболее
распространенная структурная схема
нелинейной системы имеет вид:
где НЭ - нелинейный элемент;
ЛЧ – линейная часть
Рассмотрим уравнения этой системы, связывающее входной (r) и выходной (y) сигналы.
 (4.8)
(4.8)
Уравнение, связывающее входной и выходной сигнал нелинейного элемента (x и yН) имеет вид:
![]() (4.9)
(4.9)
ПРИМЕР
Пусть дана следующая нелинейная система :

Необходимо
ее преобразовать к типовому виду (Рис.
4.24). Для этого осуществляется перенос
первого сумматора на выход звена
![]()

З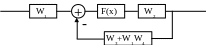 атем
объединяются две ветви обратной связи
атем
объединяются две ветви обратной связи
Далее система приводится к единичной обратной связи

Полученная нелинейная система отличается от типовой двумя дополнительными линейными звеньями: на входе и выходе системы. Линейное звено можно исключить из системы, заменив входной сигнал по формуле:
![]() (4.10)
(4.10)
А зная сигнал , можно получить выходной сигнал системы по выражению:
![]() (4.11)
(4.11)
Таким образом, для анализа свойств нелинейной системы можно ограничиться рассмотрением типовой схемы нелинейной системы (Рис. 4.24).
ПРИМЕР
Вывести уравнение, связывающее входной и выходной сигнал нелинейного элемента (x и yН)

Где
![]() ,
а нелинейный элемент – реле, имеющий
статическую характеристику
,
а нелинейный элемент – реле, имеющий
статическую характеристику
![]() :
:

![]() (4.12)
(4.12)
![]() (4.13)
(4.13)
Если входной сигнал – единичное ступенчатое воздействие, то (4.13) принимает вид
![]() (4.14)
(4.14)
30. 31. Метод фазовых траекторий.
Метод фазовых траекторий представляет собой графо-аналитический способ исследования нелинейных систем. Сущность метода заключается в описании поведения системы при помощи наглядных геометрических представлений – фазовых портретов.
Динамика
нелинейных систем с выходной переменной
![]() в общем случае описывается с помощью
нелинейного дифференциального уравнения:
в общем случае описывается с помощью
нелинейного дифференциального уравнения:
![]() (4.15)
(4.15)
Данное уравнение можно представить в виде системы нелинейных дифференциальных уравнений первого порядка:
![]() (4.16)
(4.16)
Переменные
![]() называются фазовыми
переменными состояния. Мгновенное
состояние системы и ее дальнейшее
поведение однозначно определено, если
в некоторый момент времени
называются фазовыми
переменными состояния. Мгновенное
состояние системы и ее дальнейшее
поведение однозначно определено, если
в некоторый момент времени
![]() известны значения всех
переменных
известны значения всех
переменных
![]() .
Эти значения можно рассматривать как
координаты точек
.
Эти значения можно рассматривать как
координаты точек
![]() в n-мерном
пространстве, которое называется фазовым
пространством.
в n-мерном
пространстве, которое называется фазовым
пространством.
Точку
с координатами
называют изображающей
точкой, а
линию, по которой она перемещается при
изменении состояния системы – фазовой
траекторией.
Известно, что конкретному начальному
состоянию системы
![]() соответствует
единственное решение системы (4.16), а
следовательно единственная фазовая
траектория. Поэтому множеству различных
начальных условий соответствует
семейство фазовых траекторий, которое
называется фазовым
портретом. Построение
фазового портрета дает нагляднее
представление о поведении системы, в
том числе предоставляет возможность
определить режим автоколебаний.
соответствует
единственное решение системы (4.16), а
следовательно единственная фазовая
траектория. Поэтому множеству различных
начальных условий соответствует
семейство фазовых траекторий, которое
называется фазовым
портретом. Построение
фазового портрета дает нагляднее
представление о поведении системы, в
том числе предоставляет возможность
определить режим автоколебаний.
Метод фазового пространства наиболее удобен для анализа систем второго порядка, так как их фазовые траектории располагаются в одной плоскости – в фазовой плоскости переменных x1 и x2. Фазовый портрет этих систем можно построить непосредственно по дифференциальному уравнению, не решая его.
Пусть описание системы представлено в виде дифференциального уравнения второго порядка:
![]() (4.17)
(4.17)
Данное уравнение можно представить в виде системы двух дифференциальных уравнений первого порядка
![]() , (4.18)
, (4.18)
где
![]() - отклонение выходной величины от
установившегося значения. В качестве
переменной
- отклонение выходной величины от
установившегося значения. В качестве
переменной
![]() принята производная переменной
принята производная переменной
![]() :
:
![]() .
Разделив второе уравнение системы
(4.18)
на первое,
можно получить уравнение фазовых
траекторий в дифференциальной форме:
.
Разделив второе уравнение системы
(4.18)
на первое,
можно получить уравнение фазовых
траекторий в дифференциальной форме:
![]() (4.19)
(4.19)
Решение данного дифференциального уравнения имеет уравнения фазовых траекторий в явном виде:
![]() , (4.20)
, (4.20)
где
![]() - постоянная интегрирования, зависящая
от начальных условий.
- постоянная интегрирования, зависящая
от начальных условий.
