22.Уравнение переходных состояний для дискретно-непрерывных систем.

Рассмотрим описание дискретно-непрерывной системы в течение интервала времени .

В первый момент (момент замыкания ключей ) система описывается с помощью матрицы ключей

. (49)

В момент между первым и вторым замыканием ключей, т. е. на интервале времени поведение системы описывается с помощью матрицы перехода

(3.50)

или

(3.51)

Введем матрицу - дискретную матрицу перехода. Тогда справедливо:

(3.52)

В момент замыкания ключей система описывается:

(3.53)

В момент между вторым и третьим замыканием ключей, т. е. на интервале времени поведение системы описывается:

(3.54)

Нетрудно заметить, что в момент времени поведение системы будет писываться следующим уравнением:

(3.55)

Данное уравнение называется уравнением переходных состояний и позволяет на основе известных матриц ключей и матрицы перехода в любой момент времени вычислить вектор состояния дискретно-непрерывной системы.

24. Цифровой регулятор, оптимальный по быстродействию

Пусть необходимо рассчитать цифровой регулятор, обеспечивающий переходный процесс конечной длительности . При это правомерно потребовать, чтобы длительность соответствовала порядку уравнения неизменяемой части си)стемы, который определяется главным образом объектом управления. Данное требование можно записать так :

,

где - порядок характеристического полинома приведенной части.

Условием получения конечной длительности переходного процесса является равенство всех (кроме первого) коэффициентов характеристического уравнения нулю:

. (3.107)

Тогда уравнение (3.106) с учетом (3.107) можно переписать:

Так как дискретная передаточная функция приведенной части известна, то дискретная передаточная функция регулятора определяется следующим образом:

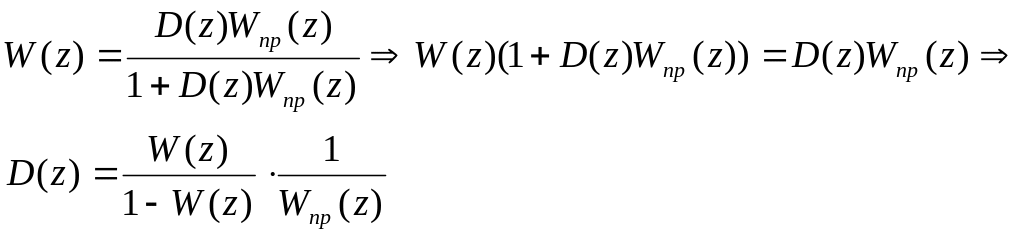
Полином числителя дискретной передаточной функции цифрового регулятора в данной задаче можно выбрать произвольным, например:

,

где - передаточный коэффициент регулятора;

- передаточный коэффициент приведенной части..

Тогда дискретная передаточная функция цифрового регулятора определится как:

В общем случае дискретная передаточная функция цифрового регулятора может быть записана как:

Соответственно уравнение для управляющего сигнала может быть записано как:

или

Выполнив обратное -преобразование, получаем:

Данное уравнение связывает текущее значение дискретного управляющего воздействия с текущим и предыдущими значениями ошибки, а также с предыдущими значениями управляющего воздействия. Данное уравнение называется разностным и может быть легко реализовано средствами вычислительной техники. Для реализации разностного уравнения требуется выполнение операций умножения, сложения и сдвига.

Рассмотренный метод обеспечивает оптимальный переходный процесс за счет выбора амплитуд управляющего воздействия на интервалах заданной продолжительности.

ПРИМЕР

Пусть непрерывная часть системы представлена последовательным соединением фиксирующего элемента и двух идеальных интегрирующих звеньев . Требуется рассчитать цифровой регулятор, обеспечивающий минимальную длительность переходного процесса при заданных значениях .=10 с и 0,01.

Дискретная передаточная функция приведенной системы имеет вид:

Характеристическое уравнение дискретной передаточной функции приведенной системы имеет порядок . Тогда можно определить и .

Оптимальная дискретная передаточная функция цифрового регулятора рассчитывается как:

Разностное уравнение имеет вид:

Рассчитанный цифровой регулятор обеспечивает окончание перехолного процесса за