
- •12. Дискретные системы.
- •13. Импульсный элемент.
- •Теоремы z-преобразований.
- •Особенности дискретного преобразования Лапласа.
- •18. Устойчивость импульсных систем
- •Если хотя бы один корень zk располагается на окружности единичного радиуса, то система находится на границе устойчивости. При система неустойчива.
- •Критерий Гурвица.
- •Критерий Михайлова.
- •Критерий Найквиста.
- •20. Оценка качества импульсных систем
- •Параллельное программирование.
- •Метод последовательного программирования.
- •22.Уравнение переходных состояний для дискретно-непрерывных систем.
- •24. Цифровой регулятор, оптимальный по быстродействию
- •25. Метод переменного коэффициента усиления. Переменная е
- •26. Метод переменного коэффициента усиления. Переменная м
- •28. Нелинейные системы.
- •Типовые нелинейности
- •29. Типовая структурная схема нелинейных систем.
- •30. 31. Метод фазовых траекторий.
- •30. Метод фазовых траекторий для линейных систем.
- •33. Применение метода гармонической линеаризации для определения режима автоколебаний.
- •Критерий Гурвица для определения режима автоколебания.
- •Критерий Михайлова для определения режима автоколебания.
- •Критерий Найквиста.
- •35. Оценка абсолютной устойчивости нелинейных систем по Попову.
- •36. Понятие случайного процесса. Среднее значение сигнала, дисперсия .
- •37. Понятие случайного процесса.Корреляционная функция, спек тральная плотность.
- •Корреляционная функция
- •Спектральная плотность
- •38. Понятие случайного процесса. Взаимная корреляционная функция, спектральная плотность .
- •39. Типовые случайные воздействия
- •Случайное воздействия типа «белый шум»
- •Случайный ступенчатый сигнал
- •Случайный сигнал, имеющий скрытую периодическую составляющую
- •40. Преобразование случайного сигнала линейным звеном. Во временной области.
- •Преобразование сигнала во временной области
- •41. Преобразование случайного сигнала линейным звеном. В частотной области.
- •Преобразование случайного сигнала линейным звеном.
- •Преобразование сигнала во временной области
- •42. Преобразование сигнала в частотной области
- •42. Вычисление и минимизация дисперсии сигнала ошибки замкнутой системы
- •Методы идентификации систем автоматического управления Назначение и определение идентификации объектов
- •48. Адаптивные системы
- •Обобщенная схема адаптивной сау
- •Классификация адаптивных систем
- •49.Поисковые адаптивные сау
- •Метод Гаусса – Зейделя
- •Градиентный метод
- •Метод наискорейшего спуска
- •50. Беспоисковые адаптивные сау
18. Устойчивость импульсных систем
Устойчивость
импульсных систем управления, как и
устойчивость непрерывной системы,
определяется характером ее свободного
движения. Импульсная система устойчива,
если свободная составляющая переходного
процесса
![]() с течением времени затухает, т. е. если
с течением времени затухает, т. е. если
![]() (3.56)
(3.56)
Свободная
составляющая
![]() является
решением однородного разностного
уравнения:
является
решением однородного разностного
уравнения:
![]() (3.57)
(3.57)
где
![]() - характеристическое уравнение,
представляющее знаменатель дискретной
передаточной функции:
- характеристическое уравнение,
представляющее знаменатель дискретной
передаточной функции:
 (3.58)
(3.58)
Решение уравнения (56) представляет собой сумму
![]() , (3.59)
, (3.59)
где
![]() - постоянные интегрирования, зависящие
от начальных условий;
- постоянные интегрирования, зависящие
от начальных условий;
![]() - корни характеристического уравнения
- корни характеристического уравнения
![]()
Из
выражения (59) видно, что при
![]() решение
стремится к нулю лишь в том случае, если
все корни
по модулю меньше единицы, т. е. если
решение
стремится к нулю лишь в том случае, если
все корни
по модулю меньше единицы, т. е. если
![]() (3.60)
(3.60)
Отсюда можно сформулировать общее условие устойчивости: для устойчивости импульсной системы необходимо и достаточно, чтобы все корни характеристического уравнения системы находились внутри круга единичного радиуса с центром в начале координат (рис. 3.34.).
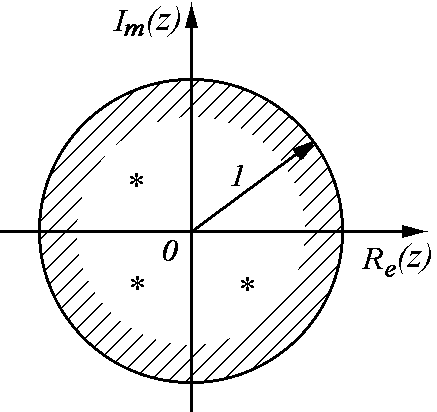
Рис. 3.34.
Если хотя бы один корень zk располагается на окружности единичного радиуса, то система находится на границе устойчивости. При система неустойчива.
19. Применение критериев устойчивости непрерывных систем для анализа устойчивости дискретных систем.
Критерий Гурвица.
Так, для того чтобы применить критерий Гурвица, необходимо предварительно в уравнении
![]()
произвести замену переменной z на переменную путем подстановки
![]()
и получить преобразованное характеристическое уравнение
![]()
Корням
уравнения (68), расположенным в плоскости
корней внутри единичного круга, теперь
будут соответствовать корни преобразованного
уравнения (70), находящиеся в плоскости
корней k
слева от мнимой оси (см. рис. 3.36.).
Действительно, если
![]() ,
то модуль числителя в выражении (69)
должен быть меньше модуля знаменателя,
т.е.
,
то модуль числителя в выражении (69)
должен быть меньше модуля знаменателя,
т.е.
![]() .
А это возможно лишь в том случае, если
вектор k
расположен в левой полуплоскости.
.
А это возможно лишь в том случае, если
вектор k
расположен в левой полуплоскости.
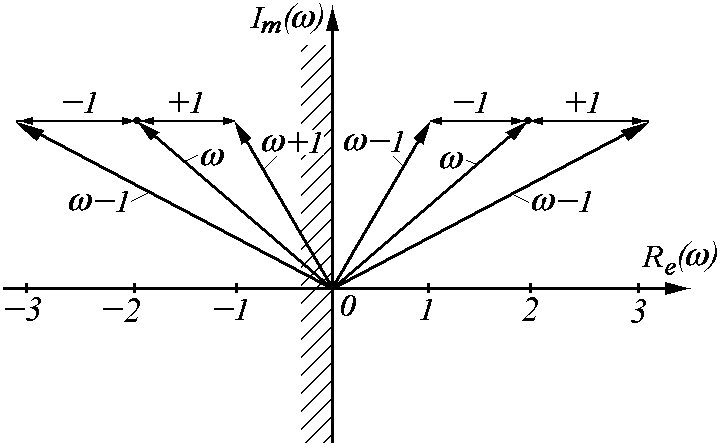
Рис. 3.36.
Критерий Михайлова.
При
использовании критерия Михайлова в
характеристический полином F(z)
подставляют
![]() ,
изменяют
от 0 до /Т
и в комплексной плоскости строят годограф
вектора F(ejT).
Импульсная система устойчива, если при
возрастании
от 0 до /Т
характеристический вектор F(ejT)
повернется против часовой стрелки на
угол п.
Если годограф характеристического
вектора проходит через начало координат,
то система находится на границе
устойчивости. Годографы вектора F(ejT)
для устойчивой и неустойчивой системы
второго порядка показаны на рисунке.
,
изменяют
от 0 до /Т
и в комплексной плоскости строят годограф
вектора F(ejT).
Импульсная система устойчива, если при
возрастании
от 0 до /Т
характеристический вектор F(ejT)
повернется против часовой стрелки на
угол п.
Если годограф характеристического
вектора проходит через начало координат,
то система находится на границе
устойчивости. Годографы вектора F(ejT)
для устойчивой и неустойчивой системы
второго порядка показаны на рисунке.

Рис. 3.37.
Критерий Найквиста.
Критерий Найквиста для импульсных систем формулируется также как и для непрерывных систем: система устойчива, если АФХ W(ejT) устойчивого разомкнутого контура не охватывает точку (-1; j0).
Характеристики устойчивой импульсной системы и неустойчивой системы, находящейся на границе устойчивости, показаны штриховыми линиями на рисунке.
Устойчивость разомкнутого контура импульсной системы определяется устойчивостью ее непрерывной части: если последняя устойчива, то и весь контур (включая импульсный элемент) устойчив.

Рис. 3.38.
