49.Поисковые адаптивные сау

Пусть дана исходная САУ и пределен критерий оптимальности как функция некоторых параметров , в качестве параметров могут быть рассмотрены как координаты объекта управления, так и задающие и управляющие воздействия.

Известно, что экстремальное значение критерия достигается при условии:

Однако часто аналитически это уравнения решить либо сложно, либо невозможно, поэтому нп практике применяются итерационные (численные) методы, обеспечивающие:

К итерационным методам относятся:

1. Метод Гаусса – Зейделя;

2. Градиентный метод;

3. Наискорейшего спуска

Метод Гаусса – Зейделя

В основе метода лежит исследование производной в точке экстремума

Метод Гаусса-Зейделя предполагает поочередное изменение и определение частных экстремумов при фиксировании всех остальных переменных. Такой цикл повторяется до нахождения экстремума по всем переменным с заданной точностью.

Пример

Пусть критерий оптимальности задан следующей формулой:

Необходимо найти минимум J при начальных значениях

Фиксируем переменную и находим частный экстремум по

Фиксируем переменную и находим частный экстремум по

И так далее до тех пор, пока

Градиентный метод

Состоит из двух этапов:

1. Делается пробный шаг по каждому из параметров x_i=x⁰_i+x;

2. Дапее осуществляется рабочий шаг в направлении градиента

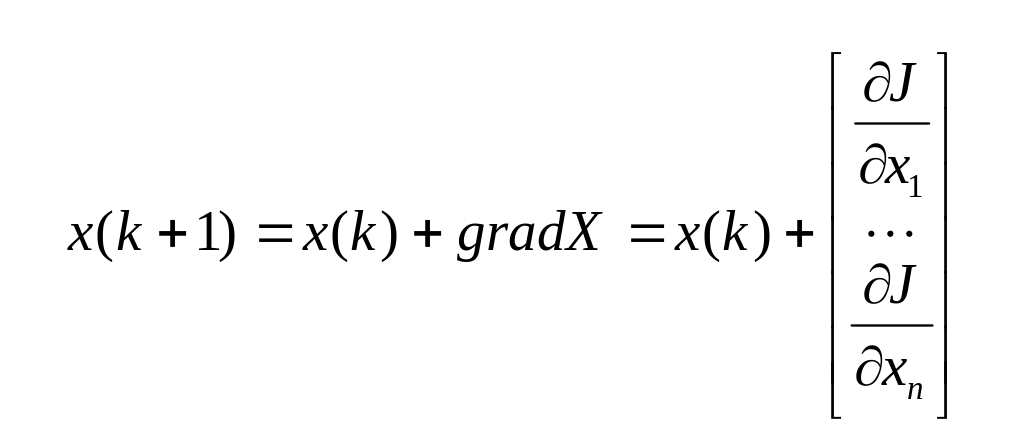
Далее повторяется первый этап и так далее, пока градиент:

не станет меьше заданной точности.

Метод наискорейшего спуска

Градиентный метод является модификацией градиентного метода. .Движение (поиск оптимального решения) продолжается до тех пор, пока J не перестанет уменьшаться.

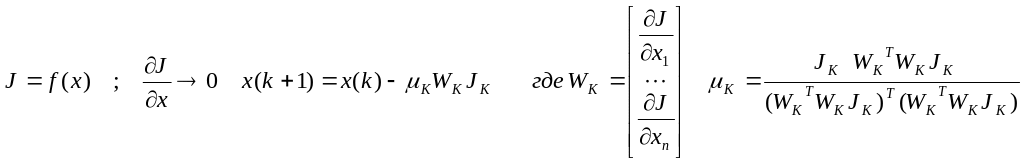
50. Беспоисковые адаптивные сау

В беспоисковых адаптивных САУ обеспечение экстремума может быть осуществлено следующими способами:

1. Предварительное аналитическое нахождение экстремума

и решение данного уравнения программно или аппаратно.

2. С использованием настраиваемой модели.

Процессы, протекающие в модели, являются оптимальными. Алгоритм адаптации осуществляет настройку регулятора таким образом, чтобы значение критерия качества было экстремально.

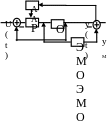
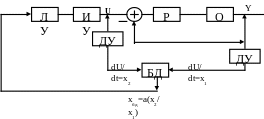
3. Беспоисковые САУ с вычислением производных

где

ЛУ - логическое устройство, определяющее воздействие, обеспечивающее экстремум критерия качества;

ИУ – исполнительное устройство;

ОУ – объект управления;

ДУ – дифференцирующее устройство;

БД – блок деления, обеспечивающий деление .

В системе с помощью ДУ осуществляется вычисление производных . На блоке деления получается сигнал . Логическое устройство ЛУ определяет задающее воздействие , обеспечивающее оптимальное управление объектом.