33. Применение метода гармонической линеаризации для определения режима автоколебаний.

Рассмотрим типовую нелинейную систему. Передаточная функция линейной части имеет вид:

(4.48)

Эквивалентную передаточную функцию нелинейного элемента можно получит из (47):

(4.49)

Тогда передаточная функция замкнутой системы имеет вид:

(4.50)

А характеристическое уравнение гармонически линеаризованной системы имеет вид:

(4.51)

Наиболее удобно исследовать автоколебания при помощи критерия Михайлова:

(4.52)

Согласно критерию устойчивости Михайлова в системе установятся колебания с постоянной амплитудой и частотой , если годограф Михайлова проходит через начало координат, т. е. когда и мнимая и действительная части характеристического полинома одновременно равны нулю:

(4.53)

Разрешая данную систему уравнений относительно , можно определить возможность возникновения автоколебаний в системе. Если уравнения (4.53) не имеют положительных корней , то автоколебания в системе невозможны.

Если положительные величины, то системе возможен режим колебания с постоянной амплитудой. Определить, являются ли данные колебания автоколебаниями, можно с помощью дополнительных исследований.

Изучая фазовые траектории, соответствующие режиму автоколебаний, можно сделать следующий вывод: что в режиме автоколебаний при увеличении амплитуды на величину в системе происходил сходящийся процесс к величине ; а при уменьшении на происходил расходящийся процесс до величины . Аналогичные процессы происходят при изменении частоты .

Для дополнительных исследований на устойчивость колебаний применяются критерии устойчивости: Гурвица, Михайлова и Найквиста.

Критерий Гурвица для определения режима автоколебания.

Для того чтобы колебания были устойчивыми по Гурвицу необходимо выполнение следующих условий:

• предпоследний определитель матрицы Гурвица должен быть равен нулю:

(4.54)

• все определители Гурвица, для характеристического уравнения нелинейной системы после гармонической линеаризации при увеличении амплитуды входного сигнала, должны оставаться положительными:

(4.55)

• все определители Гурвица, кроме двух последних, при уменьшении амплитуды входного сигнала должны быть отрицательными:

(4.56)

Аналогично критерий Гурвица применяется и для частоты .

Критерий Михайлова для определения режима автоколебания.

По критерию Михайлова выполнение нижеприведенного неравенства означает возможность режима автоколебаний:

>0 (4.57)

Если линейная часть описывается уравнением высокого порядка или содержит звено чистого запаздывания, то применение критерия становится затруднительным, и тогда применяют критерий Найквиста.

Критерий Найквиста.

Согласно критерию Найквиста система находится на колебательной границе устойчивости, если амплитудно-фазовая характеристика разомкнутого контура проходит через точку . Следовательно, условием существования автоколебаний является равенство:

(4.58)

или

(4.59)

Левая часть уравнения (4.59) представляет собой АФХ линейной части, а правя – обратную характеристику нелинейного элемента, взятую с противоположным знаком.

Уравнение (4.59) можно решить графически. Строится два графика , точки пересечения этих графиков определяют режимы колебаний с постоянной амплитудой и частотой.

Для определения режима автоколебаний пользуются следующим правилом:

Если точка на графике , близкая к точке пересечения, но сдвинутая в сторону увеличения параметра не охватывается графиком , то колебания являются устойчивыми, в противном случае – неустойчивыми.

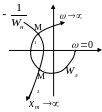
Рис. 4.49.

На рисунке точка М₁ соответствуют режиму автоколебаний, а М₂ – неустойчивым колебаниям.

34. Метод припасовывания.

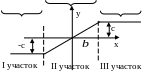
Этот метод применяется для нелинейных систем управления, нелинейные элементы которых имеют кусочно-линейную или кусочно постоянную статическую характеристику.

Отрезки кусочно-линейной характеристики определяют количество участков, которые и участвуют в процедуре припасовывания. Метод припасовывания является точным методом решения конкретного уравнения, но трудоемок в вычислениях, которая возрастает с увеличением порядка линейной части и сложностью нелинейной характеристики.

Алгоритм метода припасовывания:

1. Составляются уравнения, описывающие нелинейную систему на каждом из участков нелинейной характеристики;

2. Для каждого из участков решаются в общем виде линейные уравнения;

3. По заданным начальным условиям и входному воздействию, определяется участок, с которого начинается переходный процесс. С учетом данных условий вычисляются произвольные постоянные, входящие в общее решение уравнения;

4. Решается уравнение для граничного значения данного участка линейной характеристики;

5. Повторяются п.3, 4.

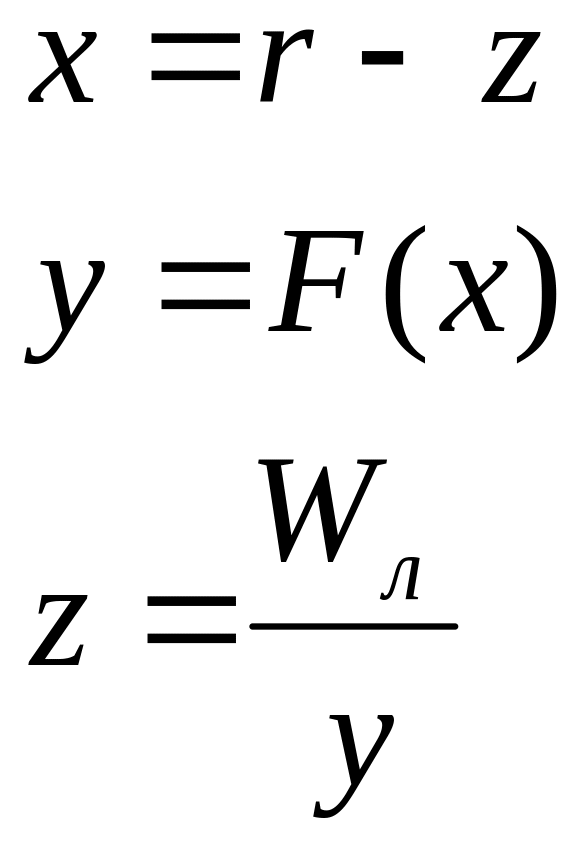(4.62)

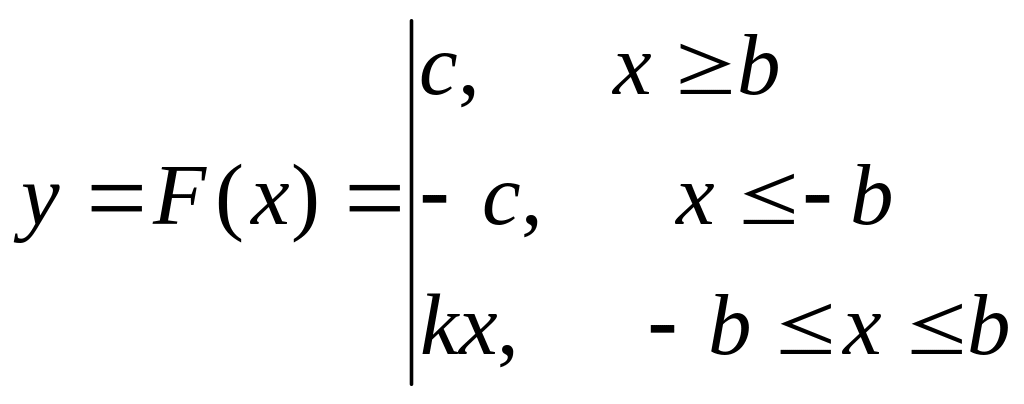(4.63)

I участок:

II участок:

III участок:

Начальные условия:

.