
- •12. Дискретные системы.
- •13. Импульсный элемент.
- •Теоремы z-преобразований.
- •Особенности дискретного преобразования Лапласа.
- •18. Устойчивость импульсных систем
- •Если хотя бы один корень zk располагается на окружности единичного радиуса, то система находится на границе устойчивости. При система неустойчива.
- •Критерий Гурвица.
- •Критерий Михайлова.
- •Критерий Найквиста.
- •20. Оценка качества импульсных систем
- •Параллельное программирование.
- •Метод последовательного программирования.
- •22.Уравнение переходных состояний для дискретно-непрерывных систем.
- •24. Цифровой регулятор, оптимальный по быстродействию
- •25. Метод переменного коэффициента усиления. Переменная е
- •26. Метод переменного коэффициента усиления. Переменная м
- •28. Нелинейные системы.
- •Типовые нелинейности
- •29. Типовая структурная схема нелинейных систем.
- •30. 31. Метод фазовых траекторий.
- •30. Метод фазовых траекторий для линейных систем.
- •33. Применение метода гармонической линеаризации для определения режима автоколебаний.
- •Критерий Гурвица для определения режима автоколебания.
- •Критерий Михайлова для определения режима автоколебания.
- •Критерий Найквиста.
- •35. Оценка абсолютной устойчивости нелинейных систем по Попову.
- •36. Понятие случайного процесса. Среднее значение сигнала, дисперсия .
- •37. Понятие случайного процесса.Корреляционная функция, спек тральная плотность.
- •Корреляционная функция
- •Спектральная плотность
- •38. Понятие случайного процесса. Взаимная корреляционная функция, спектральная плотность .
- •39. Типовые случайные воздействия
- •Случайное воздействия типа «белый шум»
- •Случайный ступенчатый сигнал
- •Случайный сигнал, имеющий скрытую периодическую составляющую
- •40. Преобразование случайного сигнала линейным звеном. Во временной области.
- •Преобразование сигнала во временной области
- •41. Преобразование случайного сигнала линейным звеном. В частотной области.
- •Преобразование случайного сигнала линейным звеном.
- •Преобразование сигнала во временной области
- •42. Преобразование сигнала в частотной области
- •42. Вычисление и минимизация дисперсии сигнала ошибки замкнутой системы
- •Методы идентификации систем автоматического управления Назначение и определение идентификации объектов
- •48. Адаптивные системы
- •Обобщенная схема адаптивной сау
- •Классификация адаптивных систем
- •49.Поисковые адаптивные сау
- •Метод Гаусса – Зейделя
- •Градиентный метод
- •Метод наискорейшего спуска
- •50. Беспоисковые адаптивные сау
12. Дискретные системы.
Дискретные системы – это системы, в которых хотя бы в одном из звеньев непрерывному входному сигналу соответствует дискретный выходной сигнал. Преобразование непрерывного сигнала в дискретный называется квантованием, или дискретизацией. Звено, в котором происходит дискретизация сигнала, называется квантователем или дискретным элементом.
Виды
квантования:
1.по
уровню (пример: релейные системы)
заключается в фиксации вполне определенных
дискретных значений непрерывного
сигнала. При этом непрерывный сигнал
заменяется ступенчато изменяющимся
сигналом. Смежные дискретные значения
отличаются друг от друга
![]() ,
называемую шагом
квантования.
Переход от одного уровня квантования
на другой происходит в моменты времени,
когда непрерывный сигнал достигает
очередного фиксированного значения.
,
называемую шагом
квантования.
Переход от одного уровня квантования
на другой происходит в моменты времени,
когда непрерывный сигнал достигает
очередного фиксированного значения.

(1)
2.по
времени (пример: импульсные сист.)
заключается
в фиксации значений непрерывного сигнала
в равноотстоящие друг от друга дискретные
моменты времени. При этом квантованный
сигнал представляет собой последовательность
импульсов. Смежные моменты времени
отличаются на постоянную величину
![]() ,
называемую интервалом
дискретности или шагом дискретности.
,
называемую интервалом
дискретности или шагом дискретности.

(2) (3)
3.по уровню и по времени (пример: цифровые сист.) фиксируются дискретные по уровню значения в дискретные моменты времени.
Квантование по уровню в релейных системах осуществляется при помощи специальных элементов – квантователей. Простейшими квантователями являются двух- и трехпозиционные реле.


Квантование по времени осуществляется с помощью импульсного элемента. Импульсный элемент преобразует непрерывный входной сигнал в последовательность равноотстоящих друг от друга импульсов.
13. Импульсный элемент.
Импульсный элемент преобразует непрерывный входной сигнал в последовательность равноотстоящих друг от друга импульсов. Основными параметрами импульса являются:
амплитуда импульса (высота импульса)
 ;
;длительность импульса (ширина импульса)
 ;
;расположение импульса внутри интервала квантования
 .
.

Рис. 3.6.
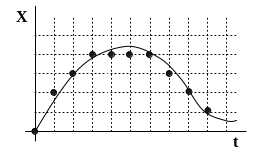
В зависимости от того, какой из параметров импульса меняется в процессе модуляции, различают следующие виды модуляции: 1) При амплитудно-импульсной модуляции изменяется амплитуда импульса в зависимости от значения непрерывного сигнала в момент квантования, остальные параметры остаются неизменными.

Рис. 3.7.

2) При широтно-импульсной модуляции изменяется длительность импульса в зависимости от значения непрерывного сигнала в момент квантования, остальные параметры остаются неизменными.

Рис. 3.8.
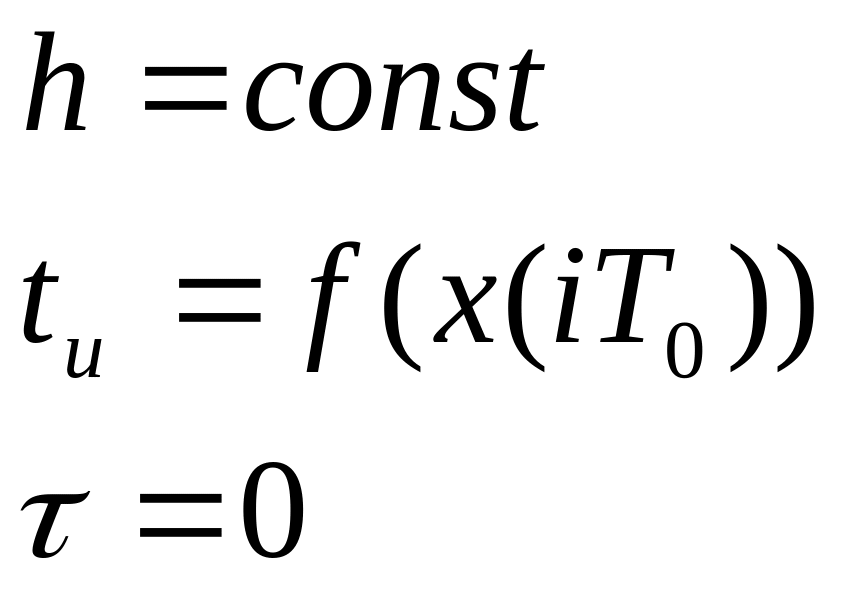
3) При временно-импульсной модуляции изменяется положение импульса внутри интервала квантования в зависимости от значения непрерывного сигнала в момент квантования, остальные параметры остаются неизменными.

Рис. 3.9.
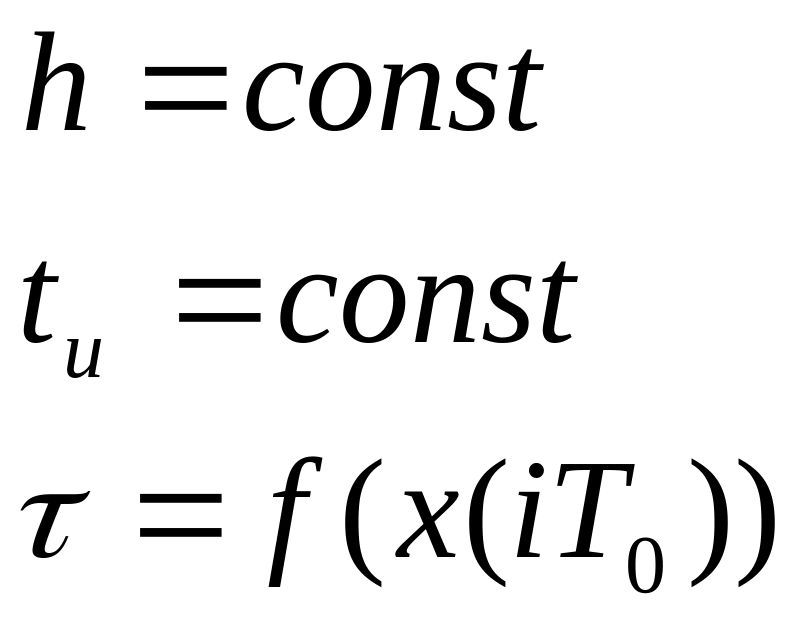
Импульсный
элемент можно рассматривать как ключ,
который замыкается через каждые
![]() секунд на бесконечно малый отрезок
времени
секунд на бесконечно малый отрезок
времени
![]() .
.
![]()
Рис. 3.10.
14. Фиксирующий элемент
Цифровые системы управления строятся по следующему принципу:

Рис. 3.20.
Где
ЦР – цифровой регулятор, представленный
дискретной передаточной функцией
![]() ;
;
Ф- фиксатор или фиксирующий элемент;
![]() -
передаточная функция непрерывной части.
-
передаточная функция непрерывной части.
Функции
цифрового регулятора и фиксирующего
элемента реализуются с помощью
вычислительных средств. Задача
фиксирующего элемента преобразовать
цифровую информацию в непрерывный
сигнал, которым можно воздействовать
на последующую непрерывную часть системы
управления. Обычно желательно, чтобы
сигнал после фиксатора
![]() представлял
собой огибающую для последовательности
импульсов , то. Е. в интервале
представлял
собой огибающую для последовательности
импульсов , то. Е. в интервале
![]() фиксатор дожжен экстраполировать
значение амплитуды сигнала в момент
фиксатор дожжен экстраполировать
значение амплитуды сигнала в момент
![]() на весь i-тый
интервал. Отсюда второе название
фиксатора как экстраполятор
m-го
порядка.
Экстраполятор m-го
порядка реализует полиномиальную
экстраполяцию:
на весь i-тый
интервал. Отсюда второе название
фиксатора как экстраполятор
m-го
порядка.
Экстраполятор m-го
порядка реализует полиномиальную
экстраполяцию:
![]() (3.32).
(3.32).
Коэффициенты
![]() на основе амплитуд сигналов в предыдущие
моменты времени.
на основе амплитуд сигналов в предыдущие
моменты времени.
На практике широкое распространение получили экстраполяторы первого и нулевого порядка.
Экстраполятор первого порядка описывается полином первого порядка:
![]() (3.33).
(3.33).
Коэффициенты
![]() определяются следующим образом:
определяются следующим образом:
![]() (3.34)
(3.34)
Сигнал экстраполятор первого порядка представлен на рис:
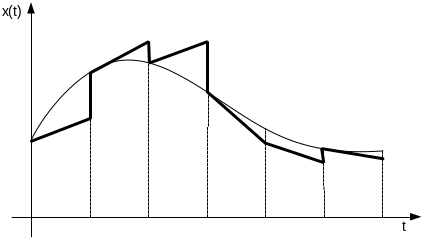
Рис. 3.21.
Экстраполятор нулевого порядка описывается полином нулевого порядка:
![]() (3.35).
(3.35).
Коэффициент
![]() определяется следующим образом:
определяется следующим образом:
![]() (3.36)
(3.36)
Сигнал экстраполятор нулевого порядка представлен на рис:
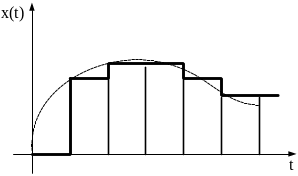
Рис. 3.22.
Очевидно, что с точки зрения реализации предпочтительность имеет экстраполятор нулевого порядка. Передаточная функция экстраполятора нулевого порядка:
![]() (3.37)
(3.37)
Дискретная функция импульсной системы с фиксатором (рис.3.23.) определяется следующим образом:
![]()
![]() (3.38)
(3.38)
![]()
Рис. 3.23.

Рис. 3.24.
Р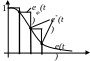 ассмотрим
преобразование непрерывного сигнала
при прохождении через импульсную
систему, а именно через последовательное
соединение импульсного элемента (ключа)
и фиксирующего элемента (экстраполятор
нулевого порядка) (рис. 3.25.) .
ассмотрим
преобразование непрерывного сигнала
при прохождении через импульсную
систему, а именно через последовательное
соединение импульсного элемента (ключа)
и фиксирующего элемента (экстраполятор
нулевого порядка) (рис. 3.25.) .

Рис. 3.25. Рис. 3.26.
15. Решетчатая функция.
Решетчатая
функция – функция,
которую образуют ординаты непрерывной
функции при дискретных равноотстоящих
друг от друга значениях независимой
переменной. Решетчатая функция существует
только при дискретных значениях
аргумента. То есть для описания импульсной
системы с амплитудной модуляцией
наилучшим образом подходит решетчатая
функция. При этом непрерывный сигнал
![]() импульсным элементом преобразуется в
последовательность импульсов
импульсным элементом преобразуется в
последовательность импульсов
![]() ,
то есть в решетчатую функцию. Непрерывная
функция
является огибающей для решетчатой
функции
,
то есть в решетчатую функцию. Непрерывная
функция
является огибающей для решетчатой
функции
![]() .
Введем понятие единичного импульса
.
Введем понятие единичного импульса
![]() ,
тогда последовательность неединичных
импульсов может быть представлена в
следующем виде:
,
тогда последовательность неединичных
импульсов может быть представлена в
следующем виде:
![]() (3.6)
(3.6)
Изображение Лапласа для i-того неединичного импульса имеет вид:
![]() (3.7)
(3.7)
Так
как для каждого фиксированного значения
i
величина
![]() ,
то ее можно вынести за знак интеграла.
Согласно теореме запаздывания изображение
смещенной
,
то ее можно вынести за знак интеграла.
Согласно теореме запаздывания изображение
смещенной
![]() -функции
равно
-функции
равно![]() .
Тогда выражение (7) можно переписать:
.
Тогда выражение (7) можно переписать:
![]()
Тогда изображение по Лапласу всей последовательности импульсов равно :
![]()
![]() (3.9)
(3.9)
Выражение
(9) называется дискретным
преобразованием Лапласа. Оно
устанавливает соответствие между
решетчатыми функциями и их изображениями.
Введя новую перемену.
![]() ,
можно получить так называемое
z-преобразование:
,
можно получить так называемое
z-преобразование:
![]() (3.10)
(3.10)
Таким образом, математически преобразование непрерывного сигнала в дискретный сигнал осуществляется следующим образом:
непрерывный сигнал заменяется последовательностью импульсов (решетчатая функция).
к решетчатой функции применяется z-преобразование

степенной ряд сворачивается в конечную сумму. Это конечная сумма и представляет собой дискретные преобразования Лапласа
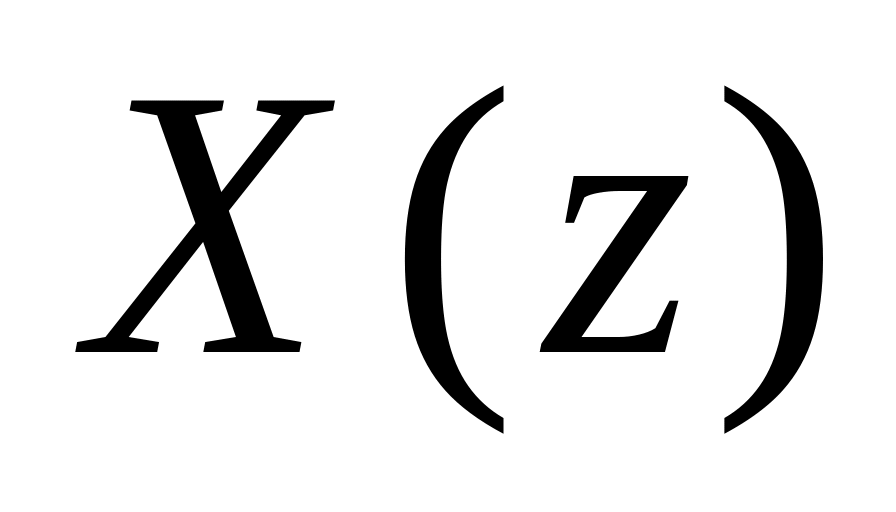 .
.
Пример
Получить
Z-преобразование
функции
![]() .
.
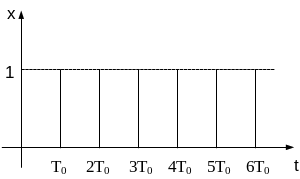
Рис. 3.11.
Решетчатая функция имеет вид

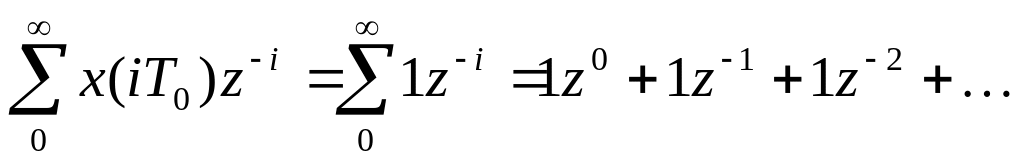
Конечная сумма ряда:
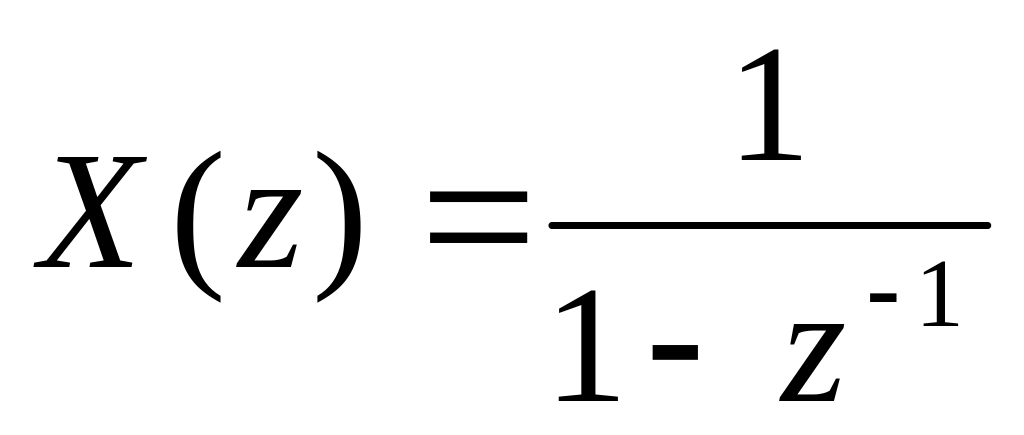
Для большинства встречающихся в задачах решетчатых функций z-преобразование может быть выполнено при помощи таблиц соответствия, которые приводятся в специальной литературе по импульсным системам.
Свойства z-преобразования аналогичны свойствам обычного преобразования. Приведем важнейшие из них.
