Необходимое и достаточное условие существования предела функции. Теорема о представлении функции, имеющей предел:

Для того чтобы число А было пределом функции f(x) при xx₀ , необходимо и достаточно, чтобы в некоторой окрестности точки x₀ f(x) была представима следующим образом: f(x)=A+(x), где (x) – б/м при _.

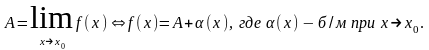
Док-во:

Необходимость. Пусть

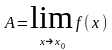
    из |x-x₀| < следует неравенство |f(x)-A| < _.

Это неравенство означает, что f(x)–A=(x) ‒ б/м при xx₀ (по определению б/м). Отсюда f(x)=A + (x).

Достаточность. В некоторой окрестности точки x₀ функция представима в виде: f(x) = A+(x), где (x) – б/м при xx₀.  (x)=f(x)–A – б/м, то есть по определению:     из неравенства |x-x₀| < |f(x) – A|< .

Последнее неравенство означает, что .

Ч.т.д.

Арифметические операции с пределами.

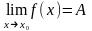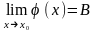Теорема 1: Пусть , а , тогда

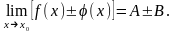
Док-во: По теореме о представлении функций, имеющих предел: f(x)=A+(x), где (x) – б/м при x®x₀, а  (x)=B+(x), где (x) ‒ б/м при xx₀.

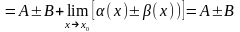
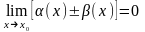, как сумма двух б/м.

Ч.т.д.

Теорема 2: Пусть , а , тогда .

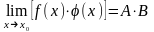Док-во: По теореме о представлении функций, имеющих предел: f(x)=A+a(x), где a(x) – б/м при x®x₀, а j (x)=B+b(x), где b(x) ‒ б/м при x®x₀.

f(x)· (x)= (A(x))·(B+(x))=A·B+A·(x)+ (x)·B+ (x)·(x)=A·B, так как A·(x) и (x)·B и (x)·(x) стремятся к нулю при xx₀ по свойствам б/м. Переходя к пределу при xx₀ получаем требуемое.

Ч.т.д.

Теорема 3: Пусть , а , тогда 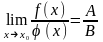, где B0.

Доказывается теорема аналогично теоремам 1 и 2.

Следствие: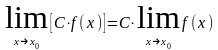 , где C-const.

Неопределенности. Если не применимы основные теоремы о пределах, свойства б/м и б/б, то возникают неопределенности вида: ,  · ^ ⁰), (⁰), ().

Рассмотрим три вида неопределенности: , (), .

Пример. Вычислить пределы.

1) = =

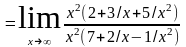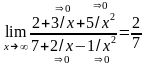
2)

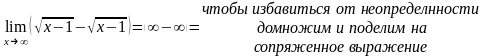
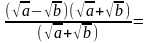
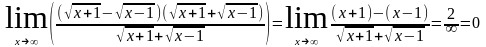
3)

от неопределенности избавимся следующим образом: разложим числитель и знаменатель на множители и сократим.

4)

чтобы избавиться от иррациональности, надо умножить и поделить на сопряженное выражение.

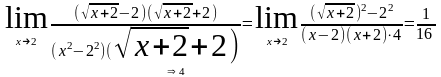
Теоремы о предельном переходе в неравенствах.

Теорема 1. Теорема о «двух милиционерах».

Пусть заданы 3 функции f(x), j(x), g(x) такие, что f(x)£j(x)£g(x). Тогда если

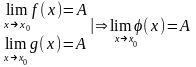
Док-во: Вычтем А из всех частей неравенства f(x)£j(x)£g(x):

f(x)-A£j(x)-A£g(x)-A.

По теореме о представлении функции, имеющей предел: f(x)=A+a(x), g(x)=A+b(x), где a(x) и b(x) являются б/м. Между двумя б/м может находиться только б/м Þ по теореме о представлении функции, имеющей предел: .

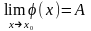Ч.т.д.

Теорема 2: Пусть функция f(x)³0 и существует конечный предел 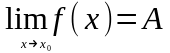. Тогда A³0.

Док-во: Предположим противное: A<0. Тогда окрестность точки A лежит по оси ОY ниже начала координат. Þ В этой окрестности f(x)<0, чего быть не может.

Ч.т.д.

Т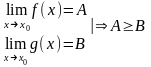 еорема 3: Если f(x)³g(x) и

Док-во: Из неравенства f(x)³g(x) Þ f(x)-g(x)³0. По предыдущей теореме и арифметическим операциям Þ A³B.

Ч.т.д.

Первый замечательный предел.

Доказательство:

Рассмотрим единичную окружность и отложим бесконечно малый угол x.

П усть 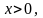т.е. принадлежит 1 четверти.

Очевидны следующие неравенства:

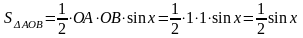
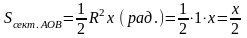
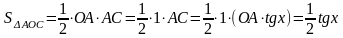
Вернемся к неравенствам:

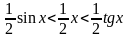
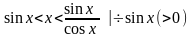
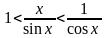
Перейдем к обратным выражениям:

Левая часть неравенства 1 1, т.к.

Правая часть неравенства

По теореме «о двух милиционерах»:

Аналогично при х<0:

Вместо x может быть любая б/м при х х₀, тогда

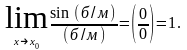
Ч.т.д.

Пример:

1)

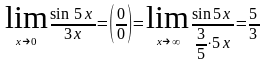
2)

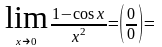
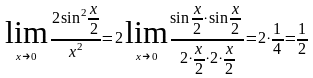
3)