Предел функции.

Пусть функция y=f(x) определена в некоторой окрестности точки a, за исключением, может быть самой точки.

1) Определение предела функции на языке :

Число А называется пределом функции f(x) при xa, если для любого сколь угодно малого положительного числа  найдется число (e)>0 такое, что для всех x, отличных от a и удовлетворяющих неравенству |x-a|<, следует неравенство |f(x)-A|<.

 >0 >0: из |x-a|<  |f(x)-А|<.

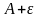
y

A

х

x₁

х

x₁

a

a+δd

a-

Интервал (a-, a+) на оси ОХ называется дельта-окрестностью точки a.

Интервал (A-, A+) на оси ОY называется эпсилон-окрестностью точки A.

Функция y=f(x) переводит каждую точку из -окрестности точки a на оси ОХ внутрь ε-окресности точки А на оси ОY.

2) Определение предела на языке окрестности:

Число A называется пределом функции при xa, если для любой сколь угодно малой -окрестности точки A на оси ОY найдется -окрестность точки a на оси ОХ, которую функция переводит в -окрестность.

3) Определение предела на языке последовательности:

Число A называется пределом функции f(x) при xa, если для любой последовательности {x_n}, сходящейся к точке a, соответствующая последовательность значений функции {f(x_n)} сходится к A.

4) Правый и левый пределы.

Определение: Если есть x_na и x_n<a, то число A называется левым пределом функции при xa-0.

.

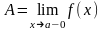Определение: Если x_na и x_n>a, то число A называют правым пределом функции при xa+0.

.

Такие пределы называются односторонние.

Замечание 1: Для существования предела функции не требуется, чтобы функция была определена в самой точке x=a, достаточно того, что она определена в ее окрестности.

Замечание 2: На последовательность {x_n} можно смотреть как на функцию натурального аргумента x_n=f(n), nN. Поэтому все свойства пределов и теоремы для пределов функции справедливы и для предела последовательности.

Единственность предела функции.

Теорема: Если функция имеет предел при xa, то он единственен.

Док-во: Предположим противное. Пусть у функции существуют два предела при xa и 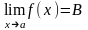. Возьмем >0 так, чтобы окрестности точек A и B не пересекались. По определению предела функции: существует такое >0, что из |x-a|< следует |f(x)-A|<, |f(x)-B|<, т.е. значения f(x) лежат одновременно в -окрестности точки A и -окрестности точки B, чего быть не может, т.к. окрестности не пересекаются, полученное противоречие доказывает теорему.

Ч.т.д.

Бесконечно малые и бесконечно большие функции. Иx свойства.

Определение: Функция (x) называется бесконечно малой при xx₀, если .

Обозначается (x) – б/м при xx₀.

Функция (x) – б/м при xx₀, если    из xx₀   х .

Определение: Функция y=f(x) называется ограниченной, если существует такое число  >0, что |f(x)| М при  .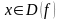

Определение: Функция f(x) называется бесконечно большой при x®x₀, если .

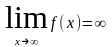Обозначается f(x) ‒ б/б при x®x₀.

Функция f(x) ‒ б/б при x®x₀, если для любого А0 найдется >0: из неравенства |x-x₀|< следует неравенство |f(x)|>А.

В качестве x₀ может быть конечное число,  или .

Свойства.

1. Сумма двух или конечного числа б/м есть бесконечно малая.

2. Произведение двух или конечного числа б/м есть бесконечно малая.

3. Произведение б/м на ограниченную функцию есть б/м.

Замечание: Частное двух б/м является неопределенностью вида .

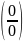4. Сумма конечного числа б/б есть б/б.

5. Произведение конечного числа б/б есть б/б.

6. Произведение б/б на любую не б/м есть б/б.

Замечание: Разность двух б/б является неопределенностью вида (-).

Замечание: Частное двух б/б является неопределенностью вида .

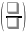Замечание: Произведение б/б на б/м является неопределенностью вида .

7. Частное от деления б/б на ограниченную функцию есть б/б.

8. Б/м и б/б ‒ взаимообратные функции.

Док-во:

1) б/м есть обратная величина для б/б. .

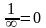Пусть f(x) – б/б при xx₀. Тогда по определению б/б: для любого A>0 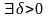такое, что из неравенства |x-x₀| < будет следовать неравенство |f(x)| >A. Перейдем к обратным величинам: |1/f(x)| < 1/A Þ б/м по определению.

2) б/б есть обратная величина для б/м.

Пусть (x) – б/м при xx₀. Тогда по определению:     такое, что из неравенства |x-x₀|<  неравенство |(x)|< . Перейдем к обратным величинам: |1/(x)| > 1/ , что означает по определению, что 1/(x) – б/б величина.

Ч.т.д.