Скалярное произведение векторов.

Определение: Скалярным произведением двух векторов называется число равное произведению длин этих векторов (модулей) на косинус угла между векторами.

По определению: a • b= │a│·│b│· cos φ.

, .

, .

- связь между скалярным произведением и проекцией вектора на вектор.

Свойства скалярного произведения.

1° коммутативность: a • b = b •· a.

a • b= │a│·│b│· cos φ= │b│·│a│· cos φ= b • a.

2° условие перпендикулярности: a • b= 0, т.к. a _┴ b или a или b= 0.

1. a _┴ b, φ= 90°, cos 90°= 0, a • b= │a│·│b│·0= 0.

2. a= 0, │a│= 0, a • b= 0 ·│b│· cos φ= 0.

3° (λa)•b= λ(a•b).

(λa)•b= │λa│·│b│· cos φ=λ│a│·│b│· cos φ= λ(a•b).

4° a•(b + c)= a•b + a•c.

a•(b + c)= │a│· (b + c)= │a│·( пр_а b + пр_а c)= │a│·пр_а b +│a│· пр_а c=

= a•b + a•c.

5° скалярный квадрат: а • а= │a│².

а • а=│a│·│а│· cos 0°=│a│².

Следствие: _.

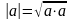Пример. Пользуясь определением скалярного произведения и его свойствами вычислить a • b, │a│, если, а= 2p - q, b= p + 3q, где │p│=2, │q│=3,

φ= p;q= _.

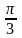Скалярное произведение координатных ортов.

i  j= 0, так как i  j (из 2);

i  k= 0, так как i  k (из 2);

k  j= 0, так как k  j (из 2);

i  i=│i│² = 1²=1;

j  j=│j│² = 1²=1;

k  k=│k│² = 1²=1.

Скалярное произведение в координатной форме. Возьмем два вектора в координатной форме

а= (а_х, а_у, а_z)= a_xi + a_yj + a_zk, b= (b_x, b_y, b_z)= b_xi + b_yj + b_zk.

a • b= (a_xi + a_yj + a_zk )•( b_xi + b_yj + b_zk)= a_xi•b_xi + a_xi•b_yj + a_xi •b_zk + a_yj• b_xi +

+ a_yj• b_yj + a_yj •b_zk + a_zk •b_xi + a_zk•b_yj + a_zk •b_zk = a_x b_x i• i + a_x b_y i•j + a_x b_z i•k+

+a_y b_x i• j + a_y b_y j• j + a_y b_z i• k + a_z b_x i•k + a_z b_y k• j + a_z b_z k•k=

= a_x b_x + a_y b_y + a_z b_z.

Если векторы заданы в координатной форме, то для вычисления скалярного произведения используем формулу:

a • b= a_x b_x + a_y b_y + a_z b_z.

Приложения скалярного произведения.

1. Угол между векторами:

.

 - острый, cos > 0, отсюда следует, что a • b> 0.

 - тупой, cos < 0, отсюда следует, что a • b< 0.

= 90, cos = 0, отсюда следует, что a • b= 0.

2. Проекция вектора на вектор:

.

Пример. Дан треугольник АBС, т. A(2, -1, 3), т. B(4, 0, 1), т. С(-1, 3, 0). Найти угол А, пр_AC AB-?

Векторное произведение двух векторов.

Определение: Векторным произведением ab векторов a и b называется третий вектор с, обладающий следующими свойствами:

1 │с│=│a│·│b│·sin φ, где = a,b;

2 вектор c  a, c b, т.е. с  плоскости, в которой лежат вектора а и b;

3 кратчайший поворот от вектора a к b, видимый с конца вектора с будет против часовой.

Свойства векторного произведения:

1 антикоммутативность: ab= - ba.

ab= с, ba= -с.

2 (λa)b= λ (ab).

3 a(b + с)= ab + aс.

4 a  а= 0.

│ a  а │=│a│·│а│sin 0°= 0. Отсюда следует, что a  а= 0.

Векторные произведения координатных ортов.

i

k

Если первый орт умножить векторно на второй орт, то по стрелке получим третий орт, причем взятый с «+», если поворот против часовой стрелки, и берется с «-», если по часовой стрелке.

ij= k,

ik= -j,

jk= i,

ji= -k,

ii= 0.