Евклидово пространство.
Определение: Линейное пространство называется евклидовым, если в нем введена операция скалярного произведения, которая ставит в соответствие любым векторам х и у Є L число x•y, удовлетворяющее следующим свойствам:
1° x•y=y•x;
2° (lx)• y= l(x•y);
3° x•(y + z)= x•y + x•z;
4° x • x ³ 0,причем скалярный квадрат x•x= 0 ↔ х= 0.
В
Евклидовых пространствах можно ввести
понятие длины
вектора
(модуль вектора)
и угол между
векторами
.
Нужно показать, что ïcos jï£ 1.
Для этого докажем неравенство Коши - Буняковского (Шварца):
0£│a • b│£│a│·│b│.
Док-во: Рассмотрим скалярный квадрат
(a- lb)•(a- lb)= a • a- la • b- l a • b + l2b • b= │a│2- 2la • b+ l2│b│2³ 0, как скалярный квадрат.
Последнее неравенство рассмотрим как квадратное относительно l.
l2│b│2- 2λa•b +│a│2³ 0.
Чтобы это неравенство выполнялось при любом λ, нужно, чтобы дискриминант D£ 0.
D= b2- 4ac= (-2a•b)2- 4│b│2·│a│2£ 0.
4(a•b) 2- 4│b│2·│a│2£ 0 ê: 4;
(a•b) 2£ │b│2·│a│2.
Извлекаем
корень
:
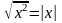0£│a • b│£│a│·│b│.
Ч.т.д.
На основании неравенства Коши - Буняковского определение косинуса угла между векторами Евклидова пространства корректно.
Замечание: Евклидово пространства размерности n принято обозначать En,
E2 - евклидово пространство всех векторов на плоскости, E3 - в пространстве.
Скалярное произведение векторов в ортонормированном базисе.
Определение: Два вектора Евклидова пространства называются ортогональными, если их скалярное произведение равно нулю.
Определение: Базис Евклидова пространства l1, l2, ... ,ln называется ортонормированным, если векторы l1, l2, ... ,ln попарно ортогональны и длина каждого вектора равна 1, т.е.
.
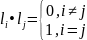Пусть вектора x, y заданы своими координатами в ортонормированном базисе l1, l2, ... ,ln:
х =(α1, α2,… αn)= α1 l1+ α2 l2+ ... +αn ln, у = (β1, β2, … βn)= β1 l1+ β2l2+…+βn ln.
Найдем их скалярное произведение:
x•y=(α1, α2,… αn)•(β1, β2, … βn)= (α1 l1+ α2 l2+ ... +αn ln)•( β1 l1+ β2l2+…+βn ln)=
= α1 l1 •β1 l1+ α1 l1 •β2l2+…+ α1 l1 •βn ln+ α2 l2 •β1 l1+ α2 l2 •β2l2+…+
+α2 l2 •βn ln+…+ αn ln •β1 l1+ αn ln •β2l2+…+ αn ln •βn ln=
= α1 β1 ( l1 • l1)+ α1 β2(l1 •l2)+…+ α1 βn ( l1 •ln)+ α2 β1(l2 •l1)+ α2 β2(l2 •l2)+…+
+ α2 βn ( l2 •ln)+…+ αn β1(ln •l1)+ αn β2( ln •l2)+…+ αn βn(ln •ln)=
=(учтем, что вектора l1, l2, ... ,ln – ортонормированный базис)=
= α1 β1+ α2 β2+…+ αn βn.
Т.о. скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат.
Декартовая система координат.
Рассмотрим три ненулевых, не коллинеарных вектора в пространстве l1, l2, l3- это базис ЛП V3. Приведем эти векторы к общему началу в точке О и расположим их по осям.
z
l3
l2
у
O
l1
х
Определение: Совокупность точки и базиса называется декартовой системой координат.
Определение: Если базисные вектора взаимно перпендикулярны, длины их равны 1, то такой базис называется ортонормированным. Базисные вектора называются ортами и обозначаются i, j, k, а система координат называется декартовой прямоугольной системой координат.
Свойство орт:
1) i ┴ j, i ┴ k, j ┴ k;
2) │i│= │j│= │k│= 1.
Декартовых систем координат бесконечное множество.
Определение: Тройка векторов a, b, c называется правой, если кратчайший поворот от вектора a к b, видимый с конца вектора с будет против часовой стрелки.
Если такой поворот по часовой стрелке, то тройка векторов называется левой.
Мы будем рассматривать такие системы координат, в которых базисные вектора образуют только правую тройку.