Библиографический список
Пискунов, Н.С. Дифференциальное и интегральное исчисления : учебник для втузов в 2 т. – М. : Интеграл-Пресс, 2001.
Данко, П.Е. Высшая математика в упражнениях и задачах. В 2-х частях.: Учеб. пособие для втузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М. : Высш. шк., 1999.
Задания для контрольной работы
Вариант 1
Исследовать сходимость рядов 1)
,
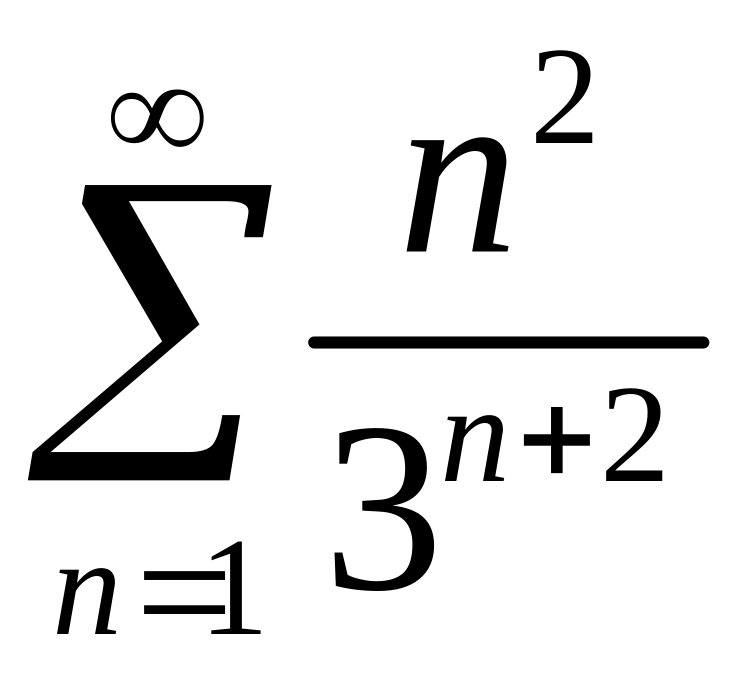2)
.
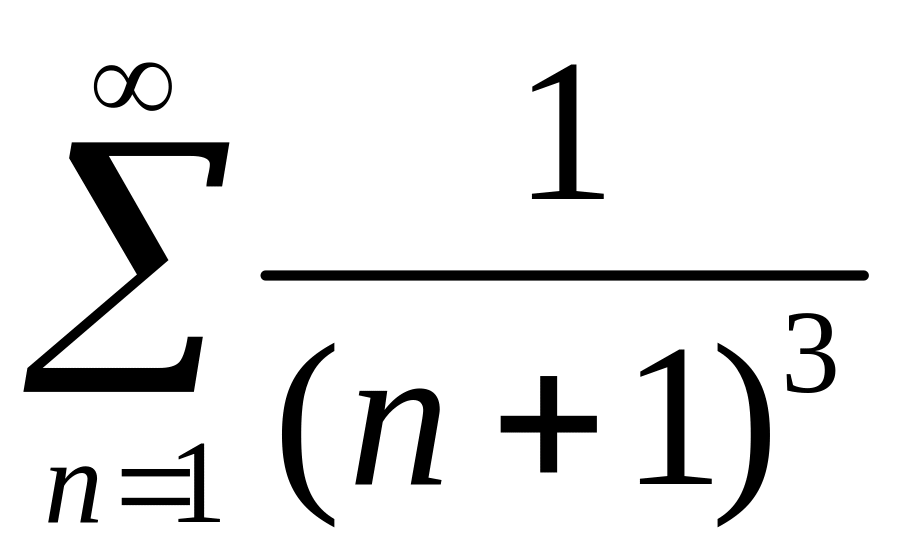Исследовать сходимость знакопеременных рядов
1)
,
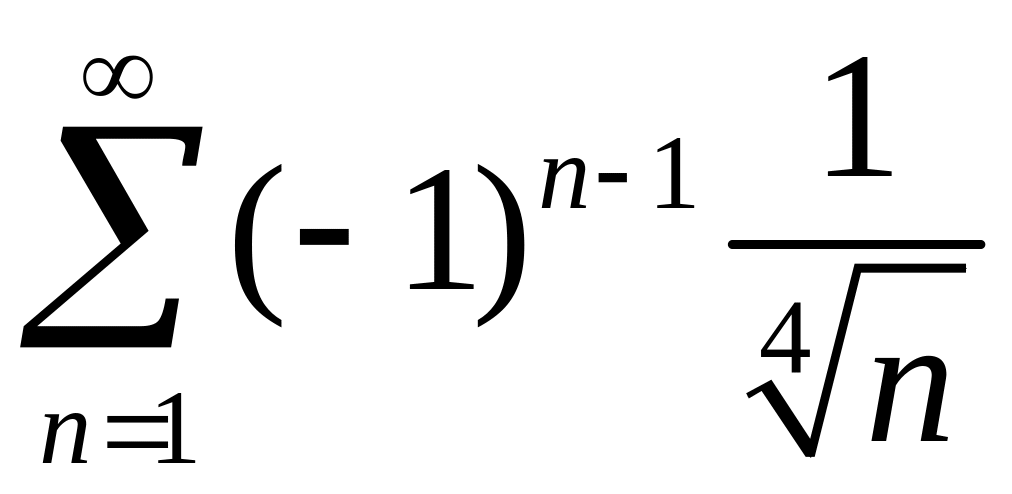2)
.
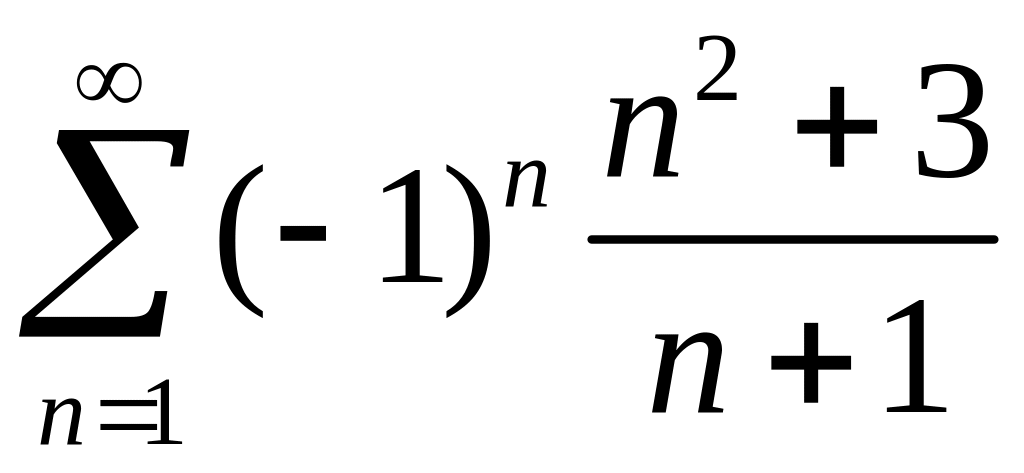Найти область сходимости степенного ряда
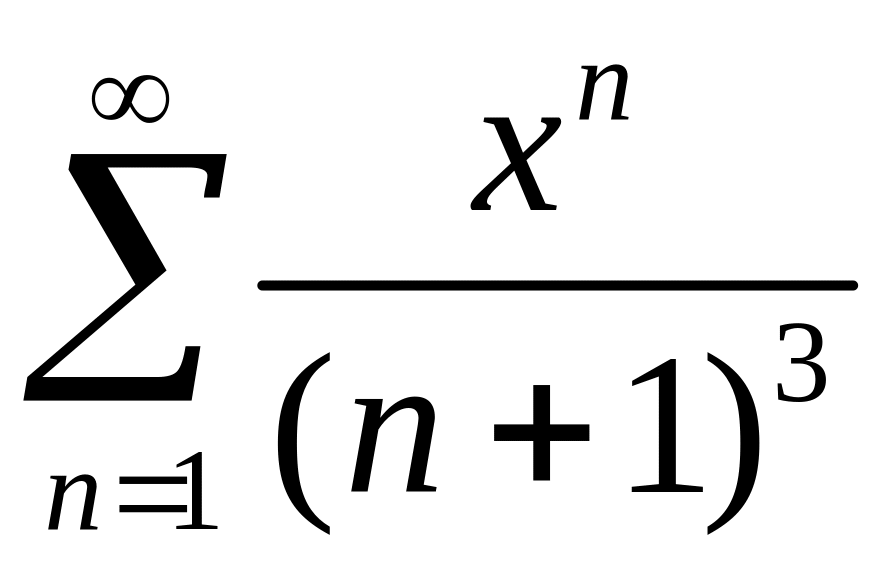.Функцию
разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
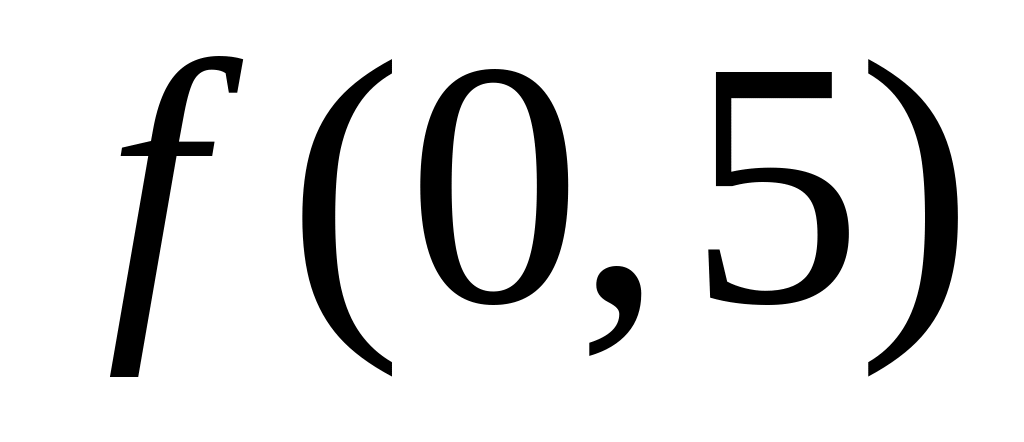с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
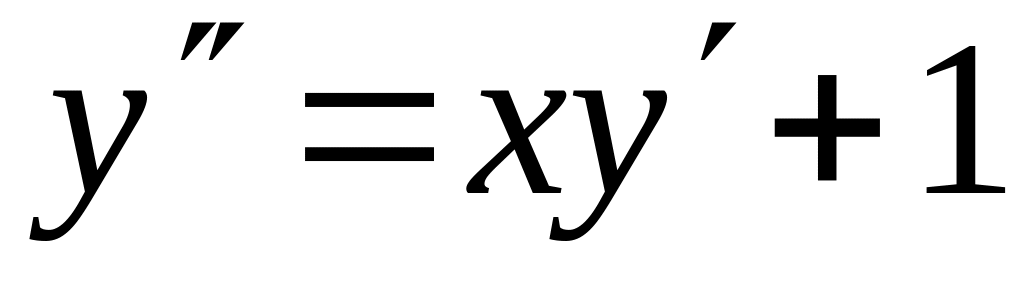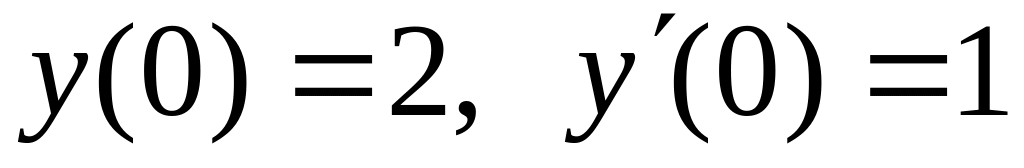.Разложить в ряд Фурье
.
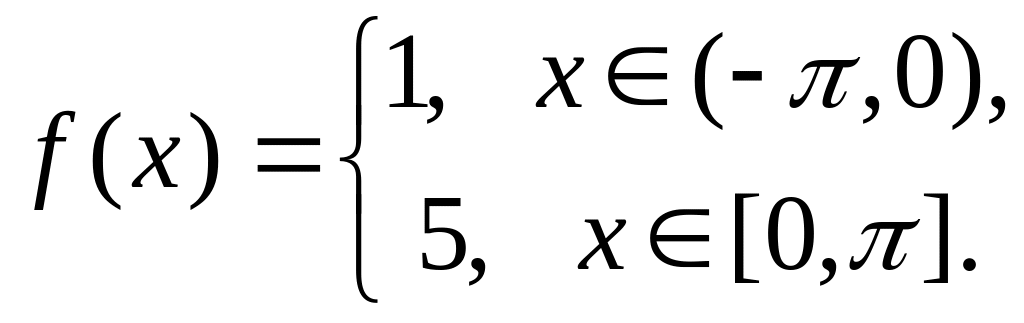
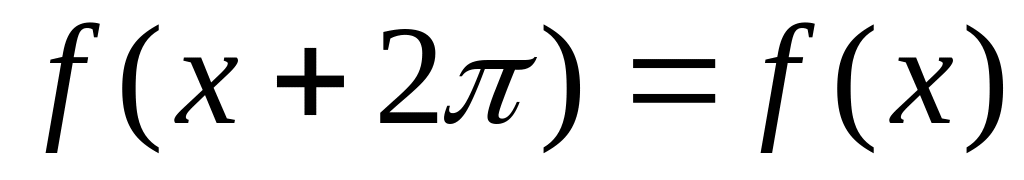Вариант 2
Исследовать сходимость рядов 1)
,
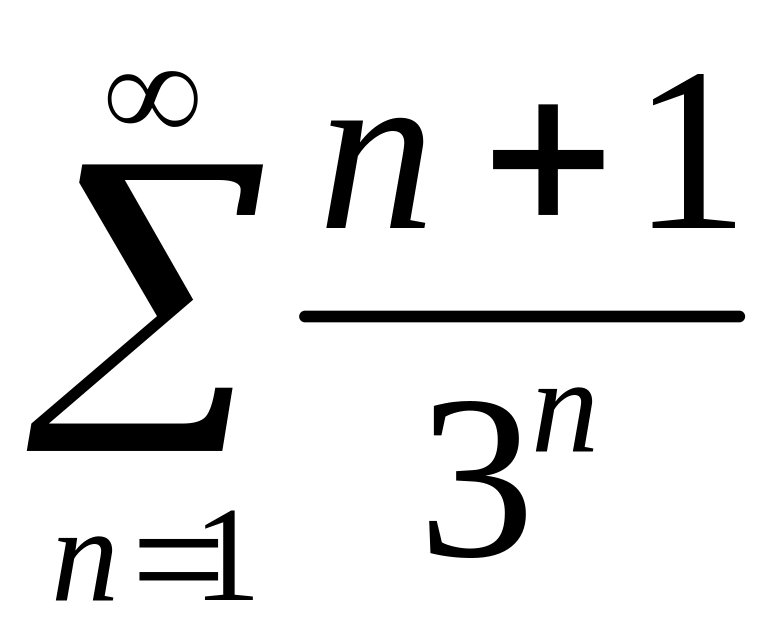2)
.
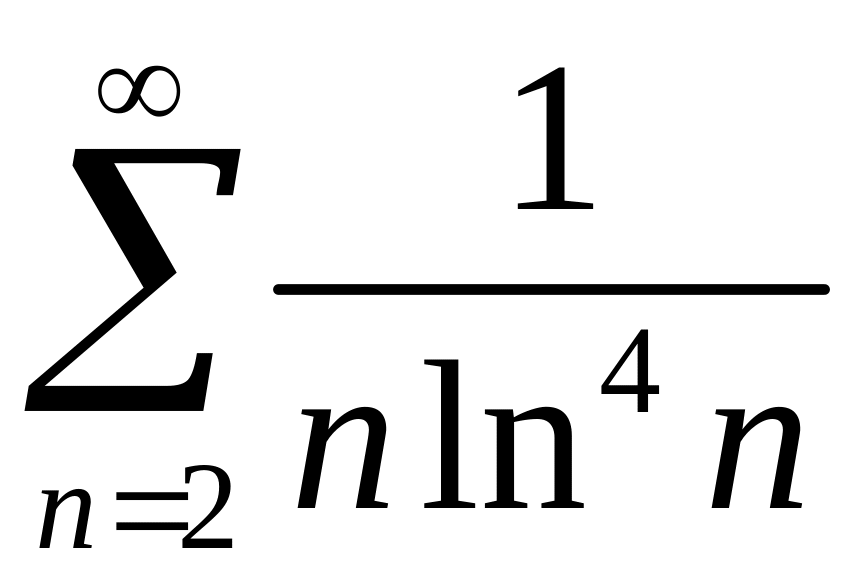Исследовать сходимость знакопеременных рядов
1)
,
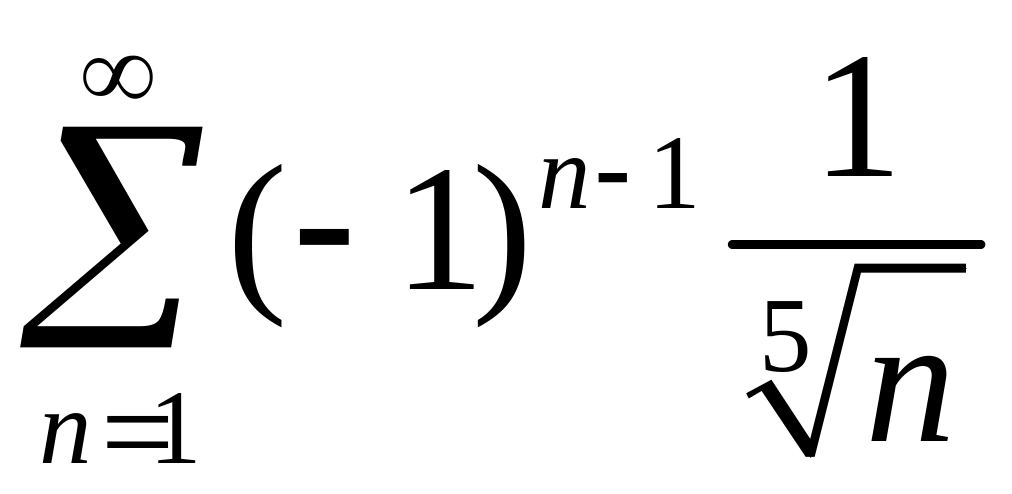2)
.
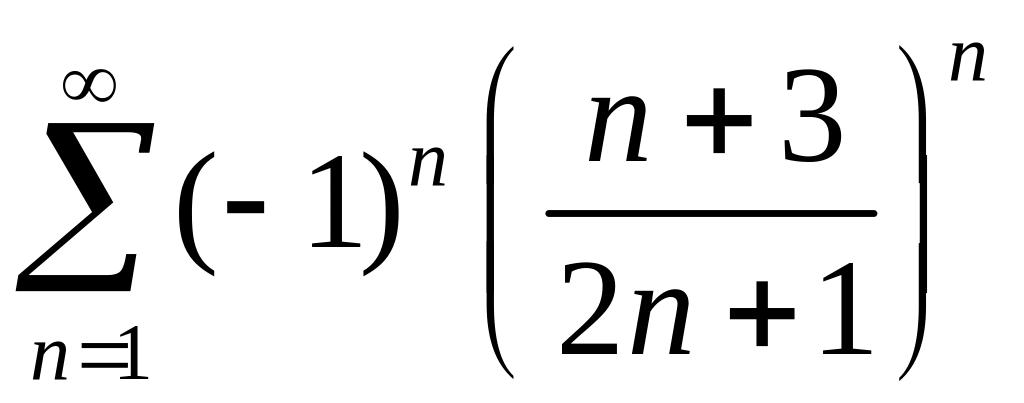Найти область сходимости степенного ряда
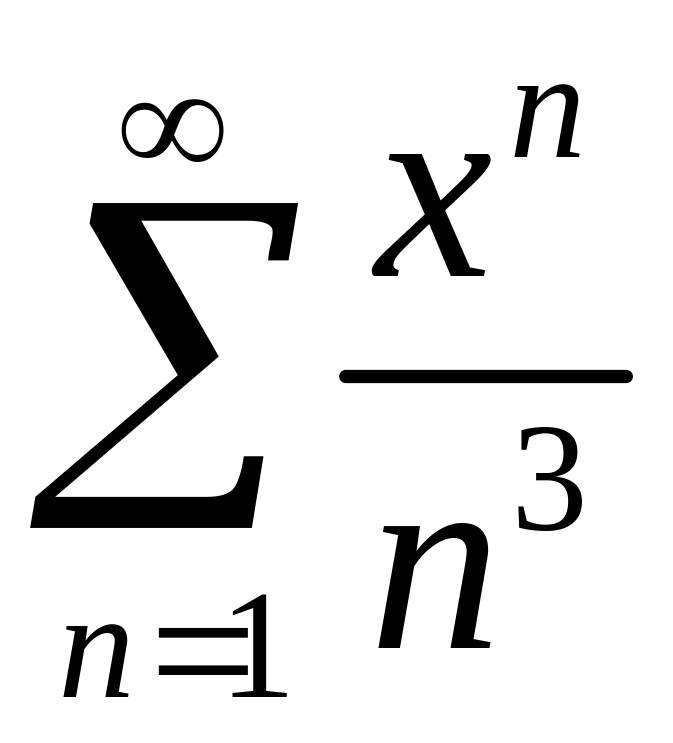.Функцию
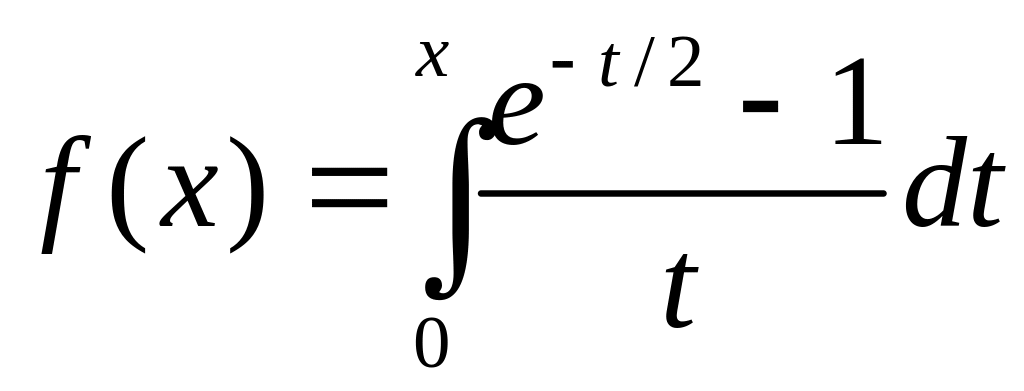разложить в ряд по степеням
.
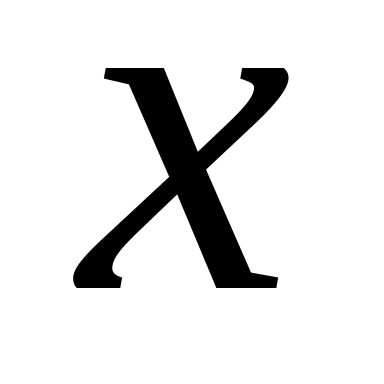Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням
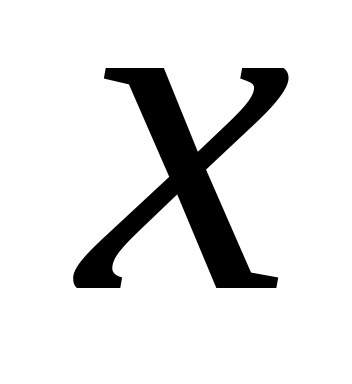решения
дифференциального уравнения
,
.
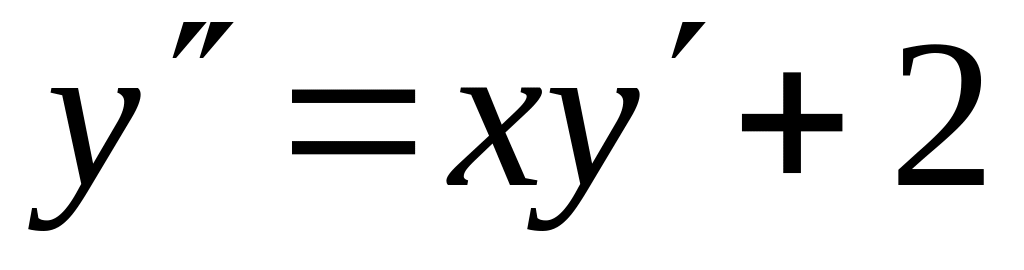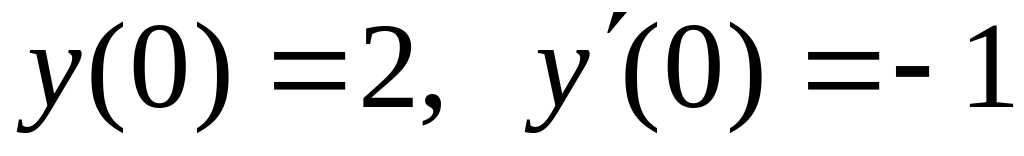Разложить в ряд Фурье
.
Вариант 3
Исследовать сходимость рядов 1)
,
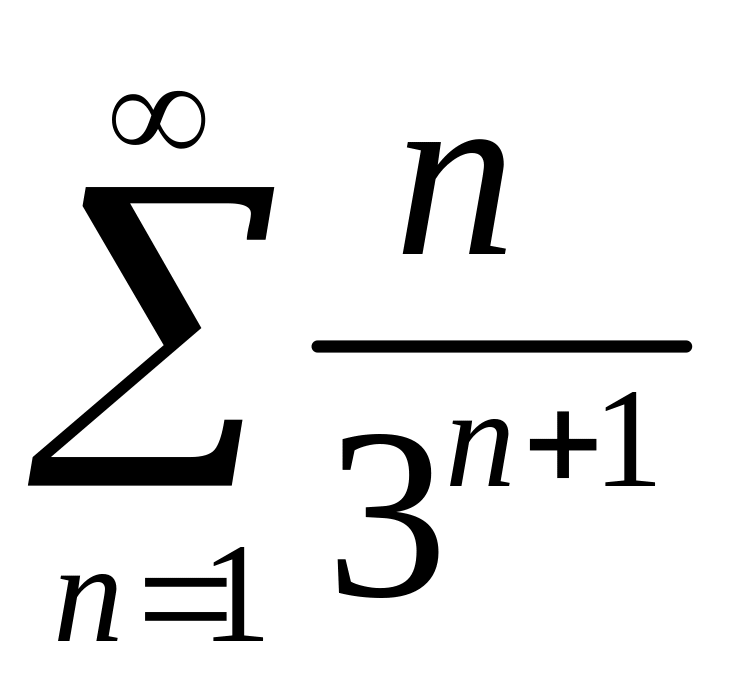2)
.
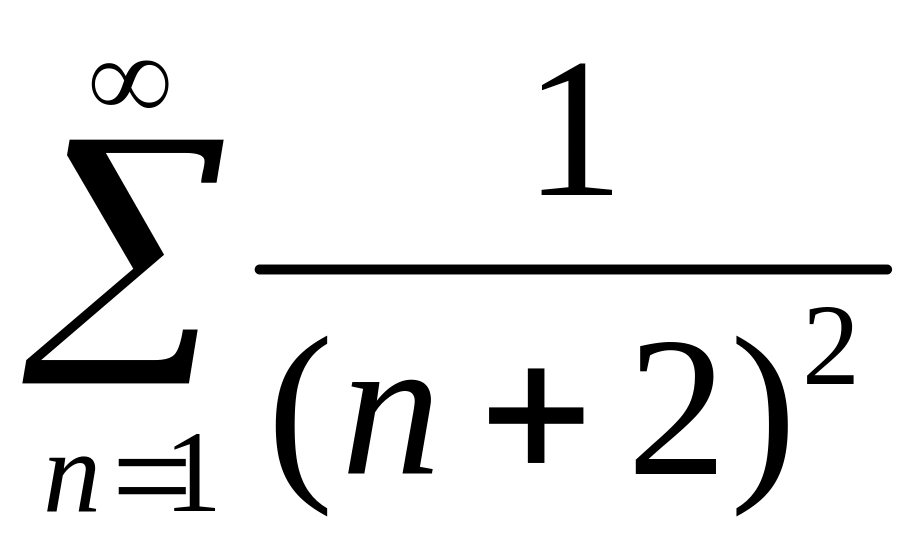Исследовать сходимость знакопеременных рядов
1)
,
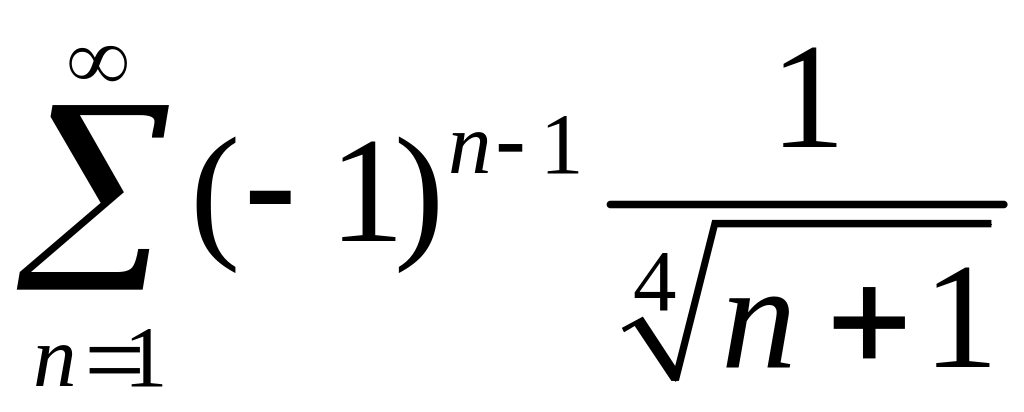2)
.
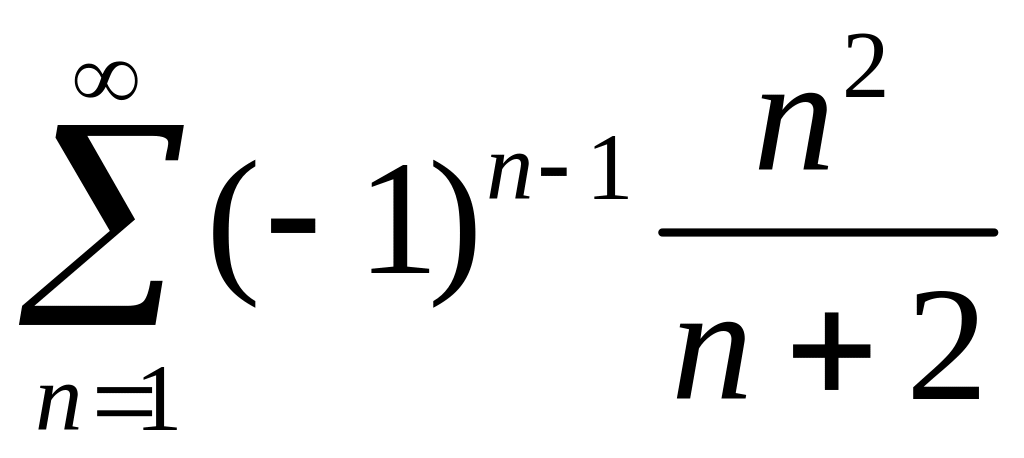Найти область сходимости степенного ряда .
Функцию
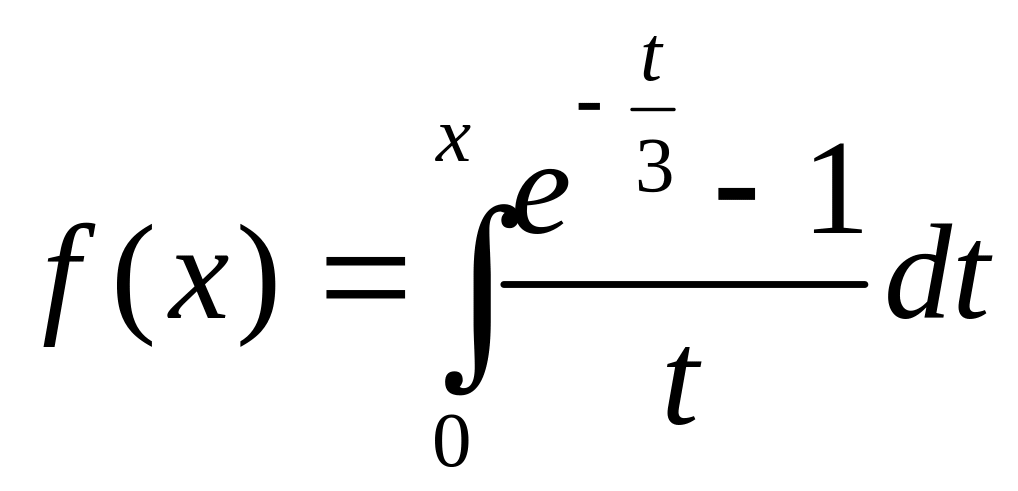разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
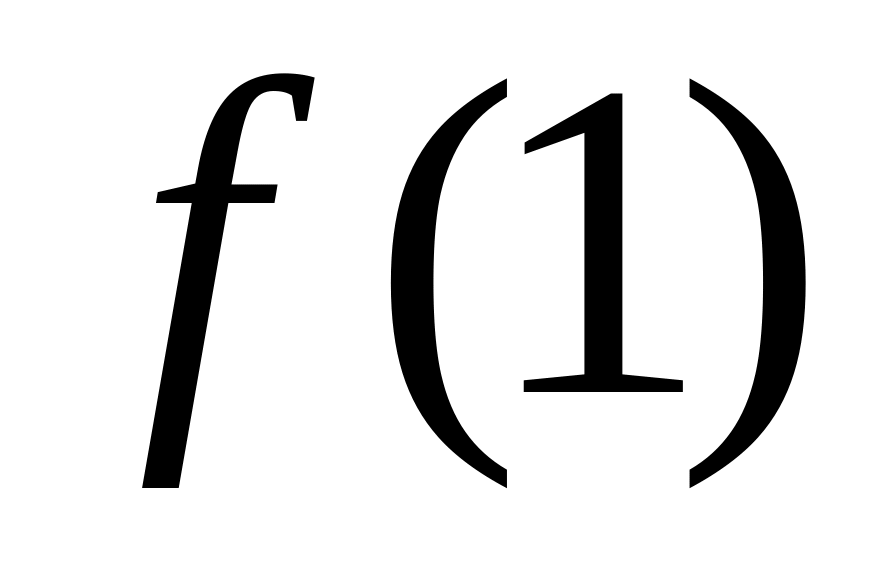с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения ,
.
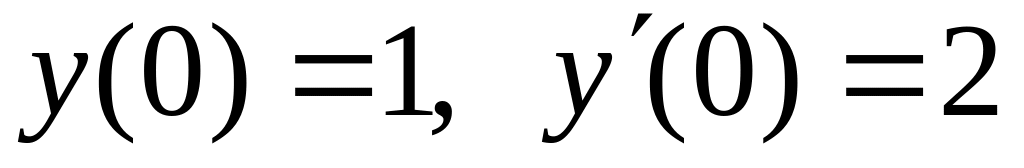Разложить в ряд Фурье
.
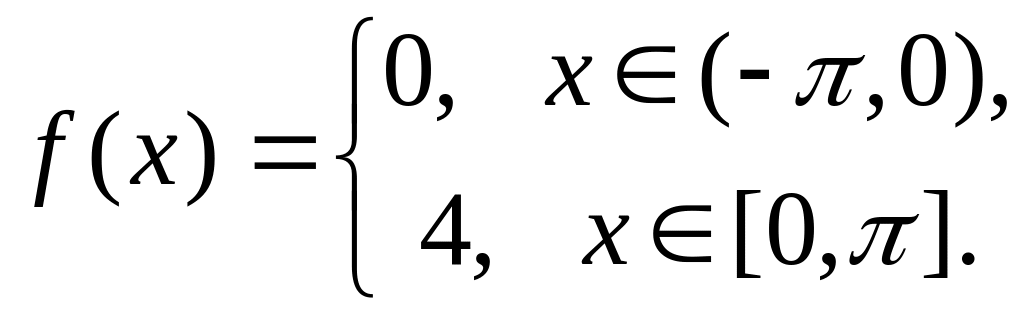Вариант 4
Исследовать сходимость рядов 1)
,
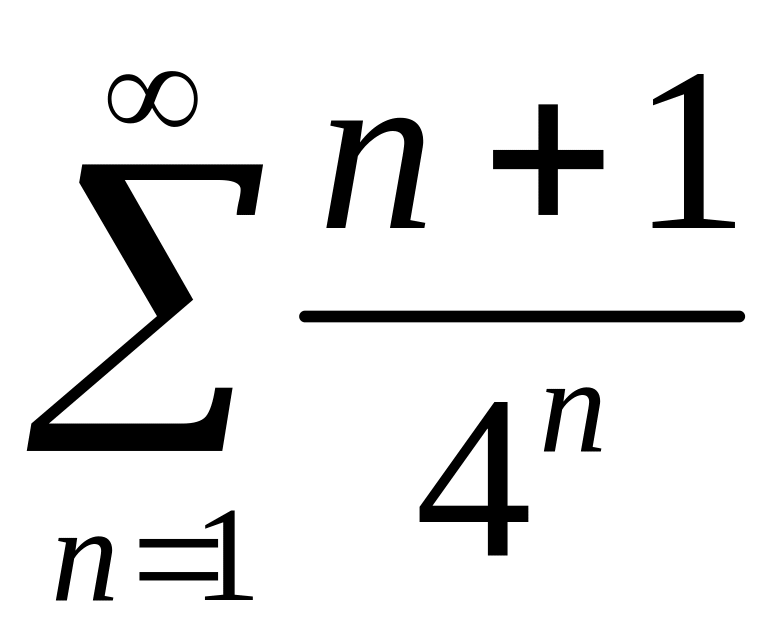2)
.
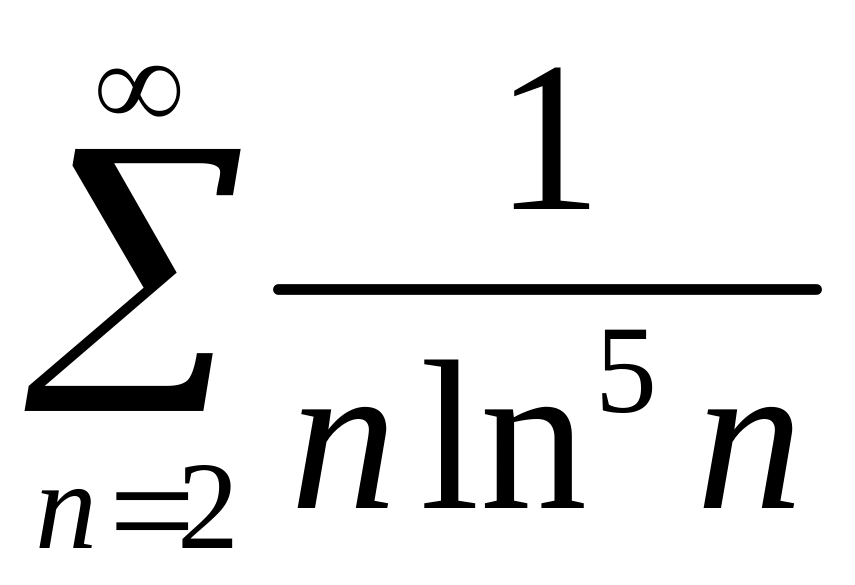Исследовать сходимость знакопеременных рядов
1)
,
2)
.
Найти область сходимости степенного ряда
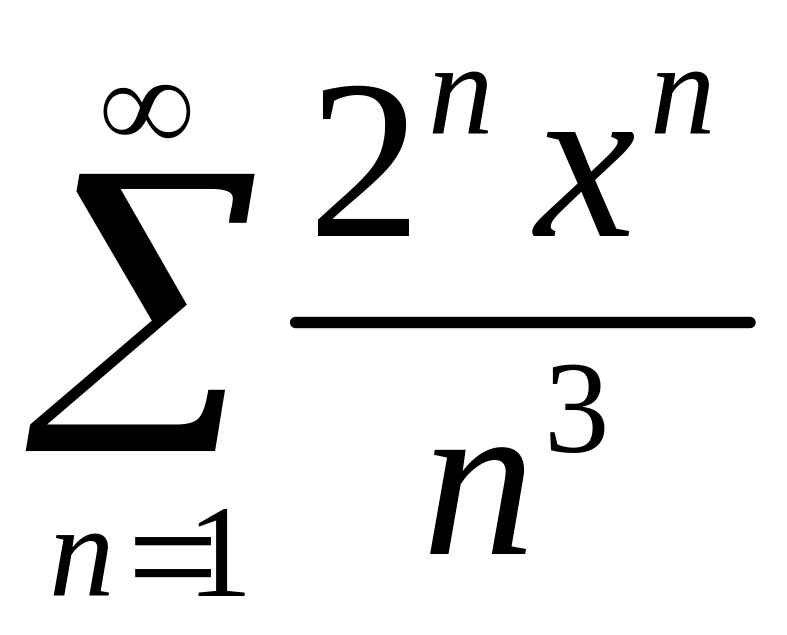.Функцию
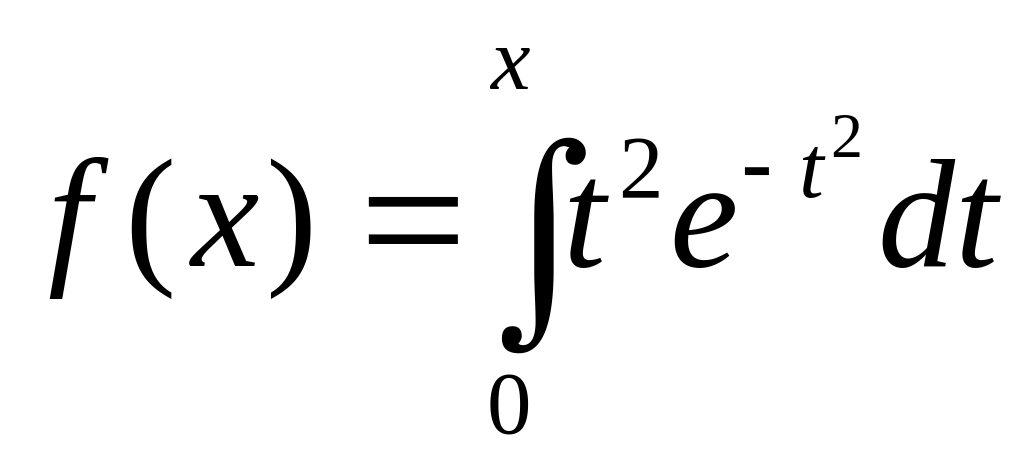разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
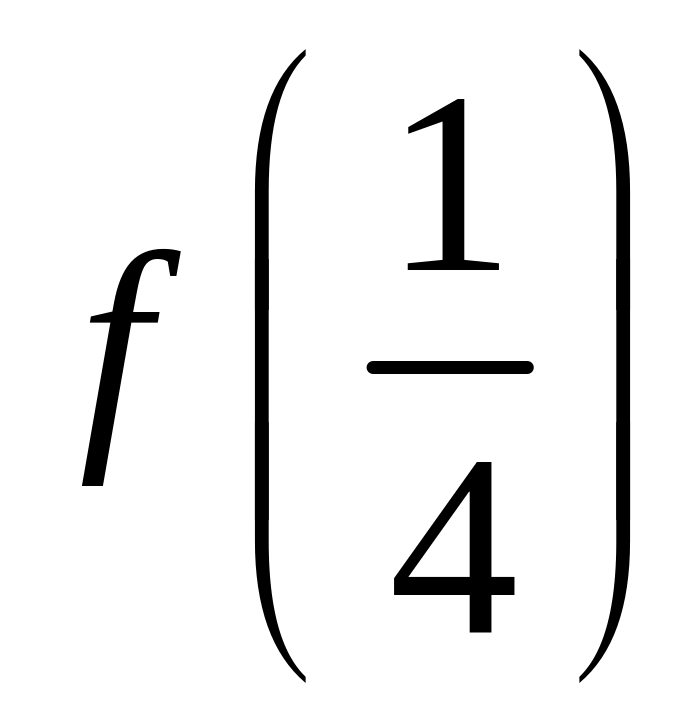с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
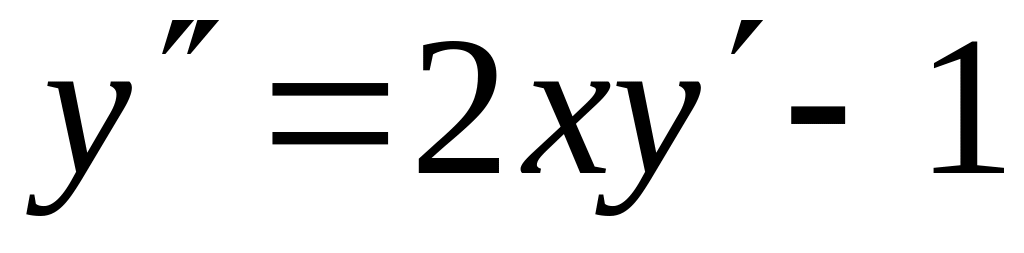.Разложить в ряд Фурье
.
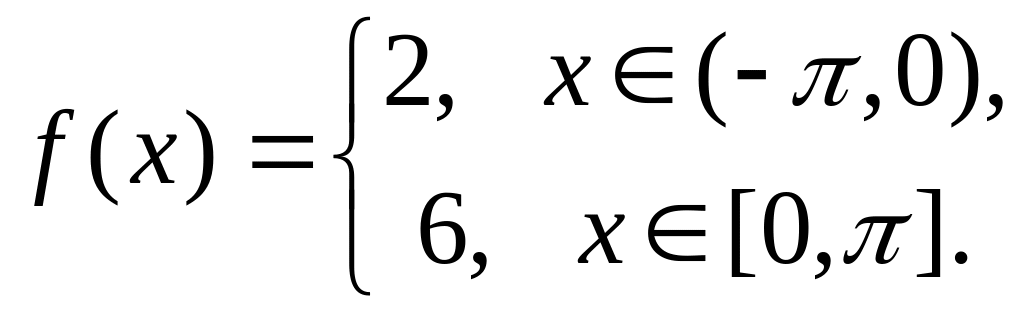Вариант 5
Исследовать сходимость рядов 1)
,
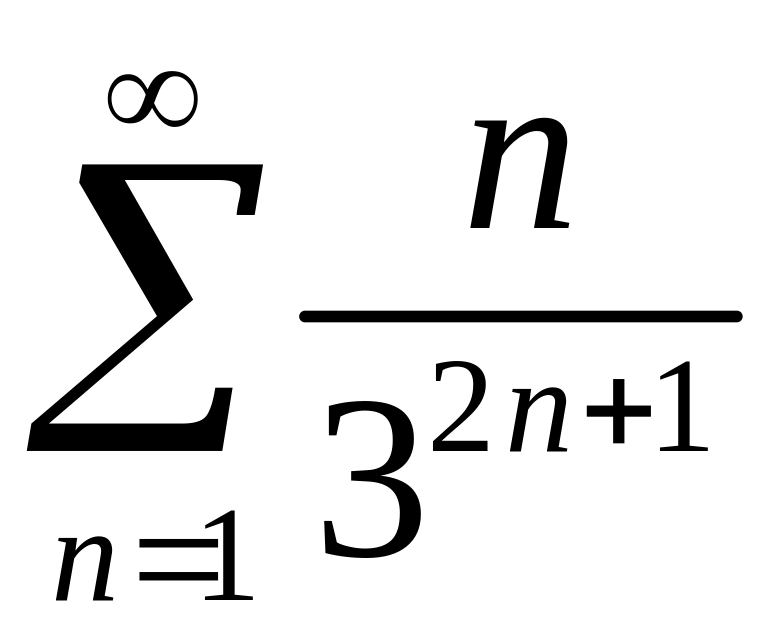2)
.
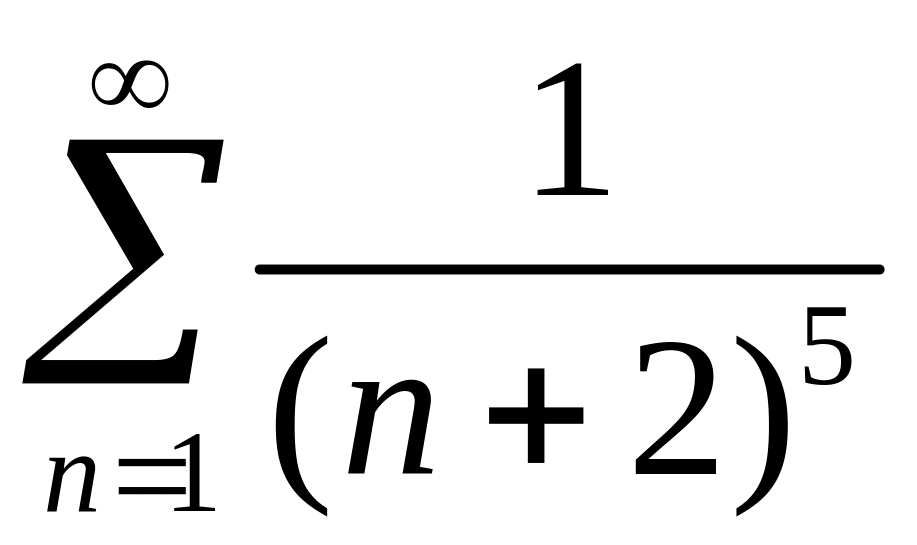Исследовать сходимость знакопеременных рядов
1)
,
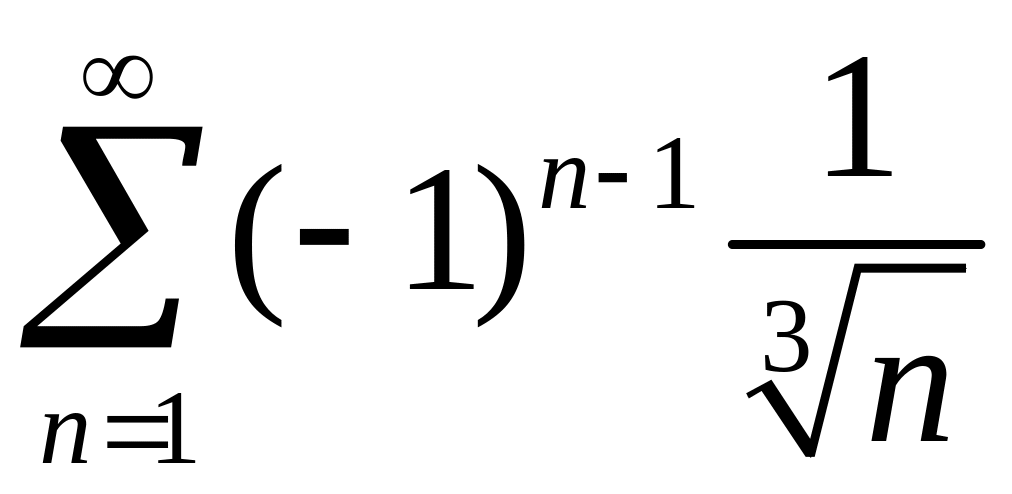2)
.
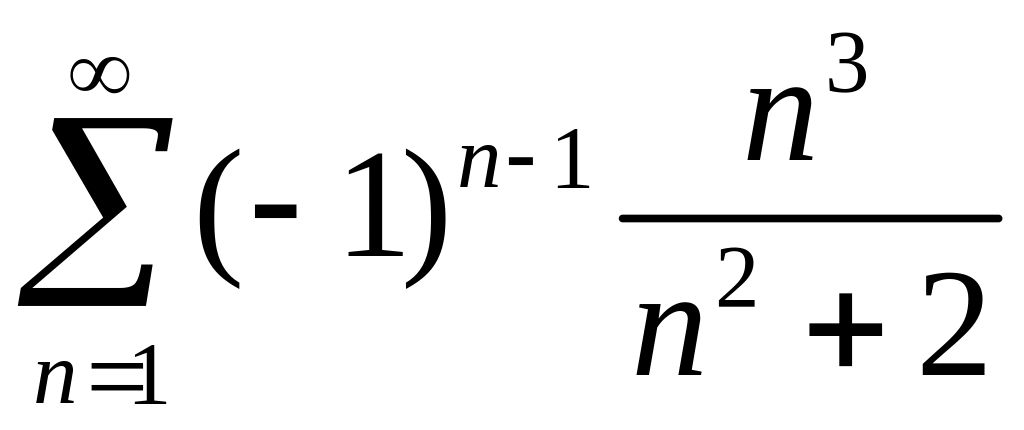Найти область сходимости степенного ряда
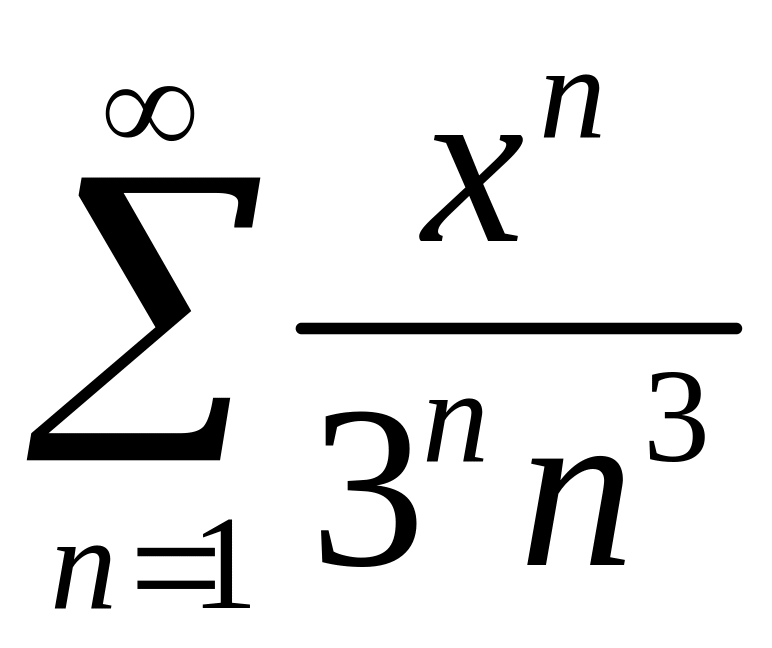.Функцию
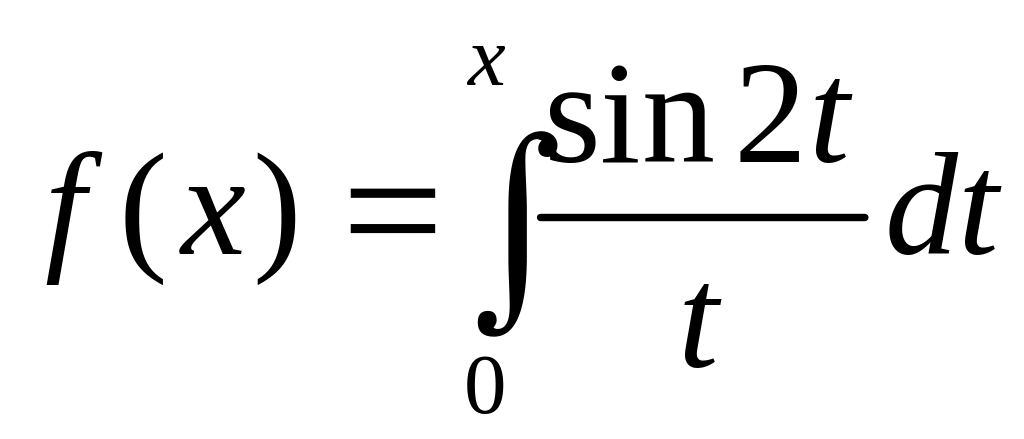разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
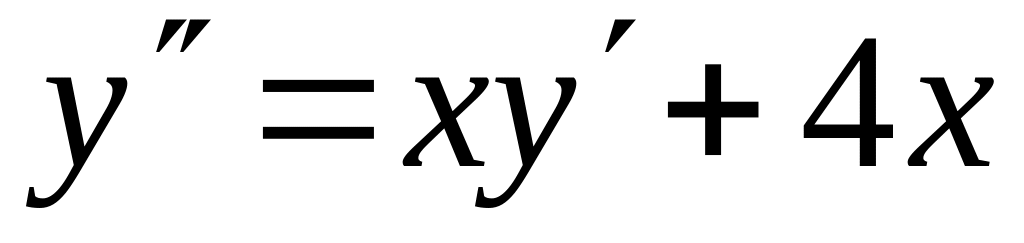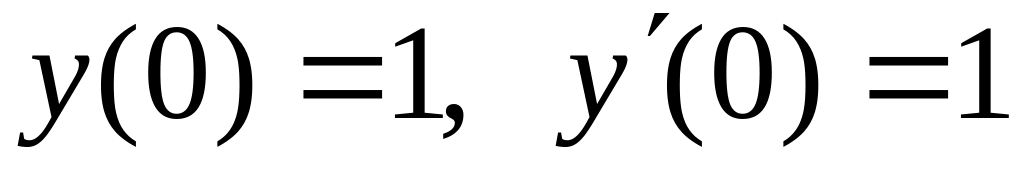.Разложить в ряд Фурье
.
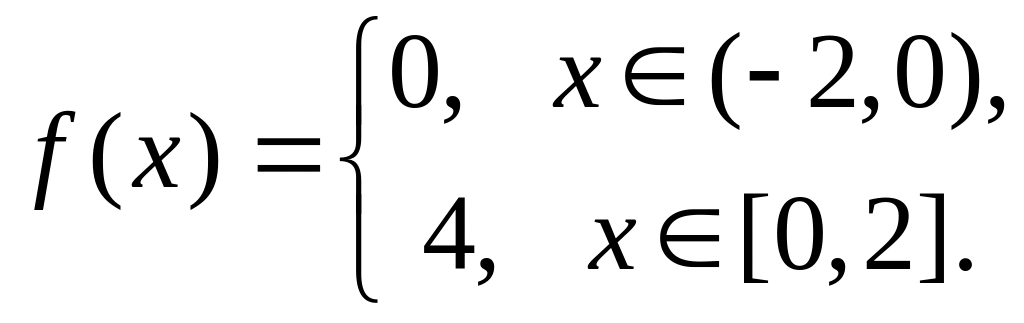
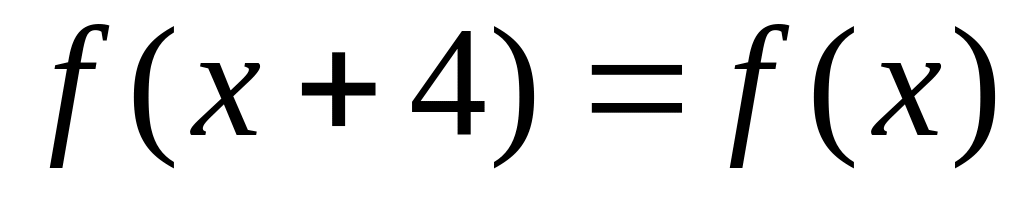Вариант 6
Исследовать сходимость рядов 1)
,
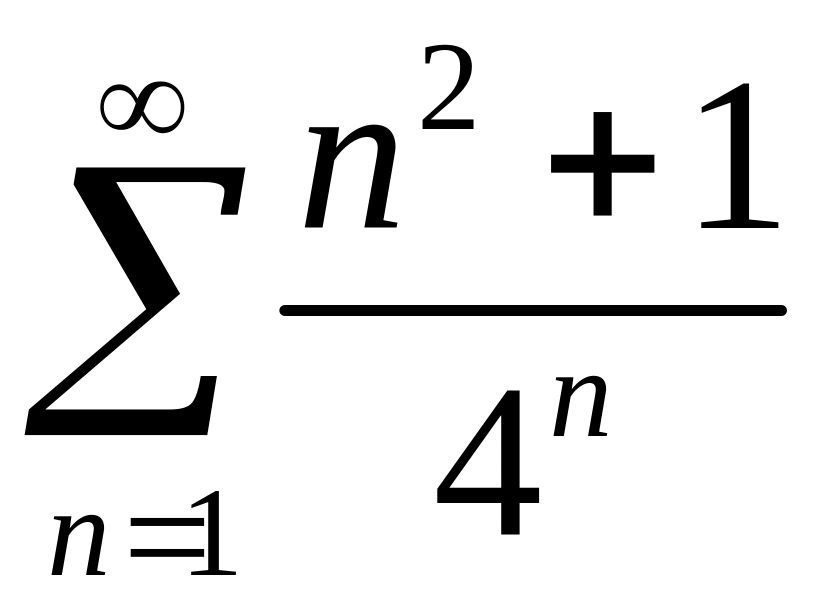2)
.
Исследовать сходимость знакопеременных рядов
1)
,
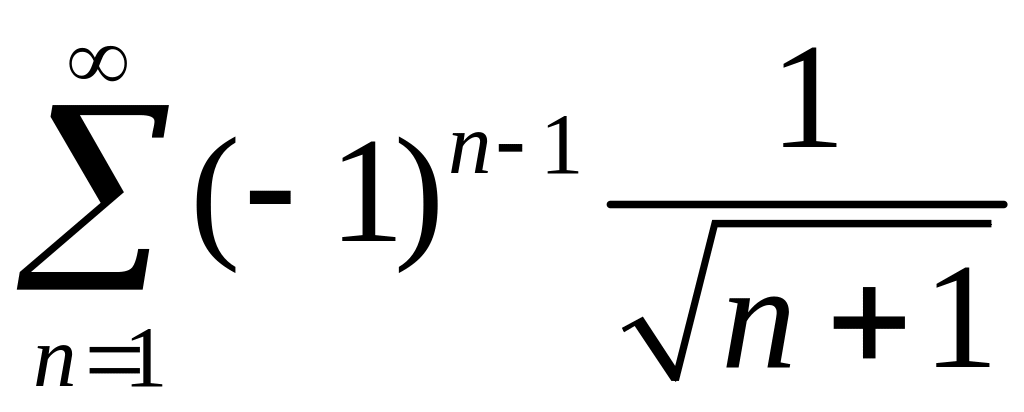2)
.
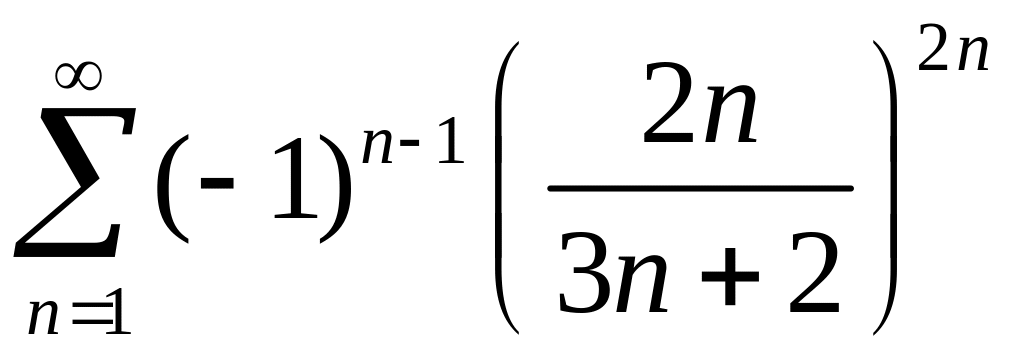Найти область сходимости степенного ряда
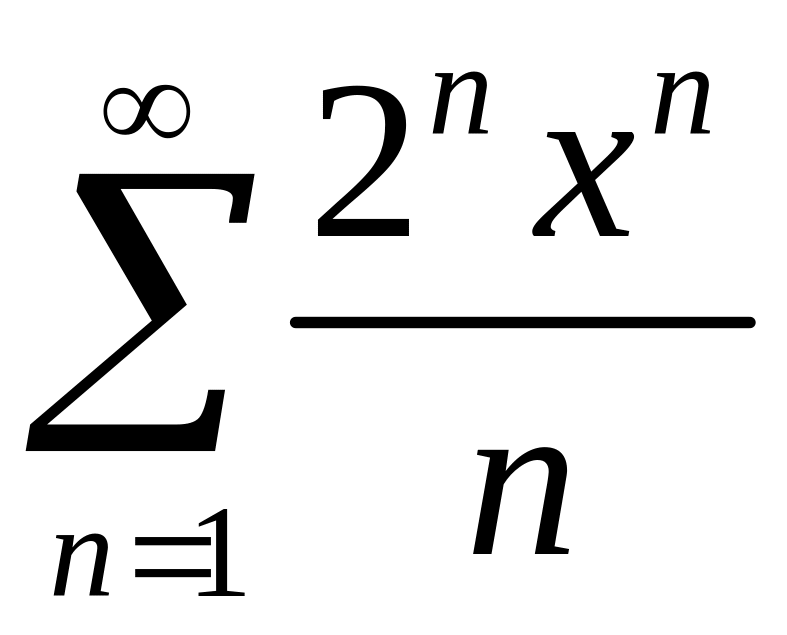.Функцию
разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
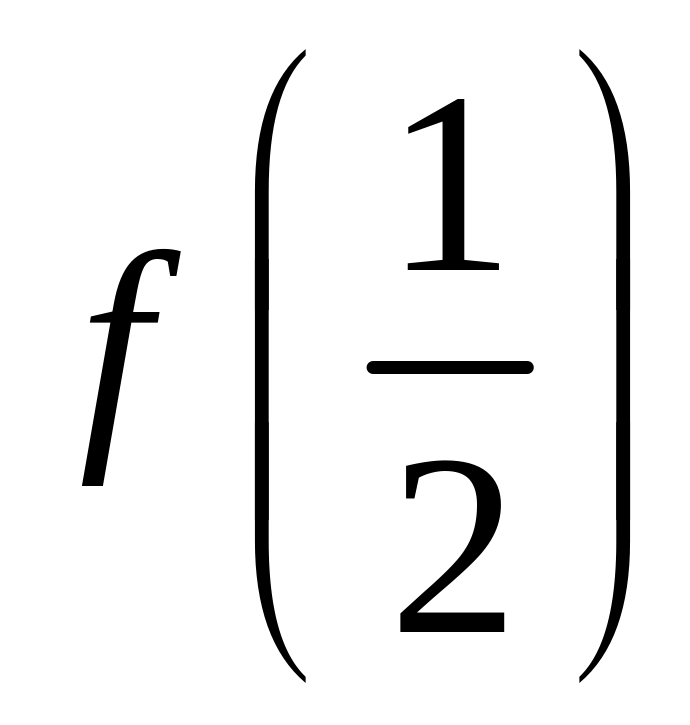с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
.Разложить в ряд Фурье
.
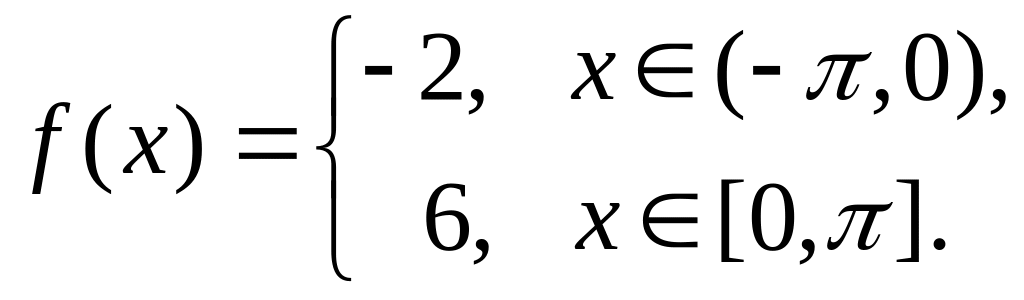Вариант 7
Исследовать сходимость рядов 1)
,
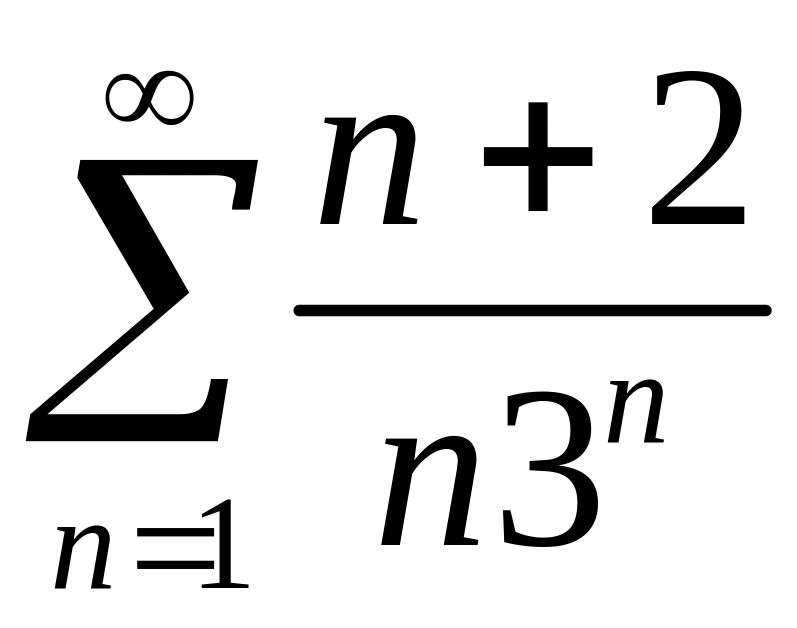2)
.
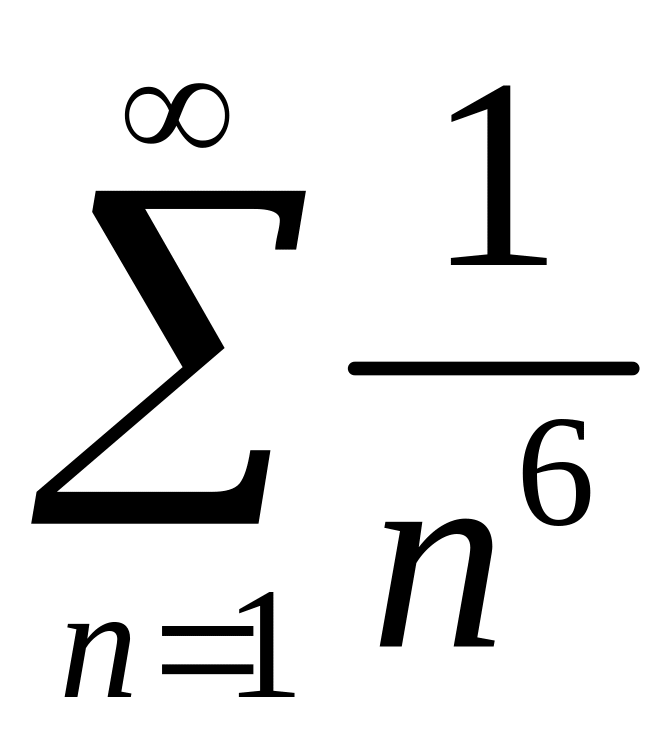Исследовать сходимость знакопеременных рядов
1)
,
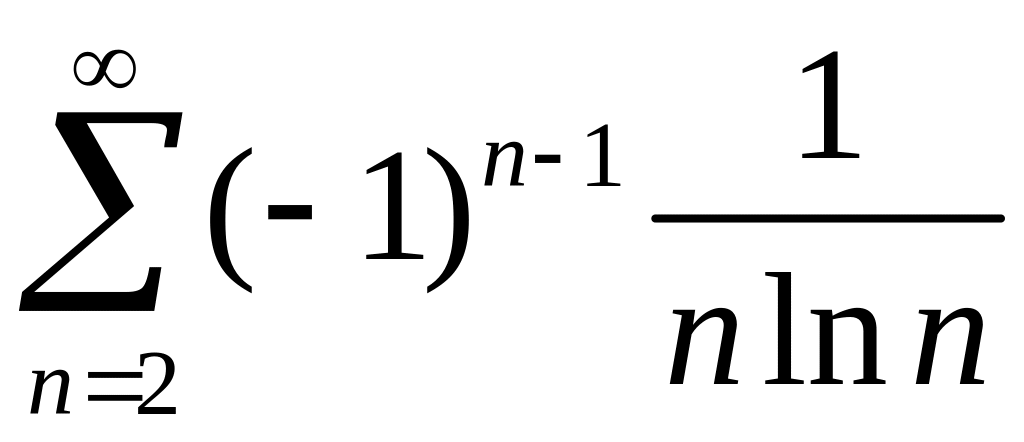2)
.
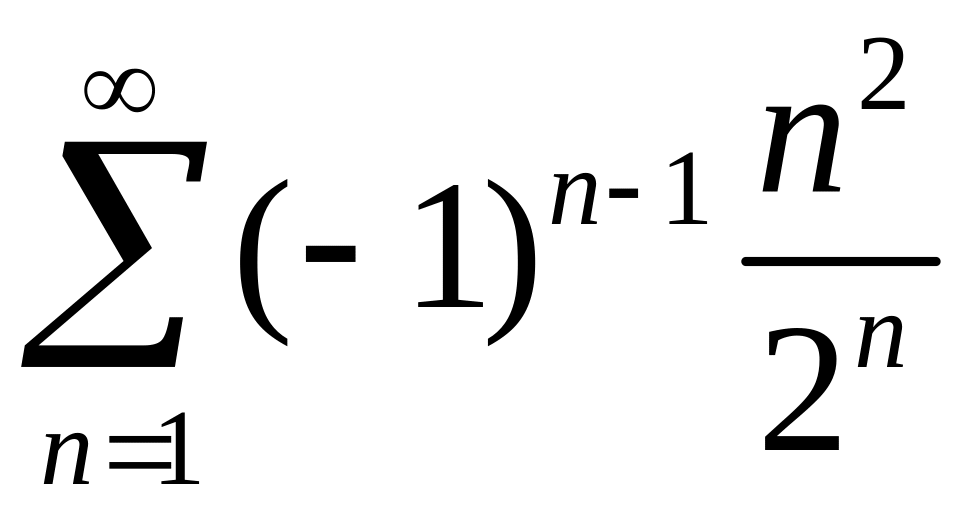Найти область сходимости степенного ряда
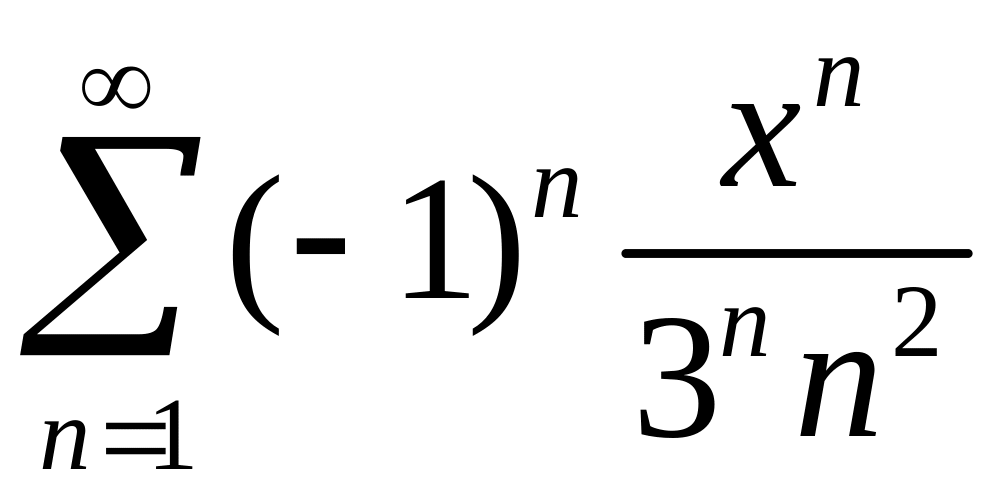.Функцию
разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
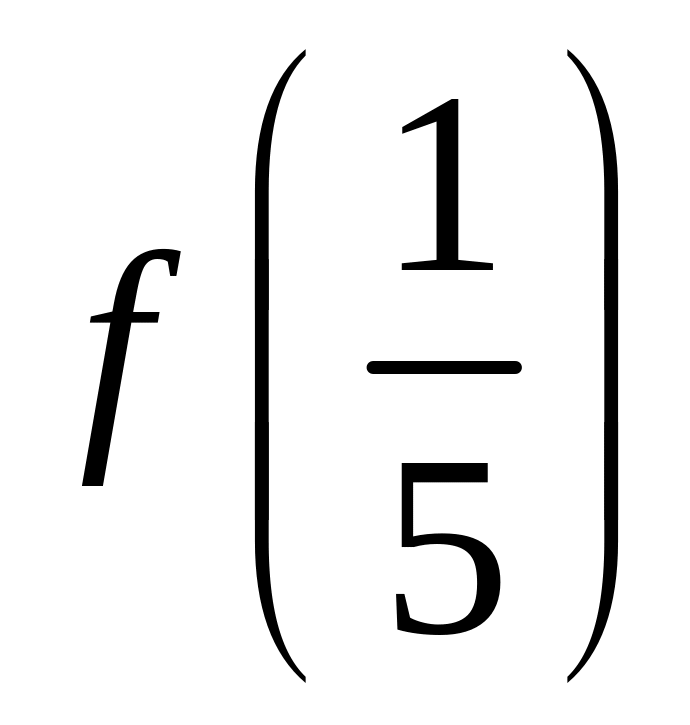с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
.Разложить в ряд Фурье
.
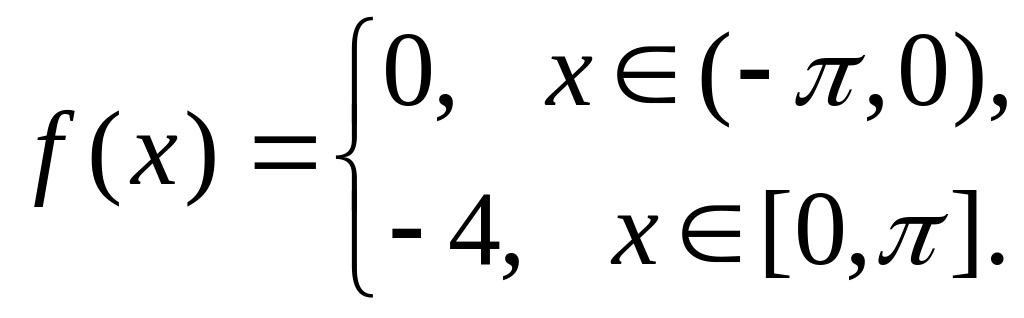Вариант 8
Исследовать сходимость рядов 1)
,
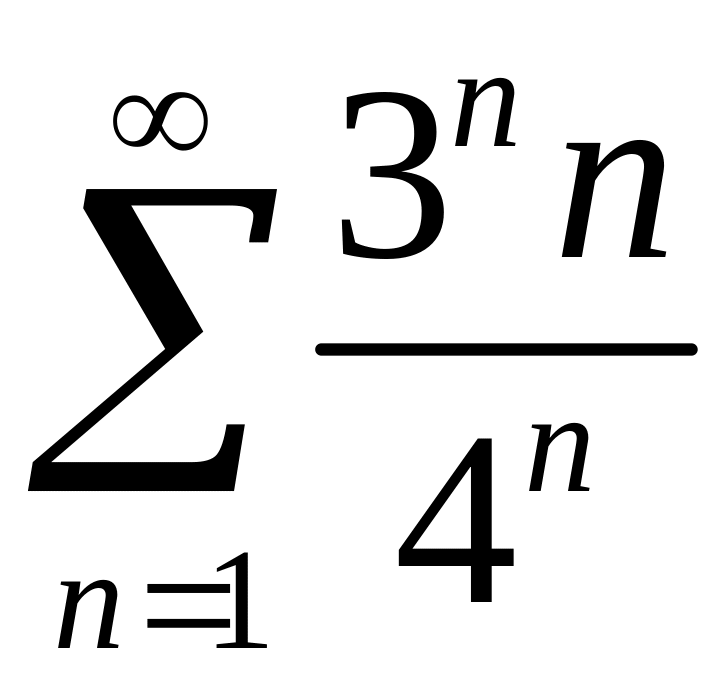2)
.
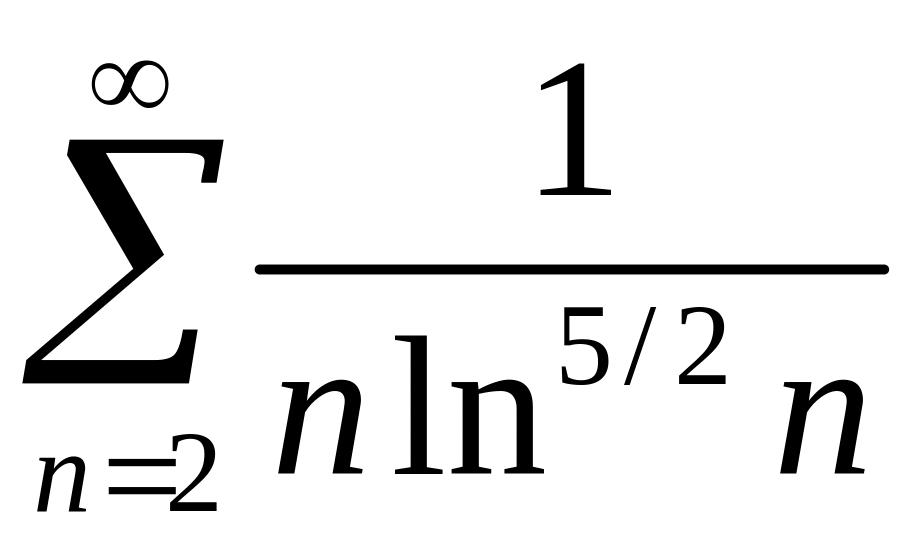Исследовать сходимость знакопеременных рядов
1)
,
2)
.
Найти область сходимости степенного ряда
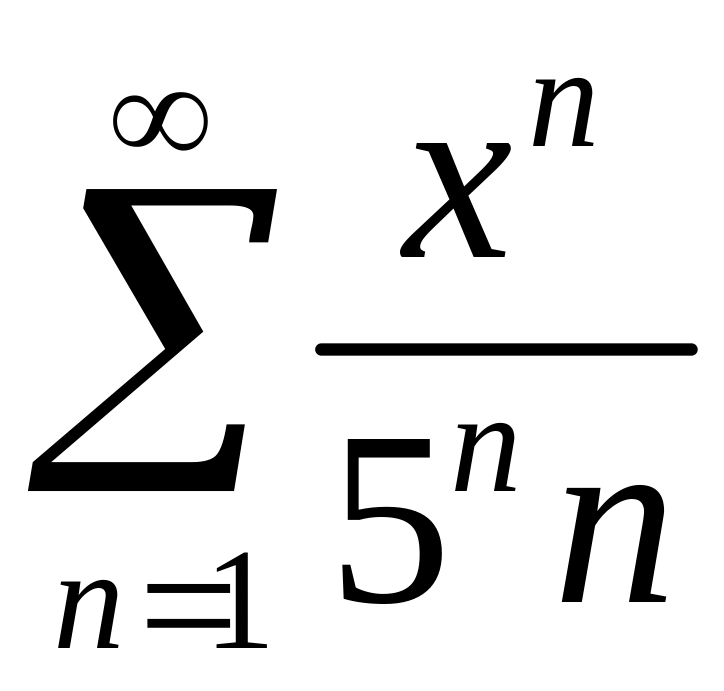.Функцию
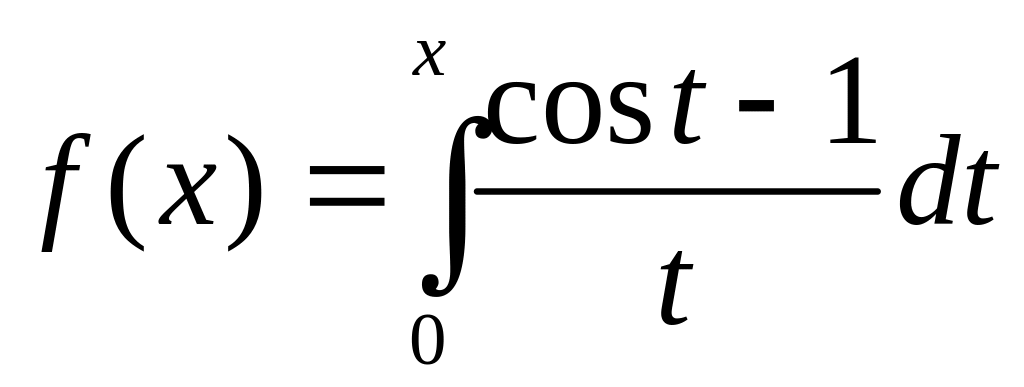разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
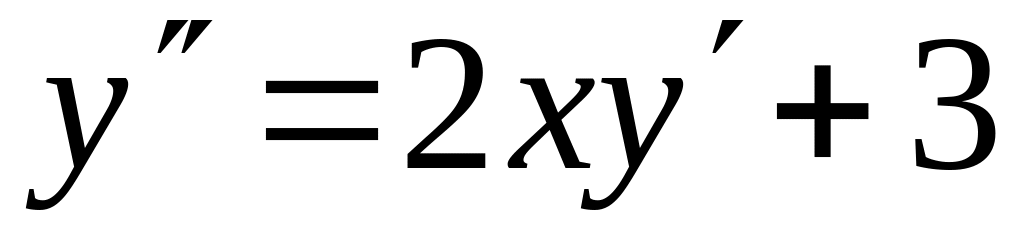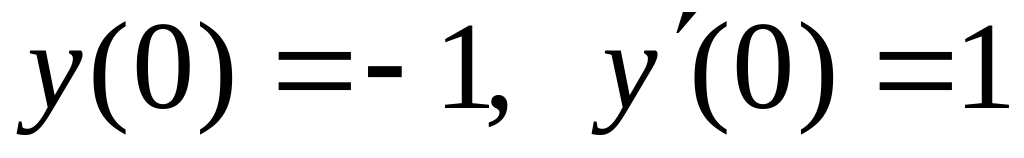.Разложить в ряд Фурье
.
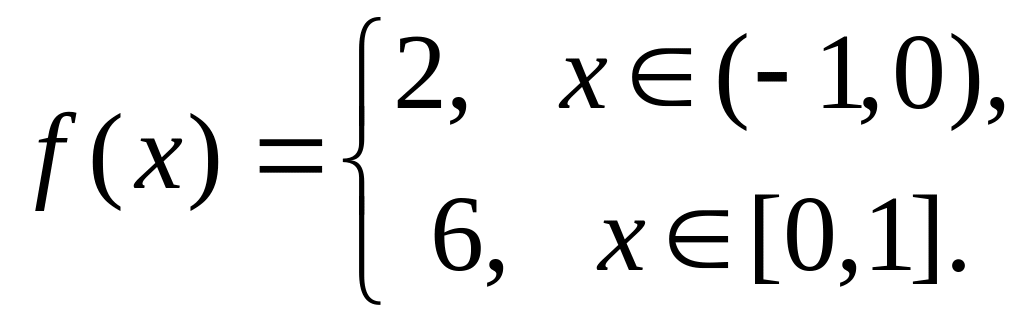
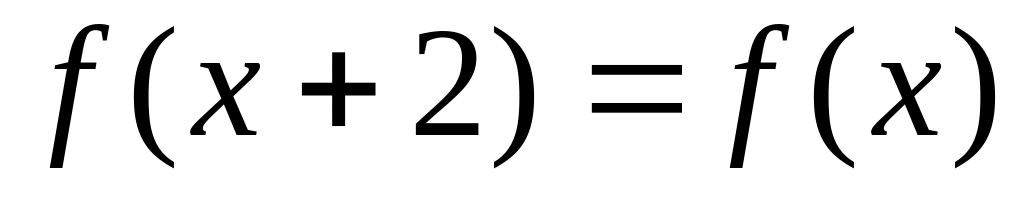Вариант 9
Исследовать сходимость рядов 1)
,
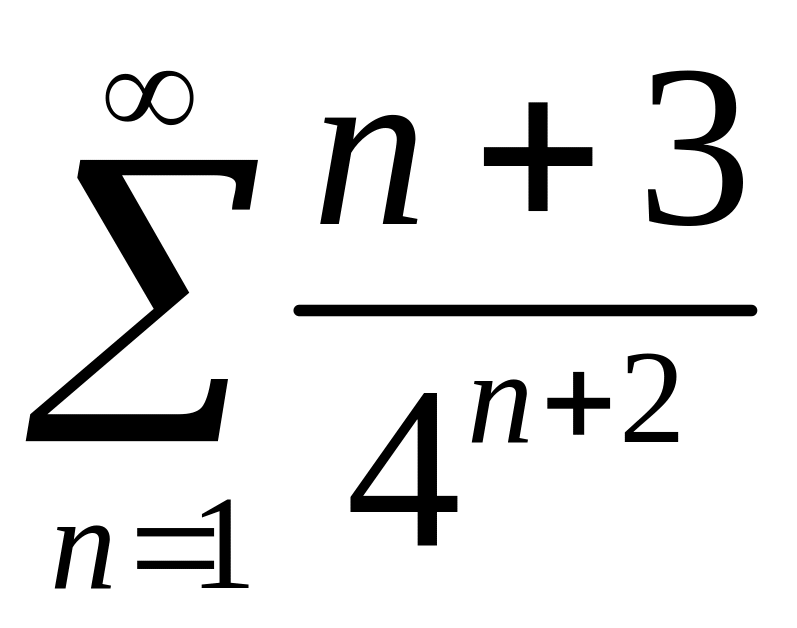2)
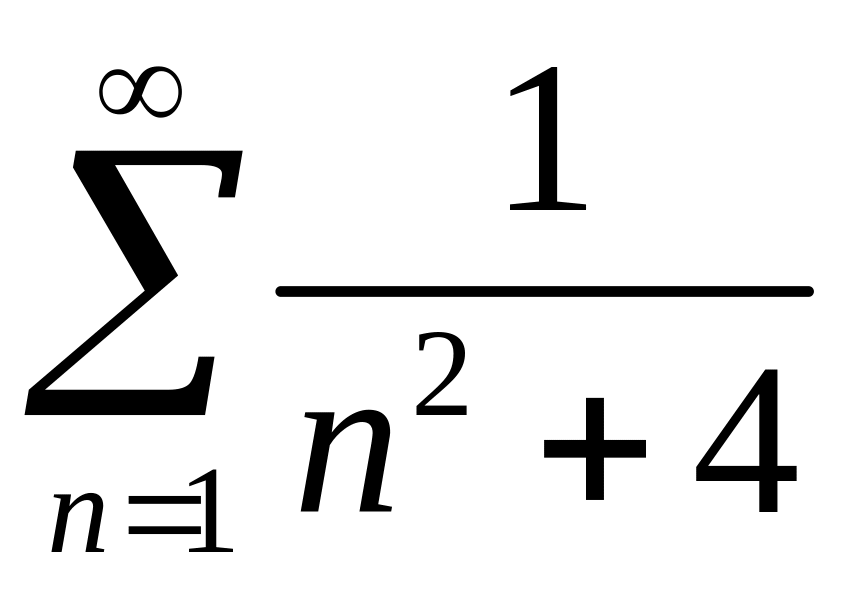.Исследовать сходимость знакопеременных рядов
1)
,
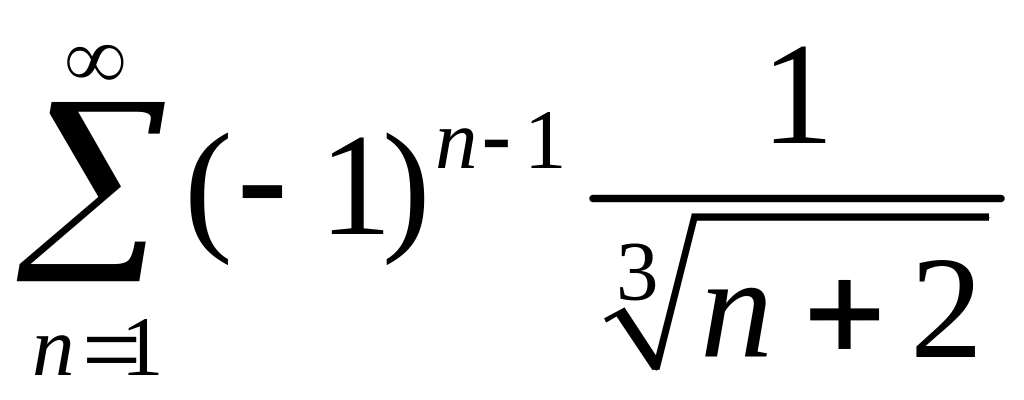2)
.
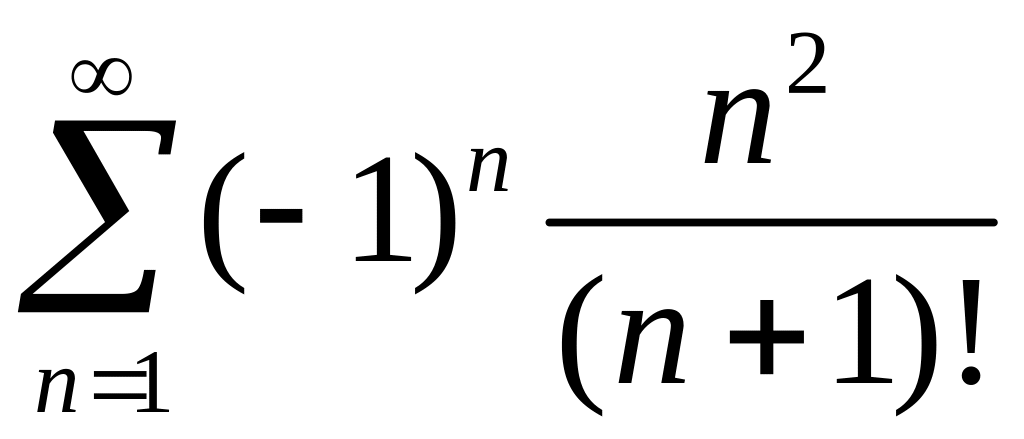Найти область сходимости степенного ряда .
Функцию
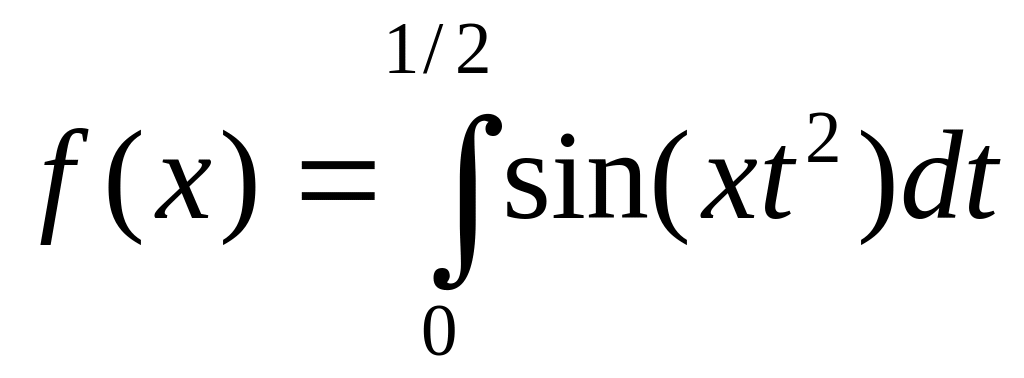разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
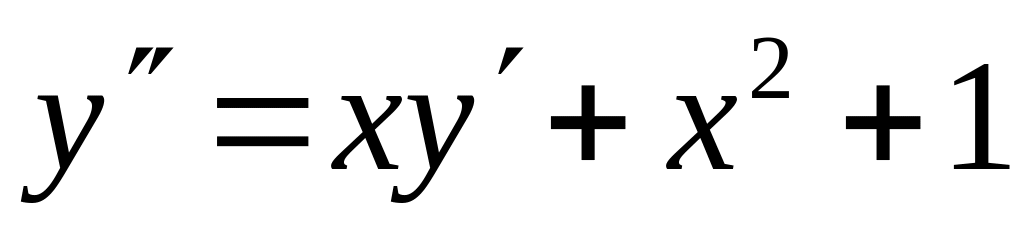.Разложить в ряд Фурье
.
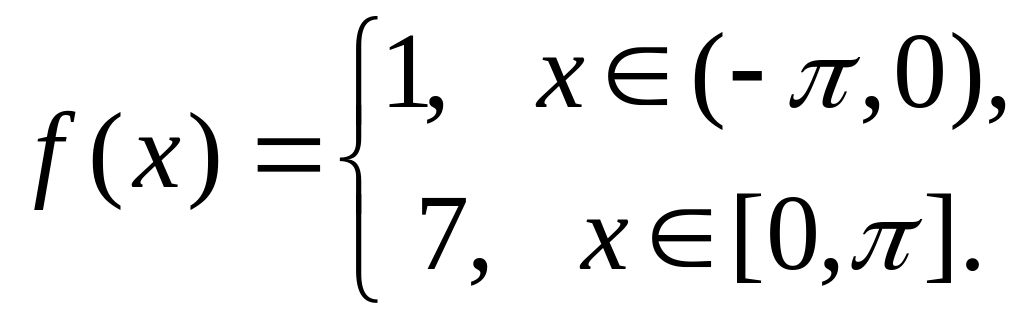Вариант 10
Исследовать сходимость рядов 1)
,
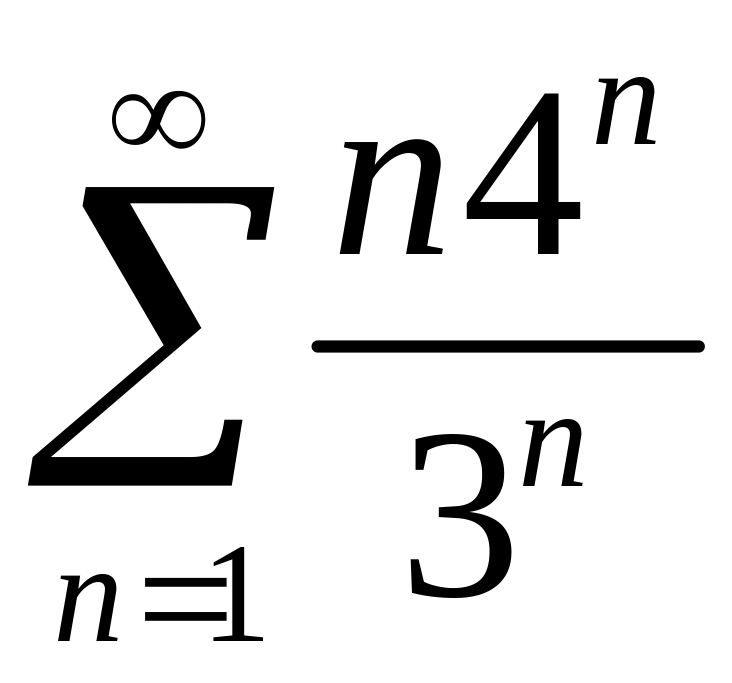2)
.
Исследовать сходимость знакопеременных рядов
1)
,
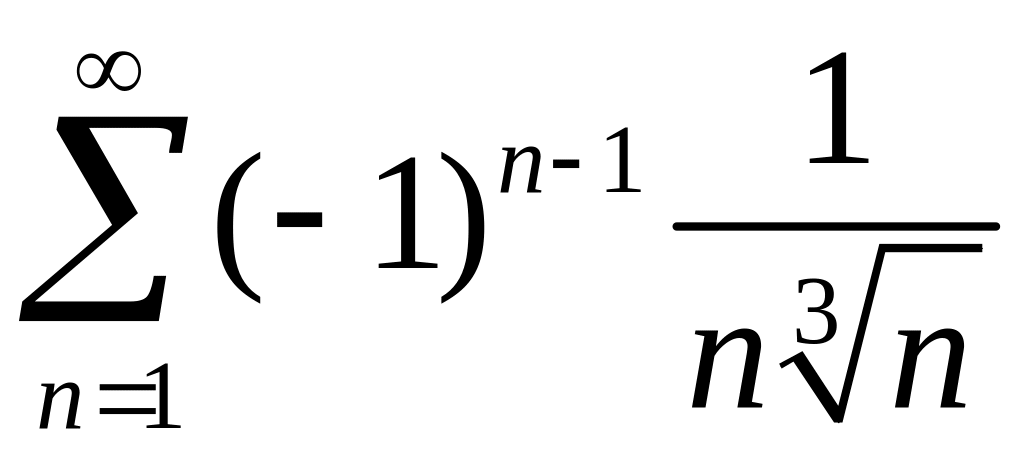2)
.
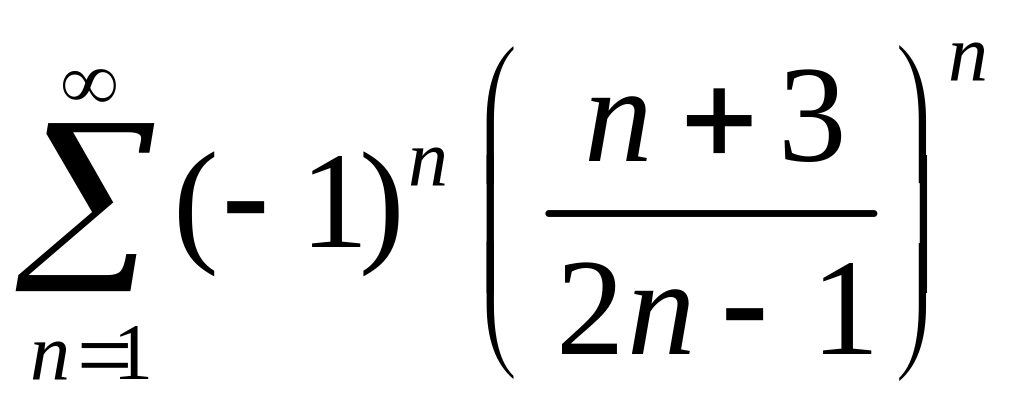Найти область сходимости степенного ряда
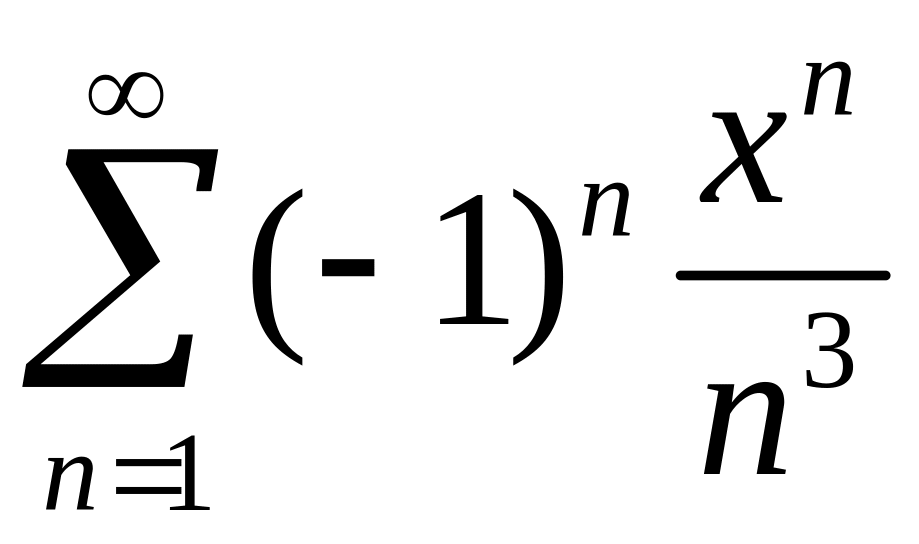.Функцию
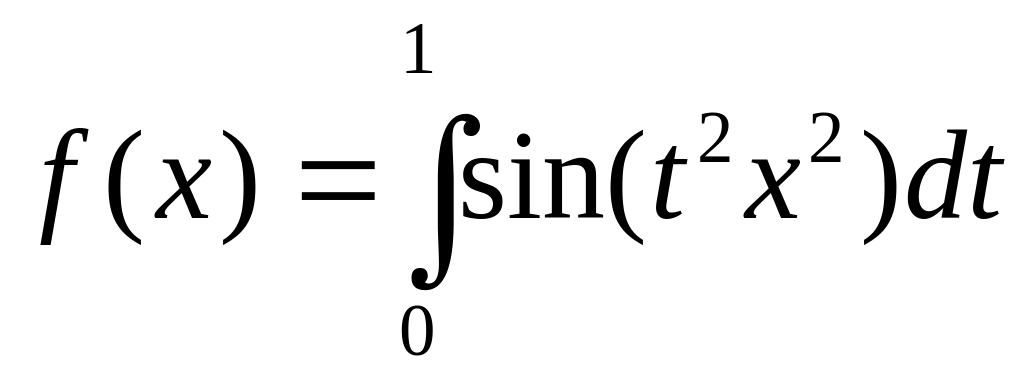разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
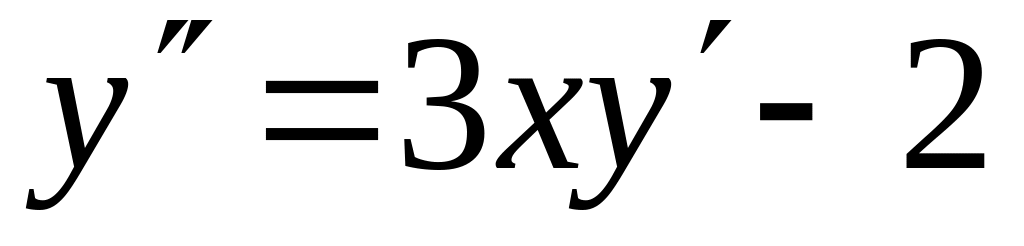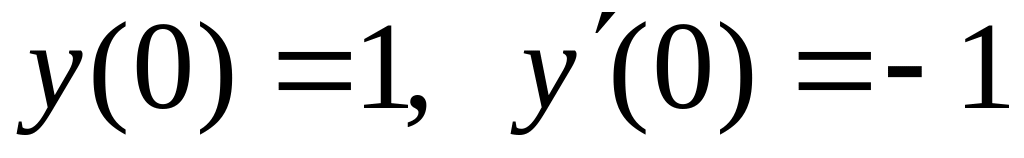.Разложить в ряд Фурье .
Вариант 11
Исследовать сходимость рядов 1)
,
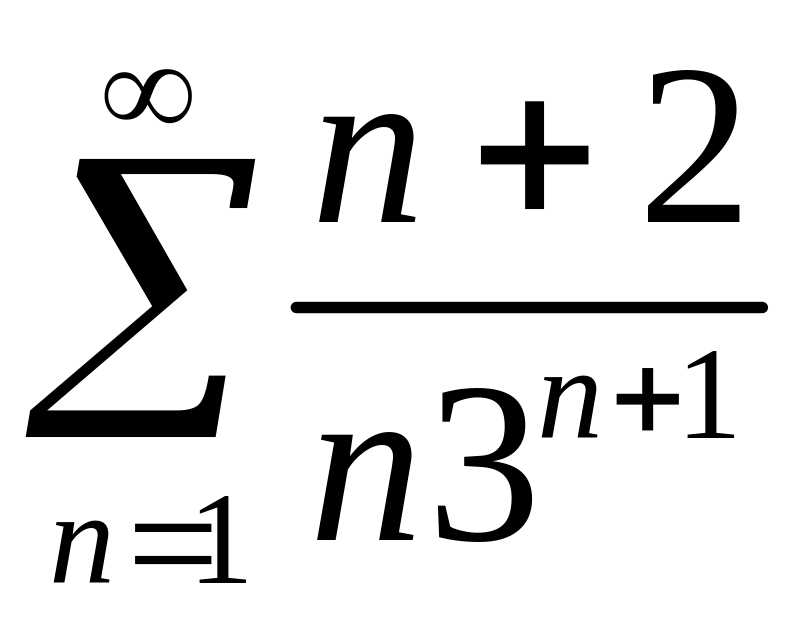2)
.
Исследовать сходимость знакопеременных рядов
1)
,
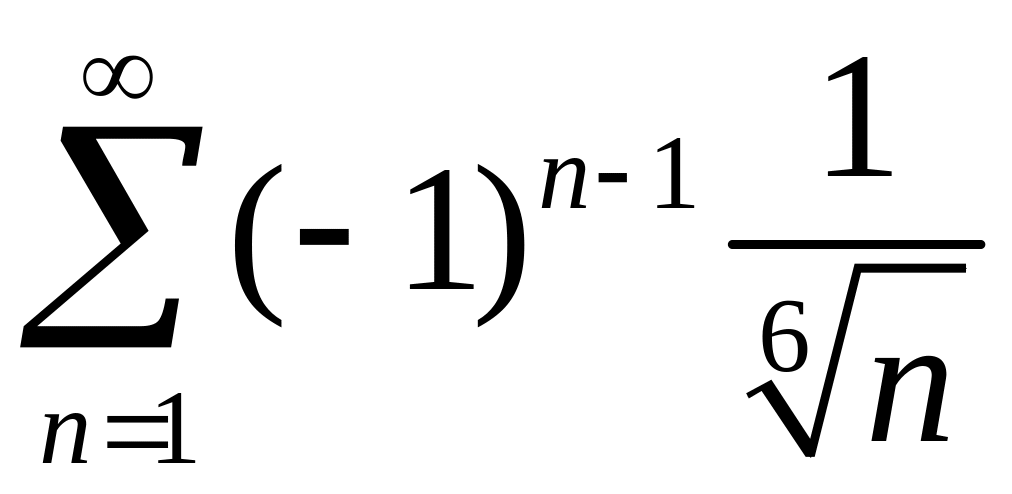2)
.
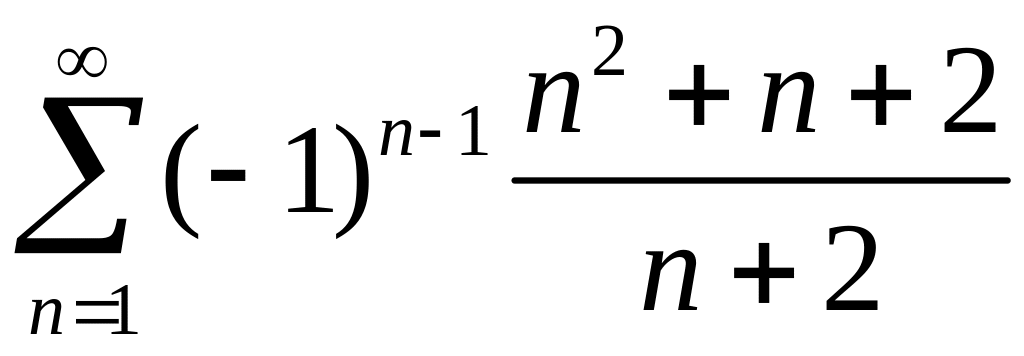Найти область сходимости степенного ряда .
Функцию
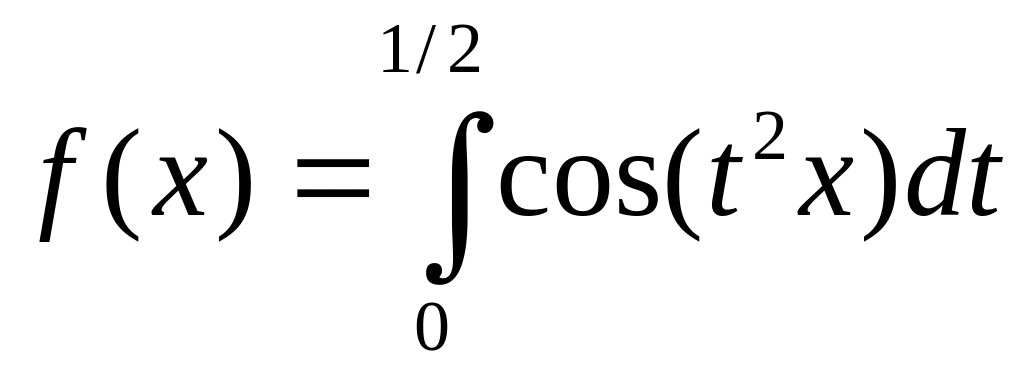разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
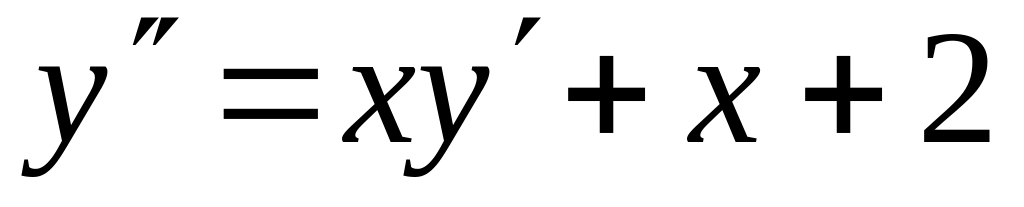.Разложить в ряд Фурье
Вариант 12
Исследовать сходимость рядов 1)
,
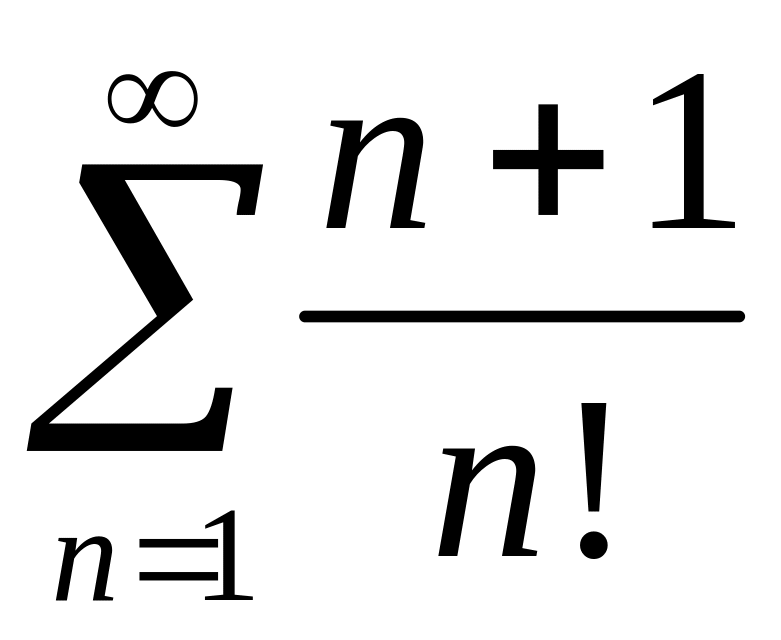2)
.
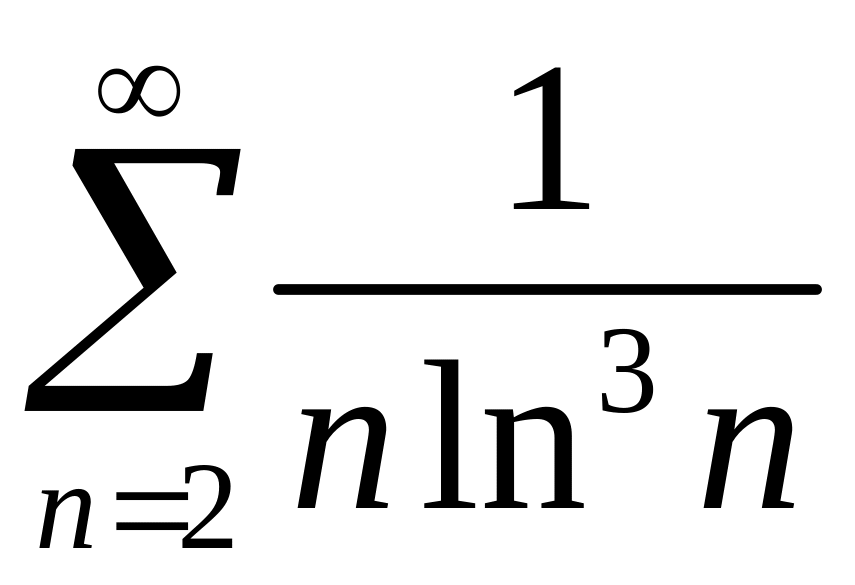Исследовать сходимость знакопеременных рядов
1)
,
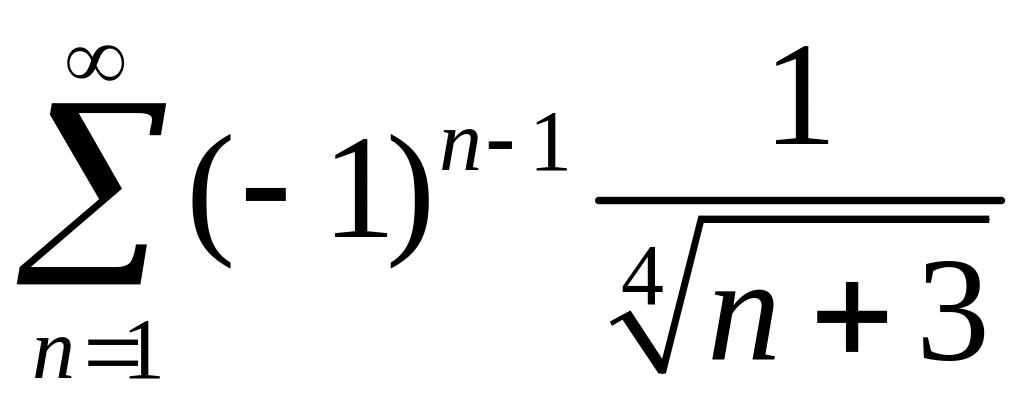2)
.
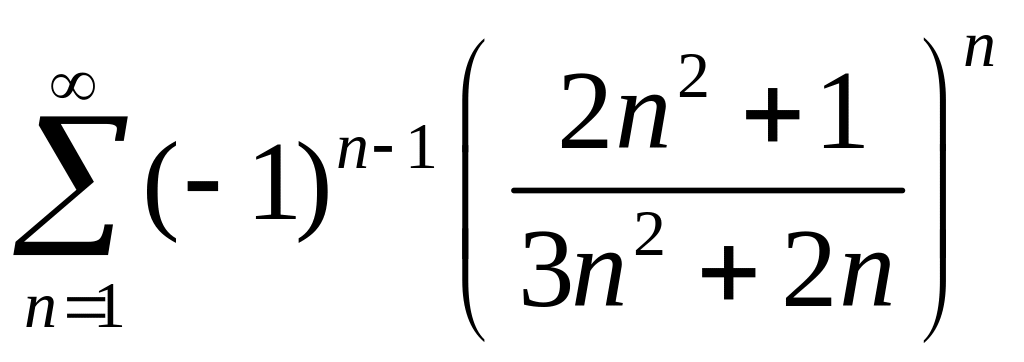Найти область сходимости степенного ряда
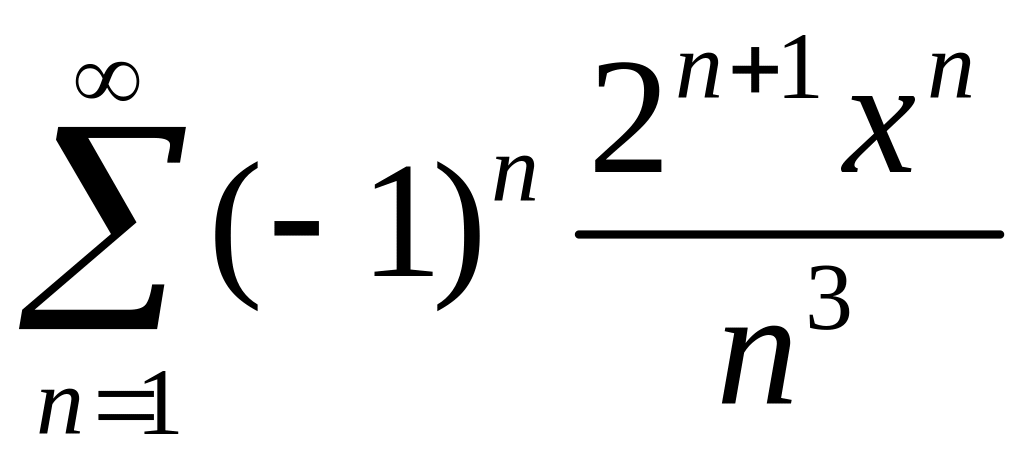.Функцию
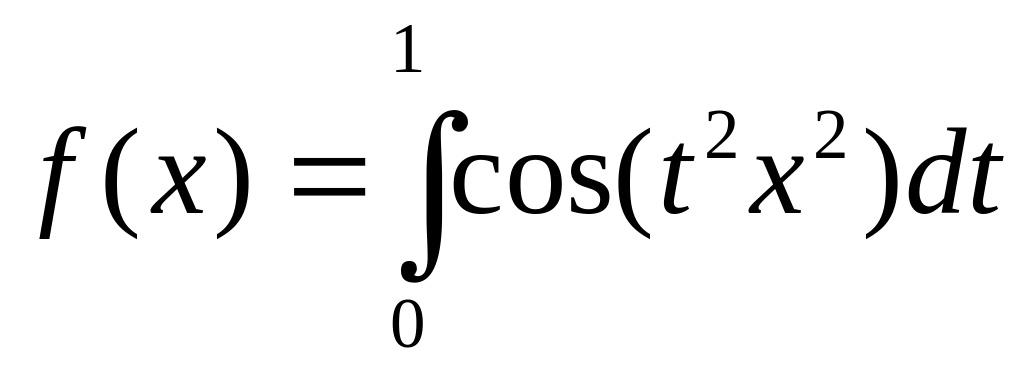разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
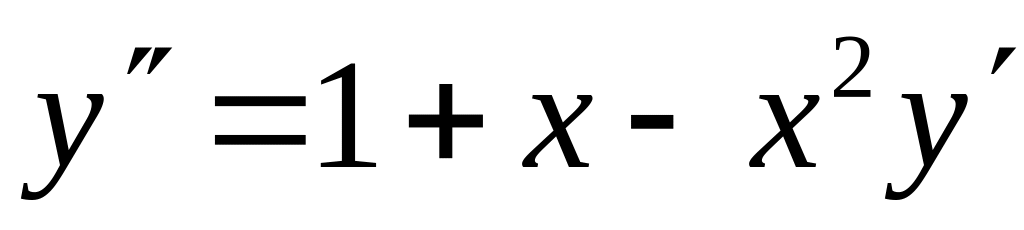.Разложить в ряд Фурье
.
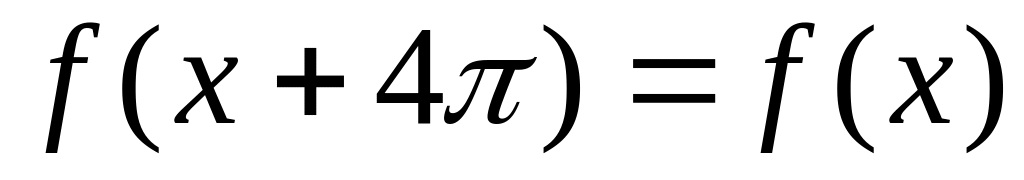Вариант 13
Исследовать сходимость рядов 1)
,
2)
.
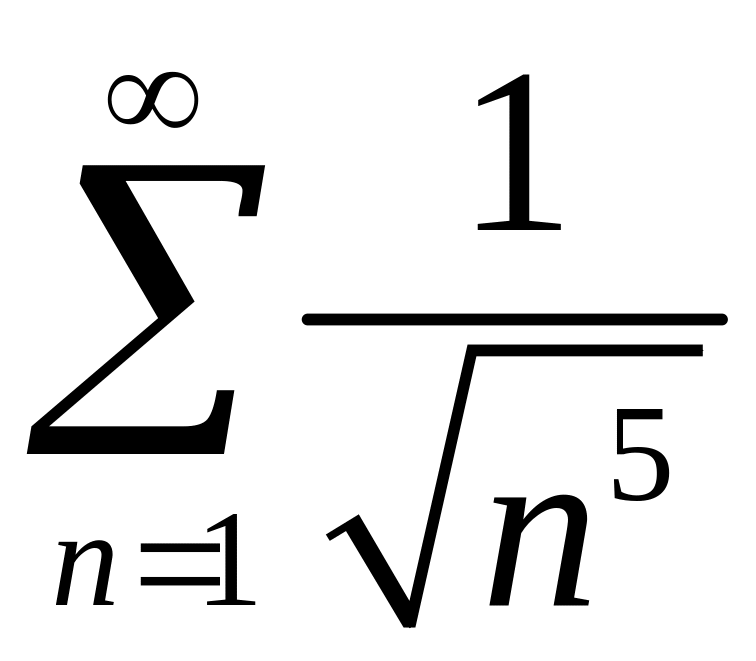Исследовать сходимость знакопеременных рядов
1)
,
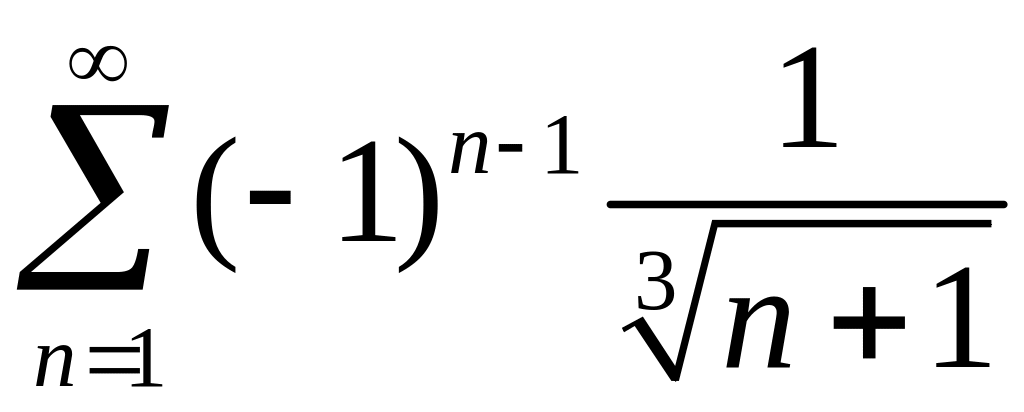2)
.
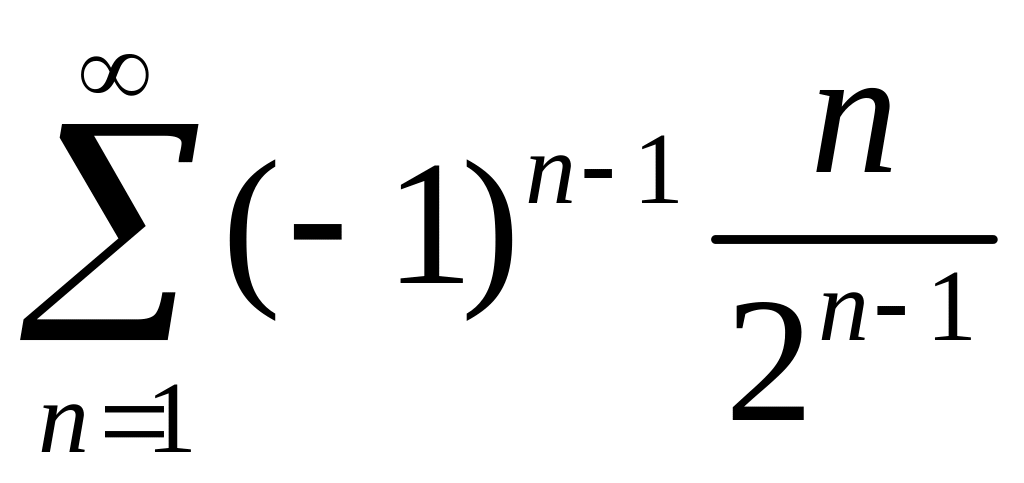Найти область сходимости степенного ряда
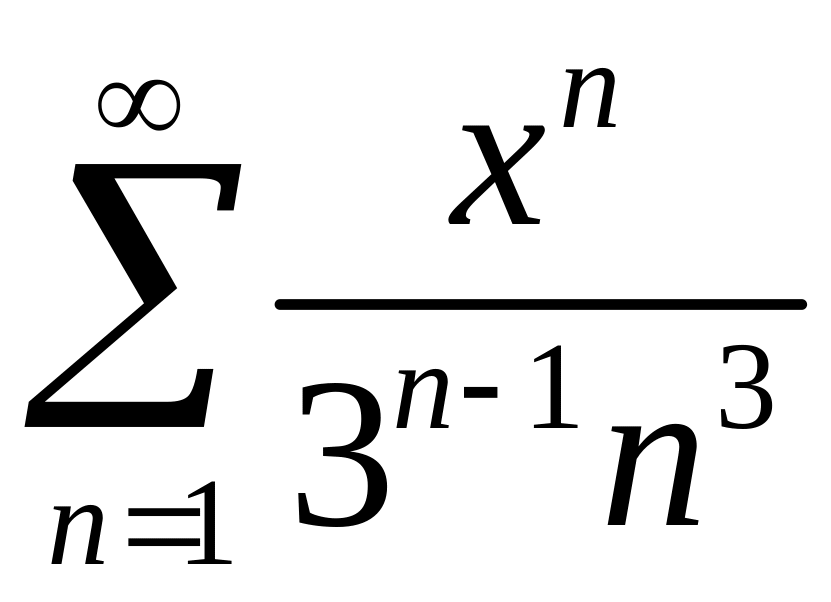.Функцию
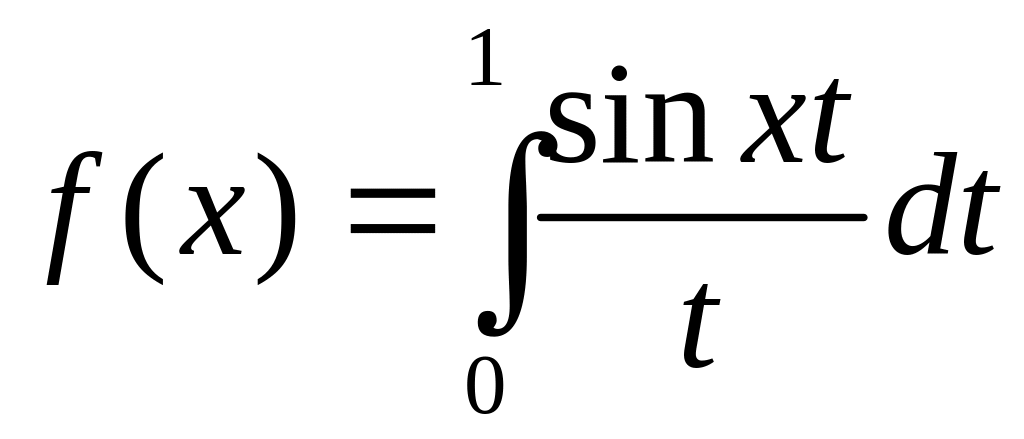разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
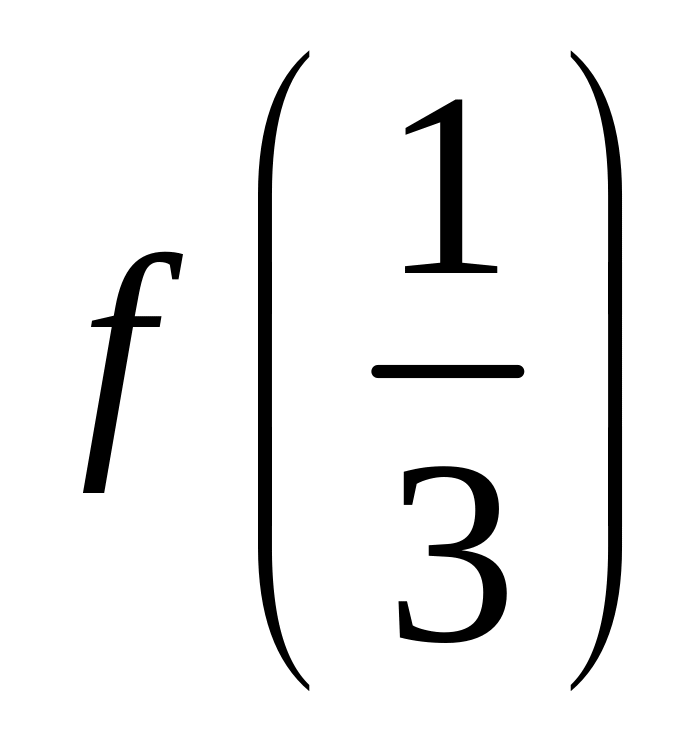с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
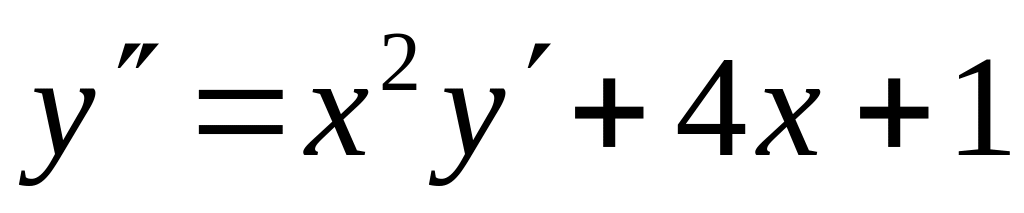.Разложить в ряд Фурье
.
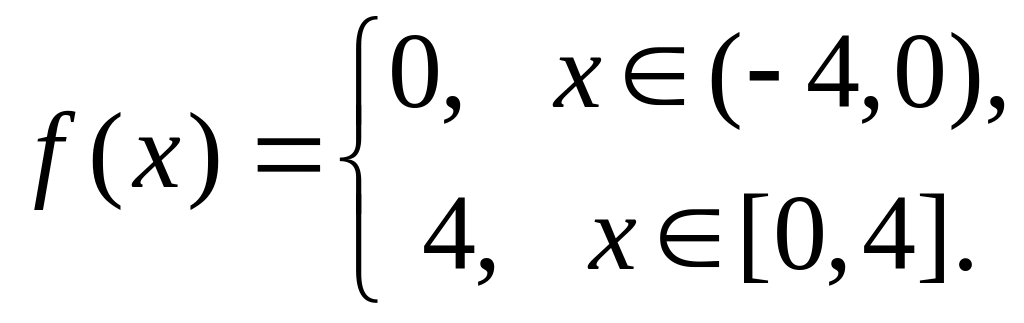
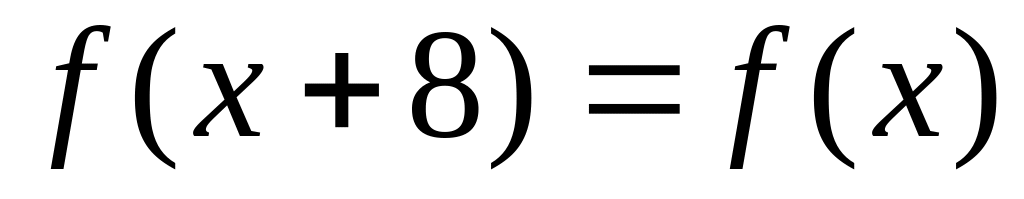Вариант 14
Исследовать сходимость рядов 1)
,
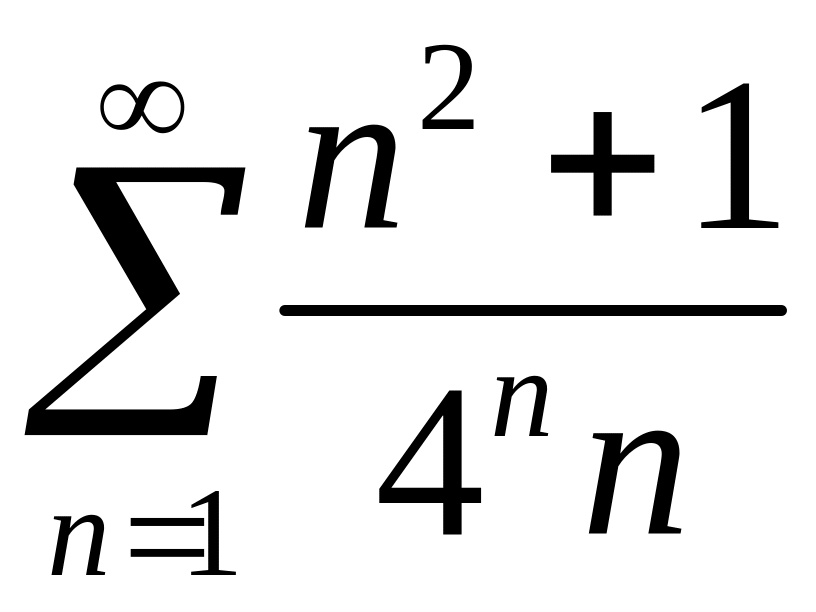2)
.
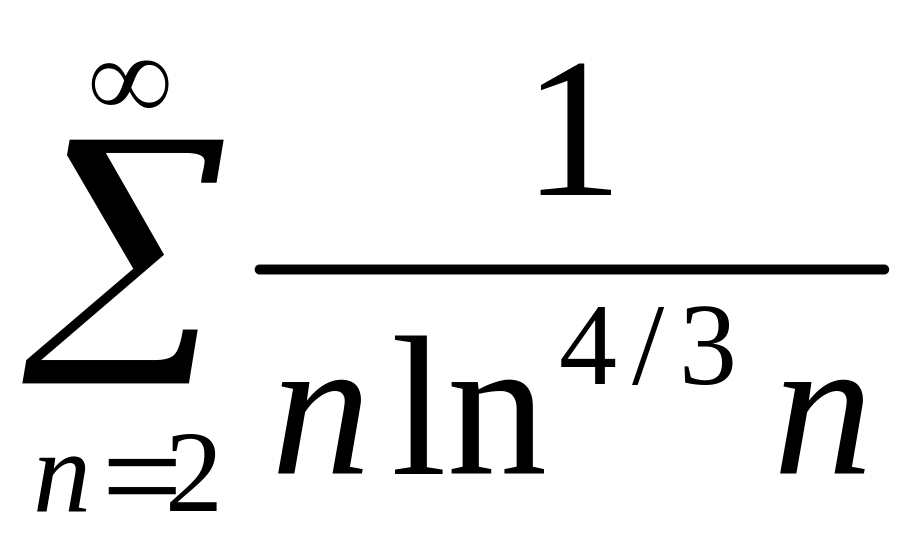Исследовать сходимость знакопеременных рядов
1)
,
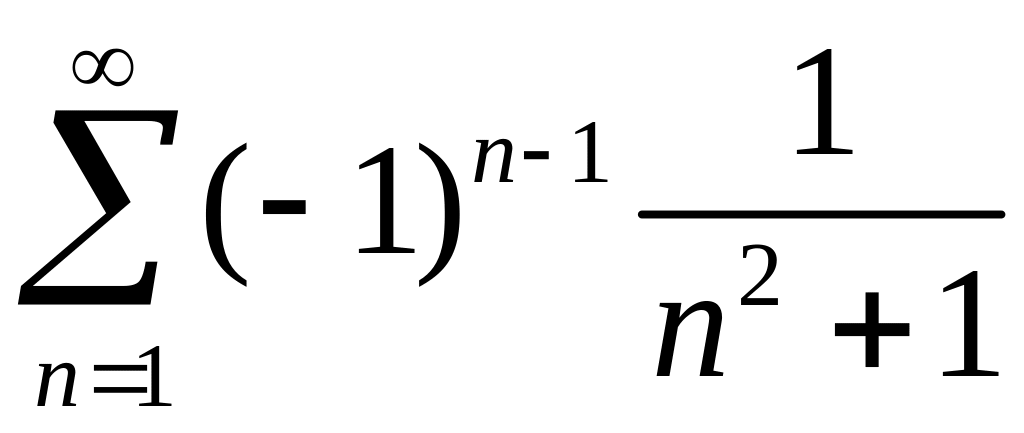2)
.
Найти область сходимости степенного ряда
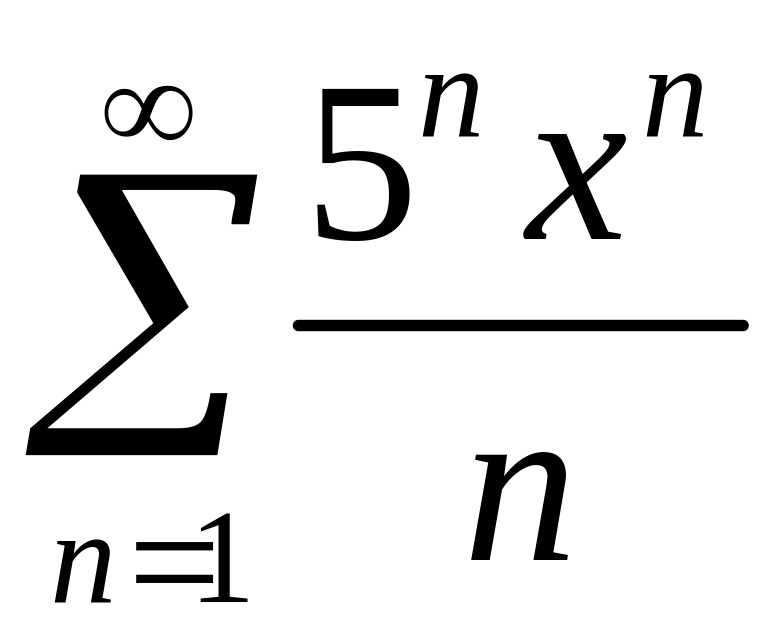.Функцию
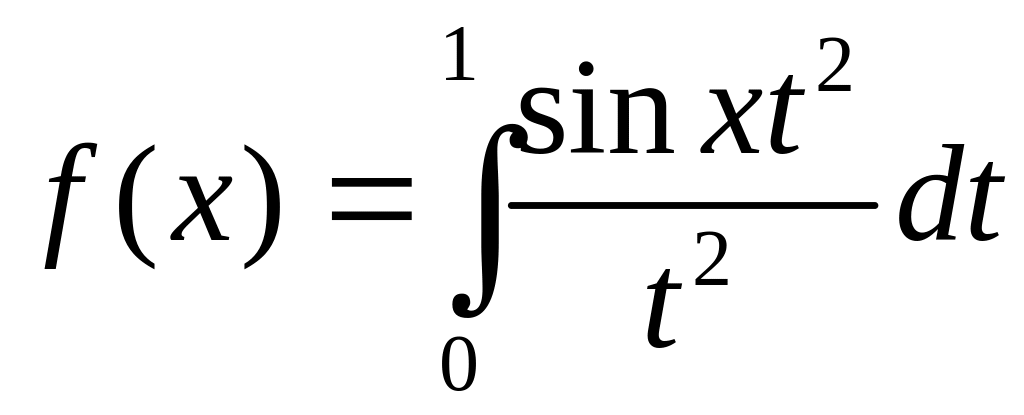разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
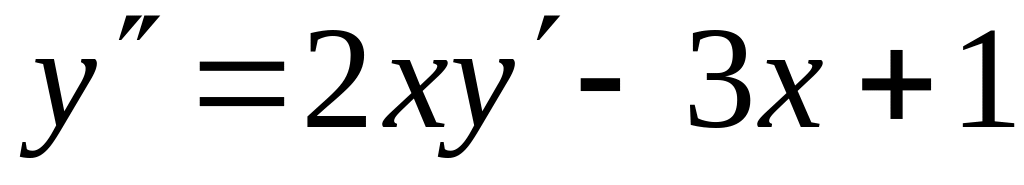.Разложить в ряд Фурье
.
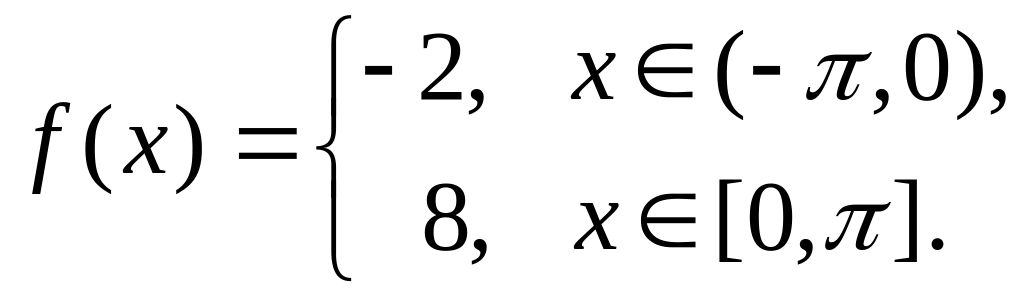Вариант 15
Исследовать сходимость рядов 1)
,
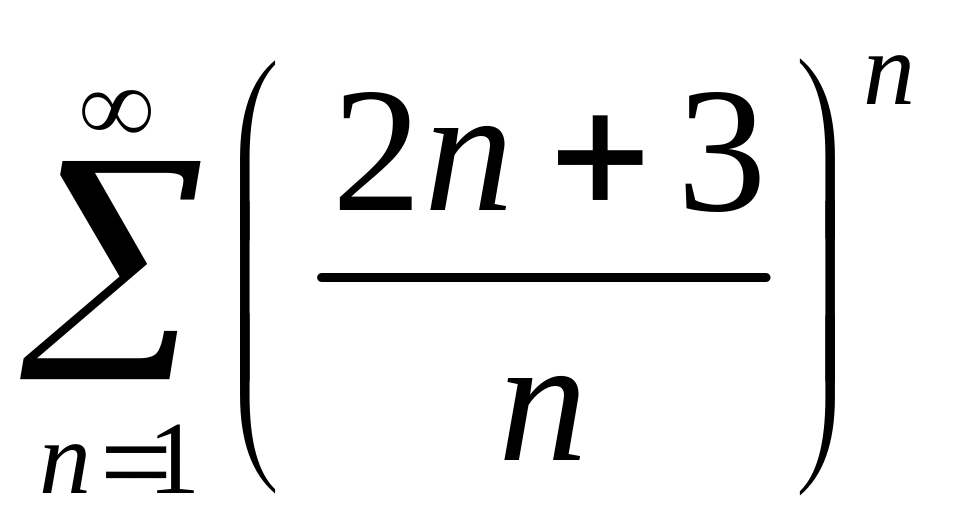2)
.
Исследовать сходимость знакопеременных рядов
1)
,
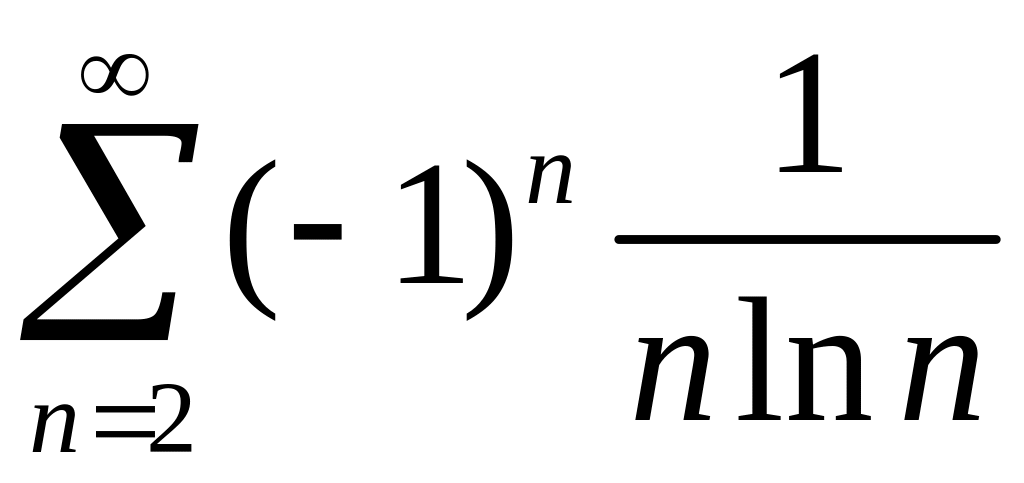2)
.
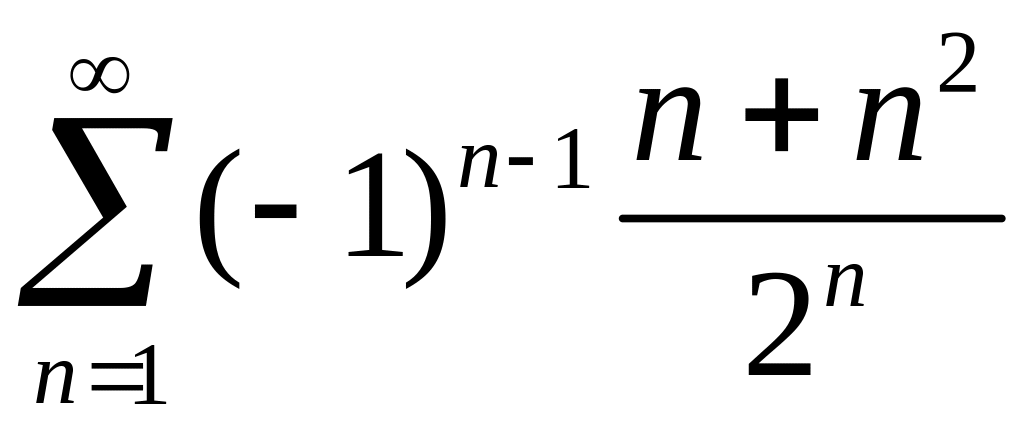Найти область сходимости степенного ряда
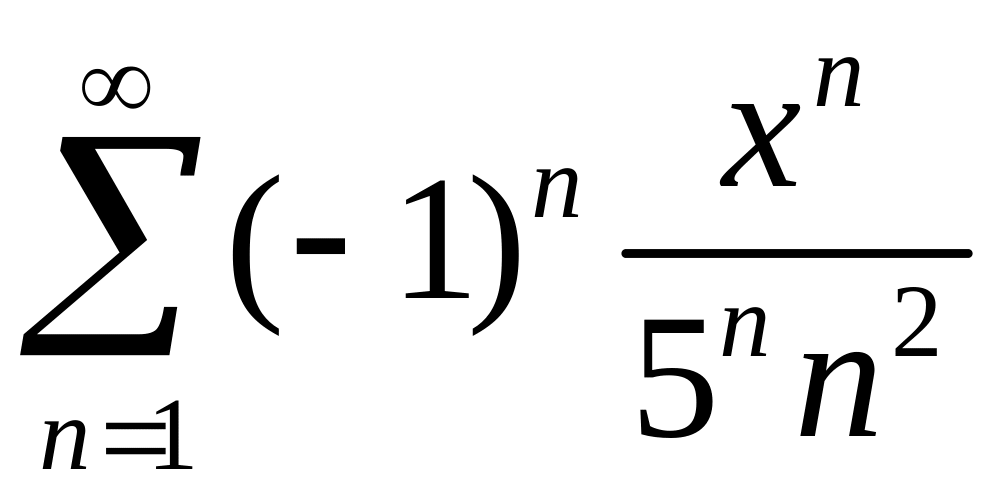.Функцию
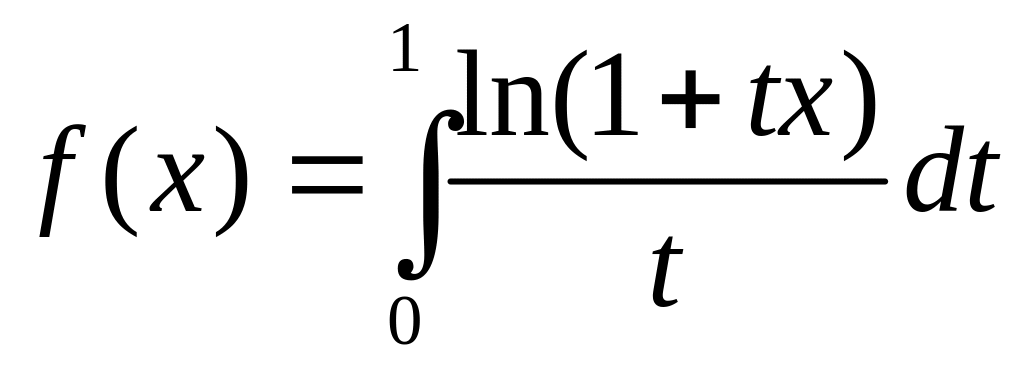разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
.Разложить в ряд Фурье
Вариант 16
Исследовать сходимость рядов 1)
,
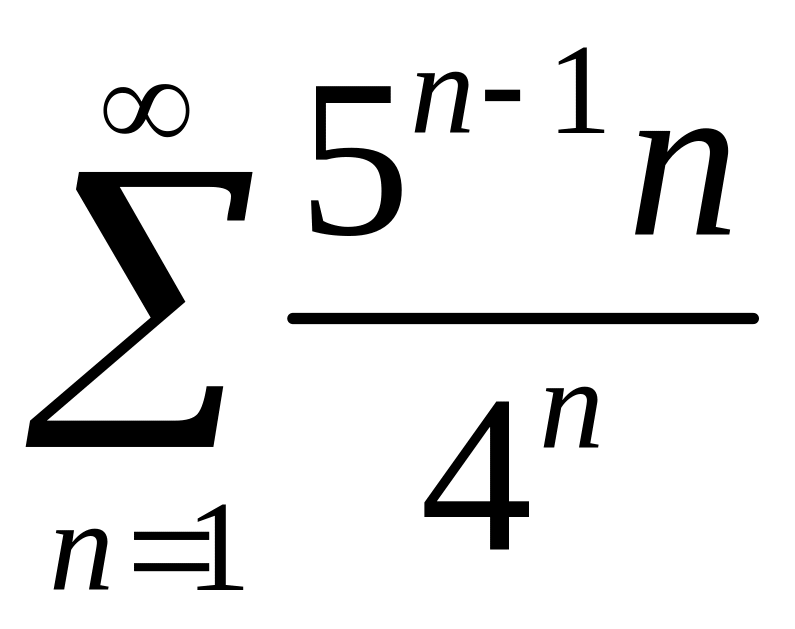2)
.
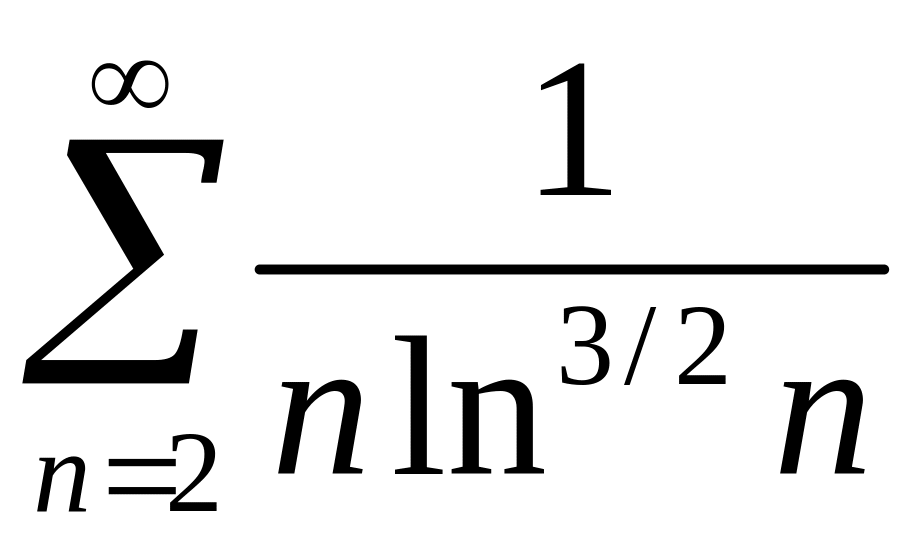Исследовать сходимость знакопеременных рядов
1) , 2) .
Найти область сходимости степенного ряда .
Функцию
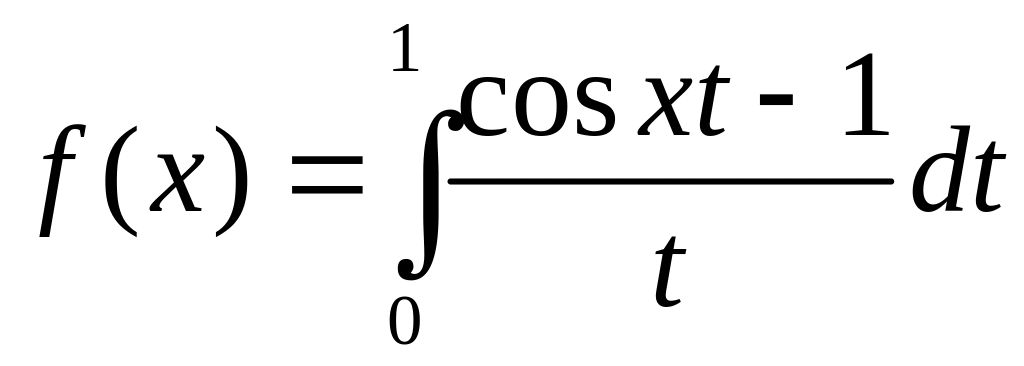разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения , .
Разложить в ряд Фурье
.
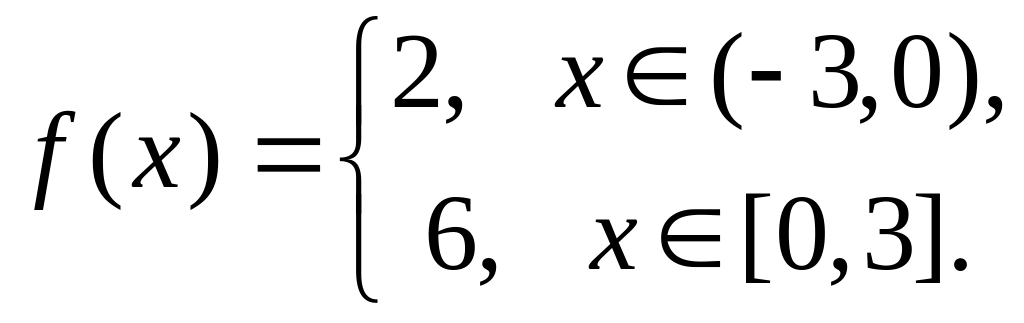
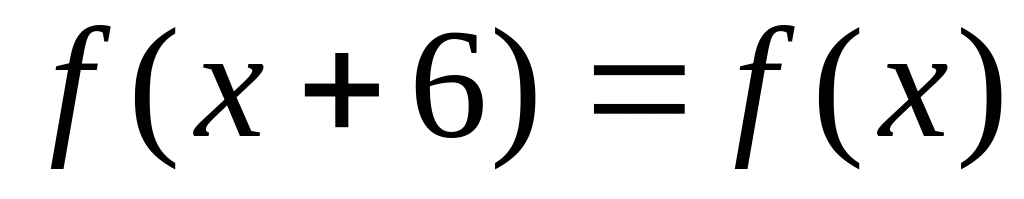Вариант 17
Исследовать сходимость рядов 1)
,
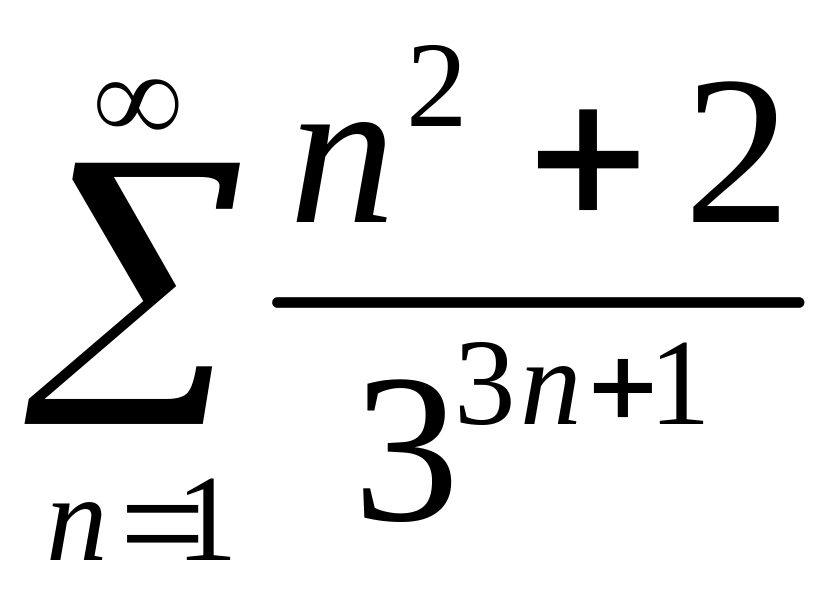2)
.
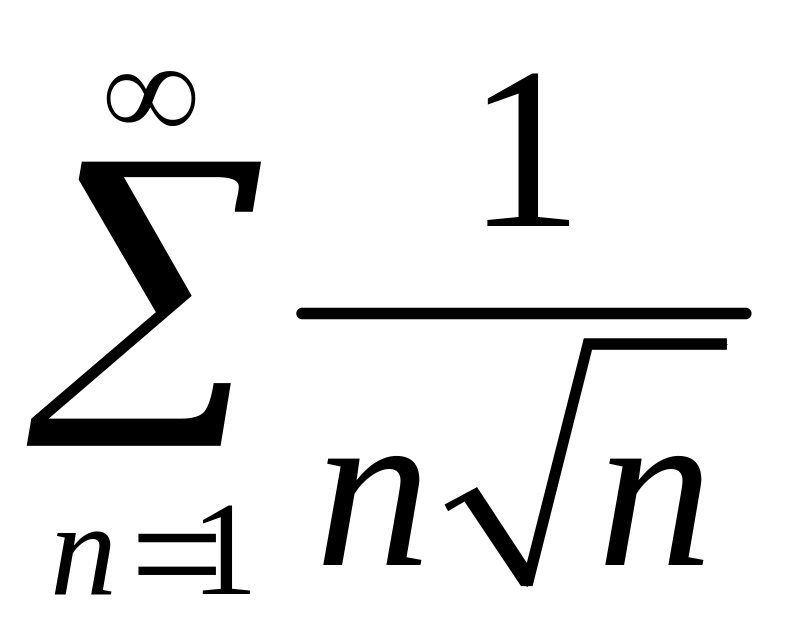Исследовать сходимость знакопеременных рядов
1)
,
2)
.
Найти область сходимости степенного ряда
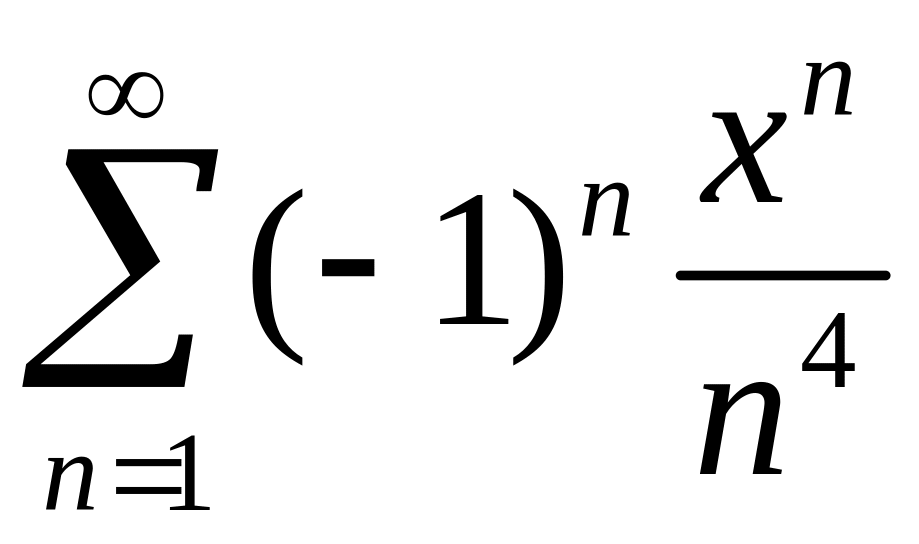.Функцию
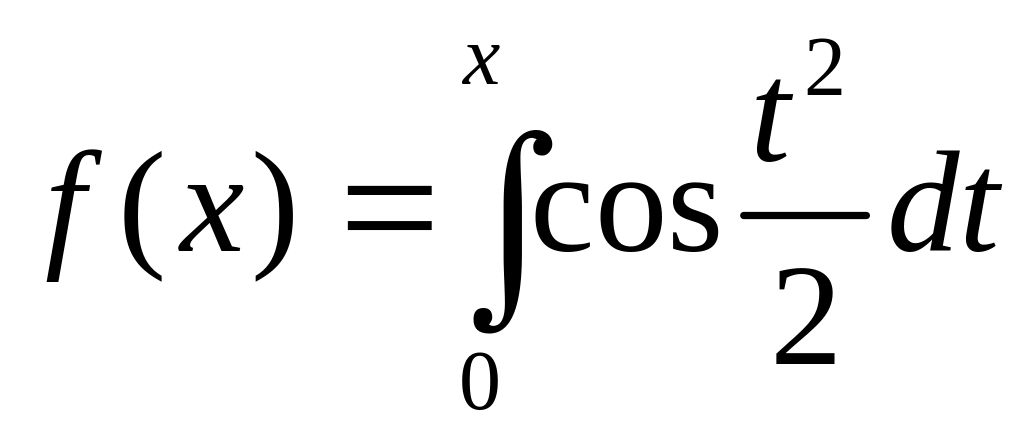разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
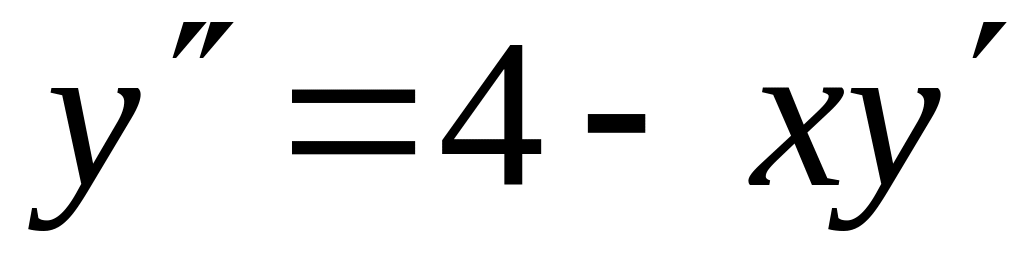.Разложить в ряд Фурье
.
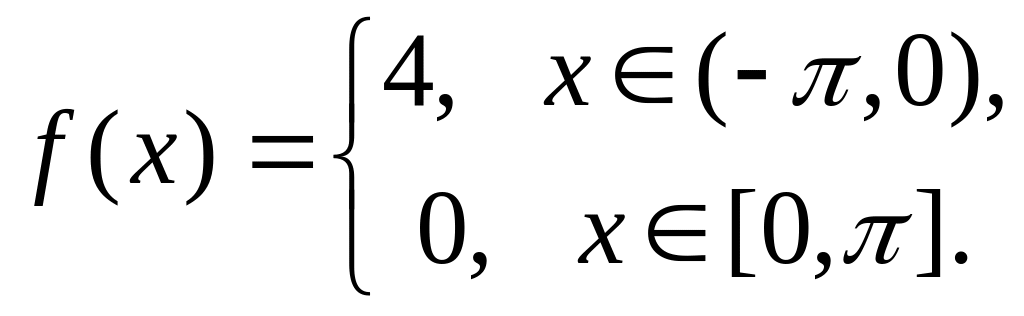Вариант 18
Исследовать сходимость рядов 1) , 2) .
Исследовать сходимость знакопеременных рядов
1) , 2) .
Найти область сходимости степенного ряда .
Функцию
разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
.Разложить в ряд Фурье
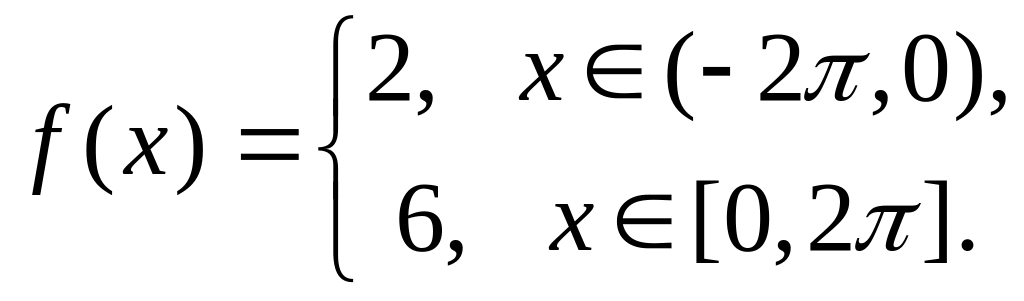
Вариант 19
Исследовать сходимость рядов 1)
,
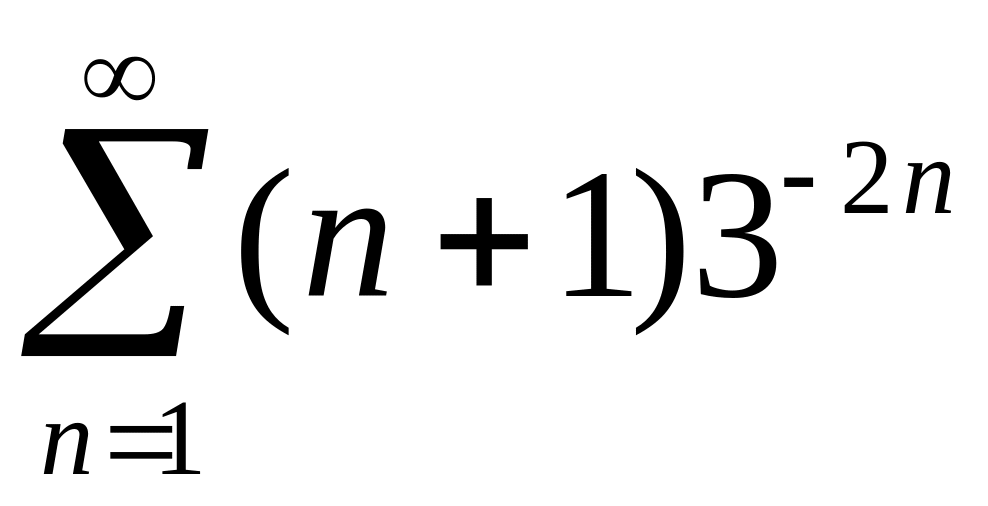2)
.
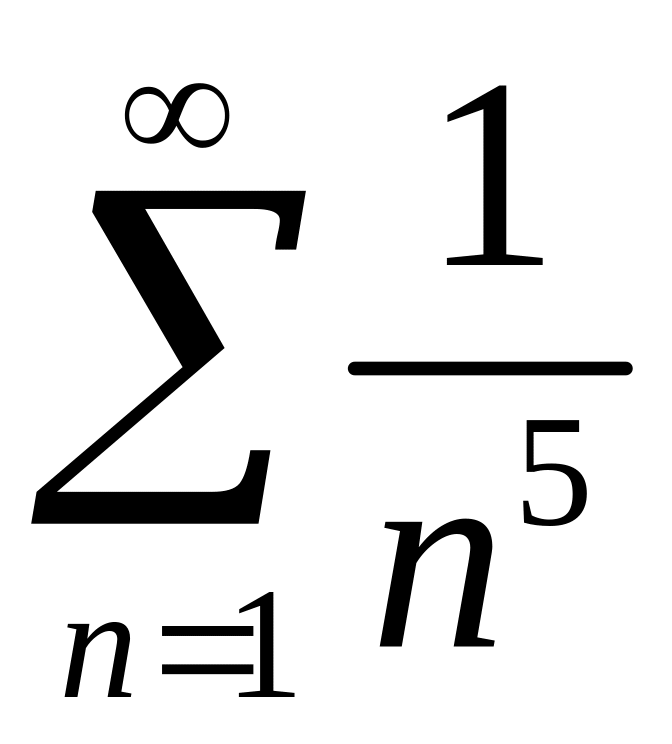Исследовать сходимость знакопеременных рядов
1)
,
2)
.
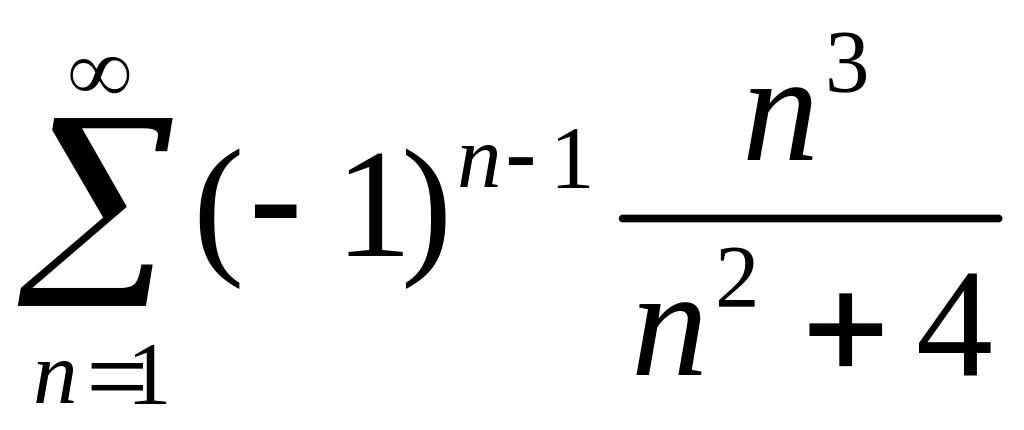Найти область сходимости степенного ряда
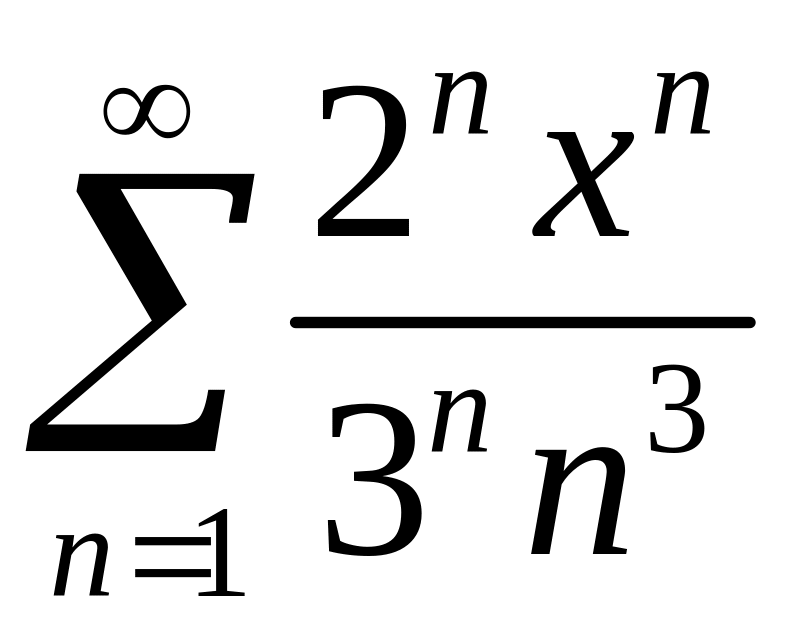.Функцию
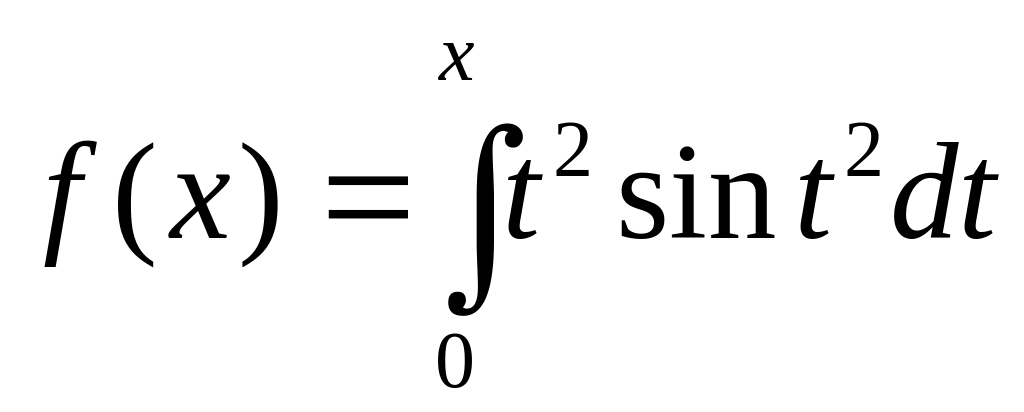разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
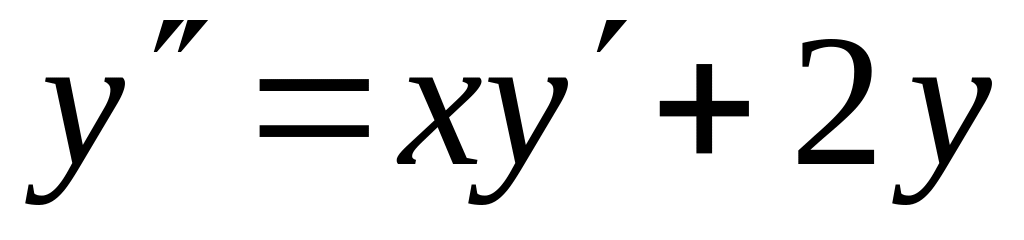.Разложить в ряд Фурье
.
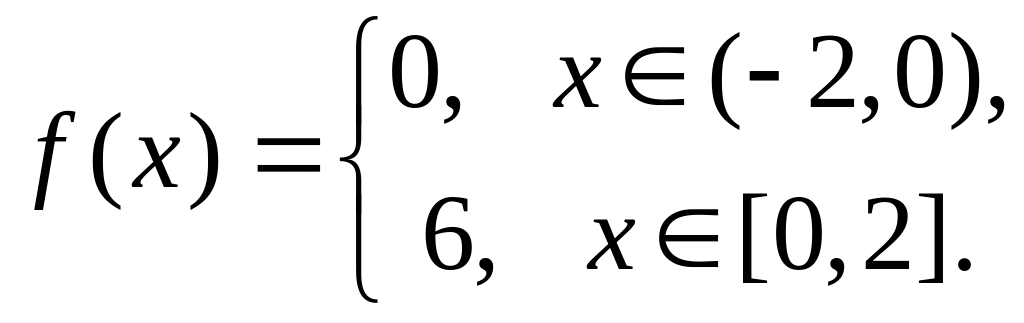Вариант 20
Исследовать сходимость рядов 1)
,
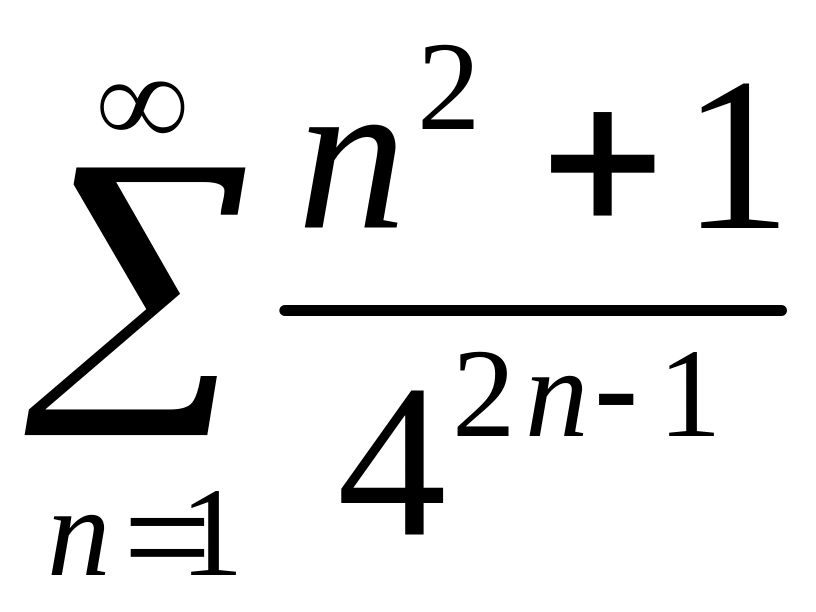2)
.
Исследовать сходимость знакопеременных рядов
1)
,
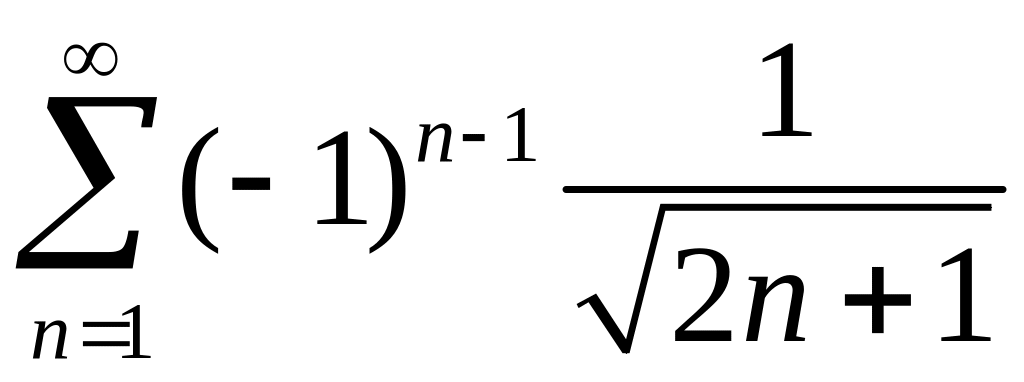2)
.
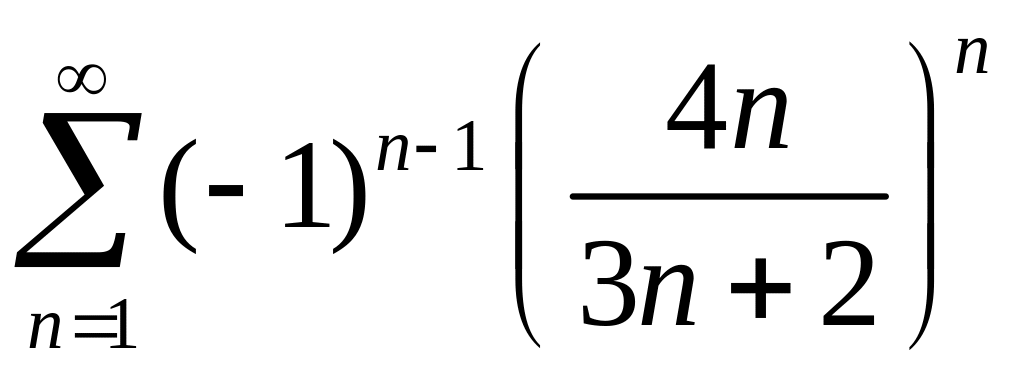Найти область сходимости степенного ряда
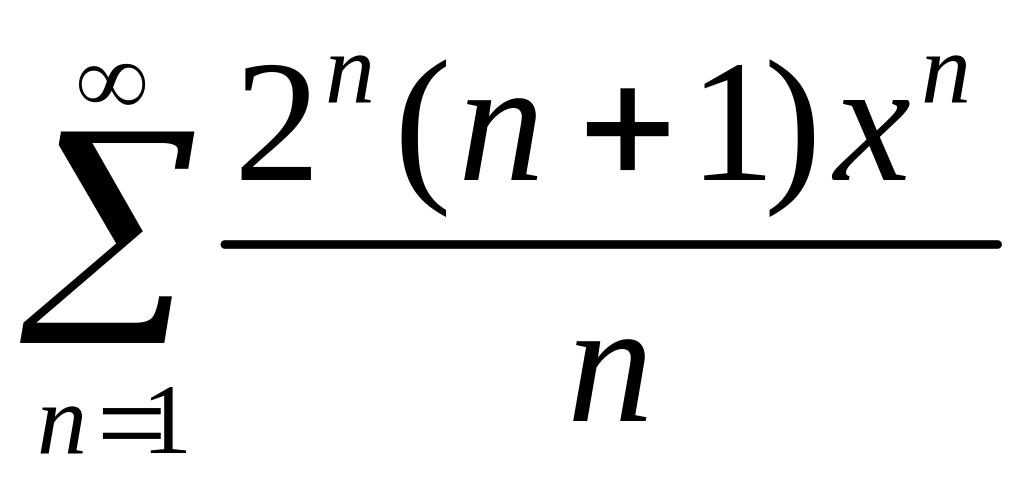.Функцию разложить в ряд по степеням x. Пользуясь полученным разложением, вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
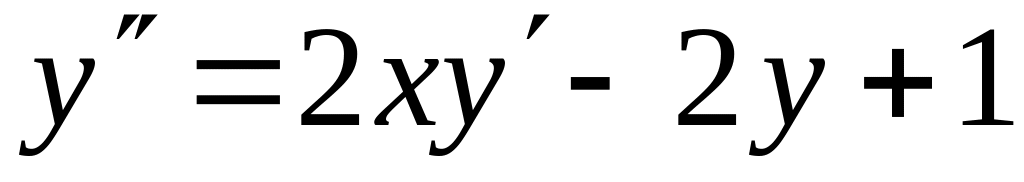.Разложить в ряд Фурье
.
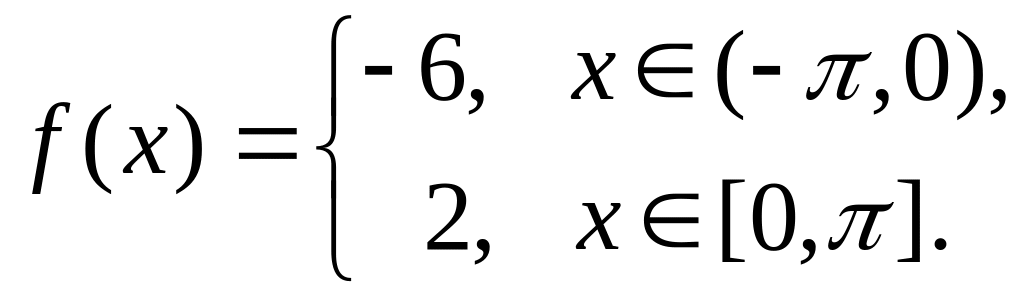Вариант 21
Исследовать сходимость рядов 1)
,
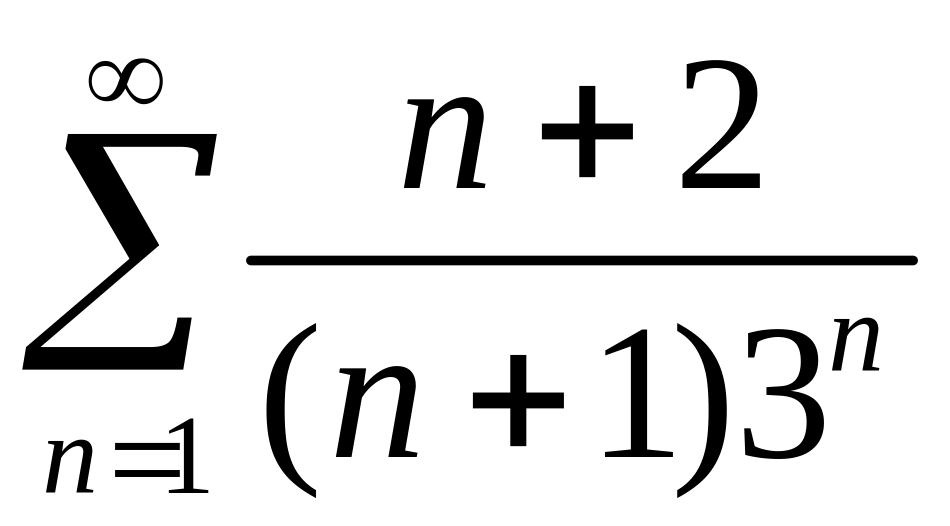2)
.
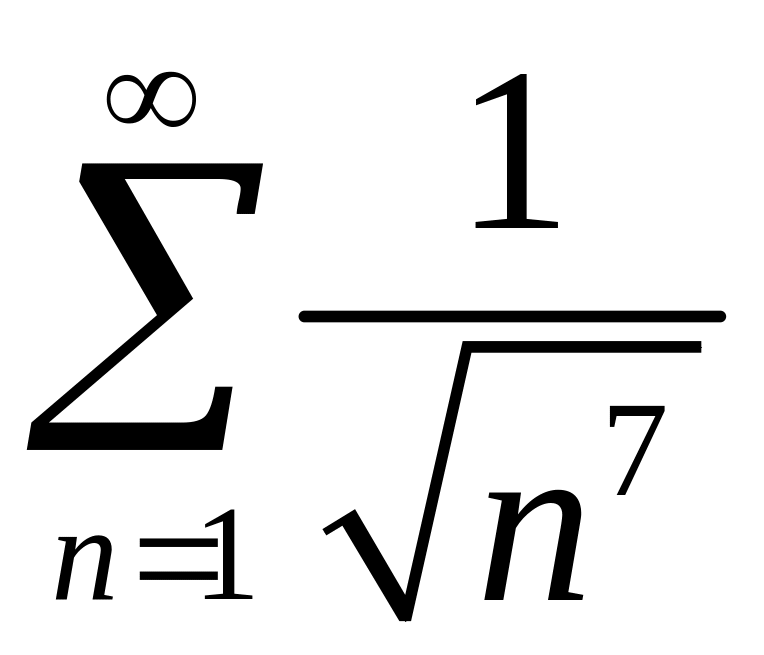Исследовать сходимость знакопеременных рядов
1)
,
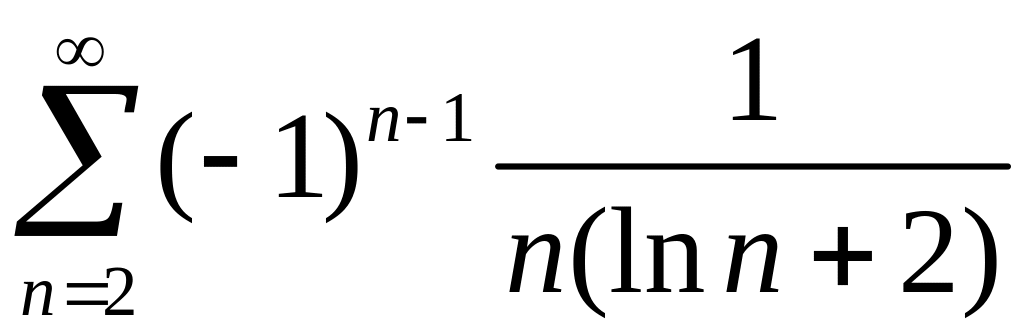2)
.
Найти область сходимости степенного ряда
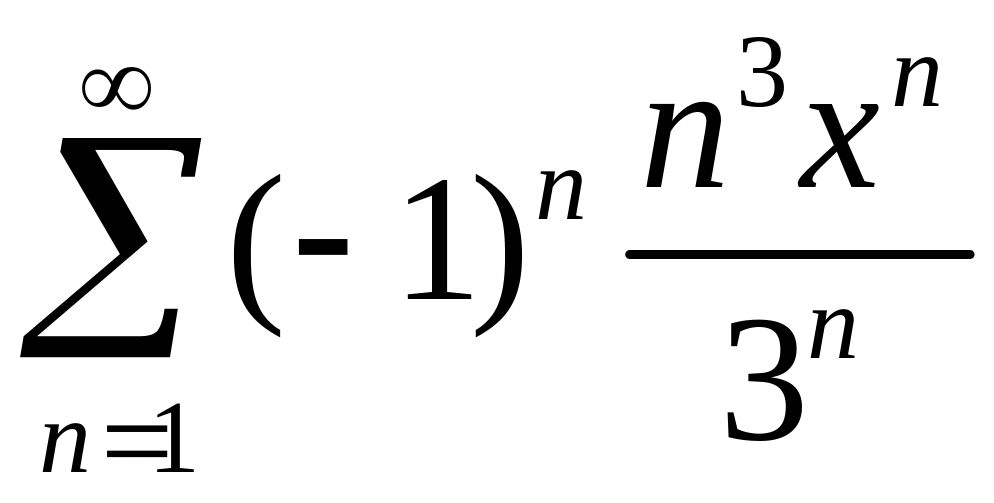.Функцию
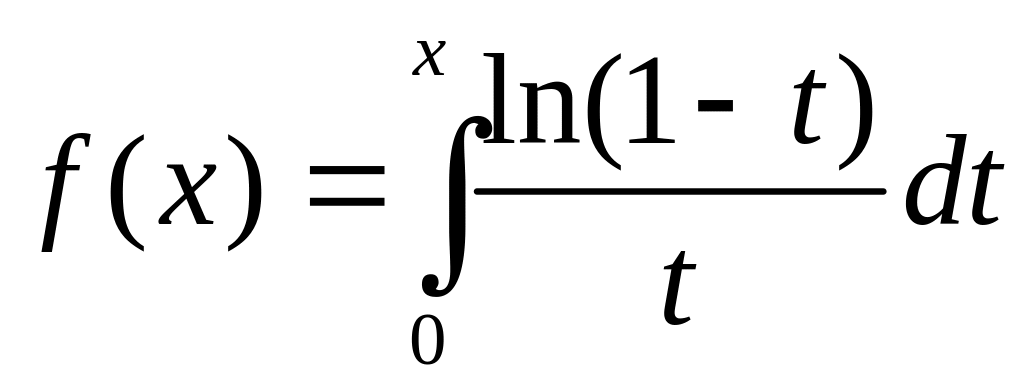разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
.Разложить в ряд Фурье
Вариант 22
Исследовать сходимость рядов 1)
,
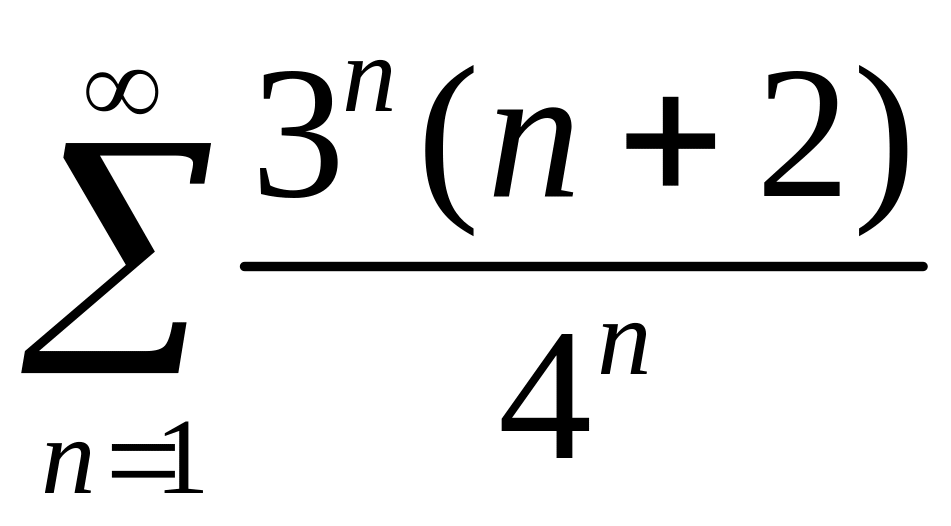2)
.
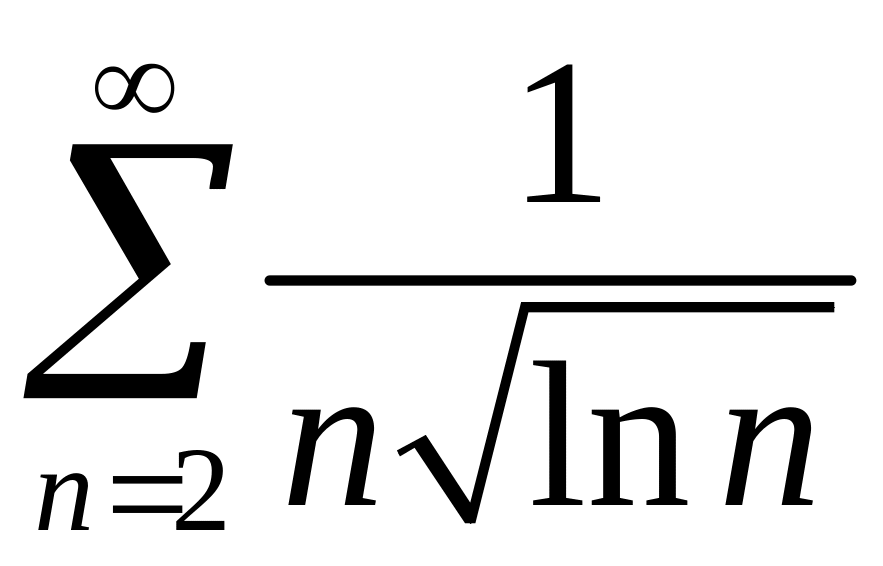Исследовать сходимость знакопеременных рядов
1)
,
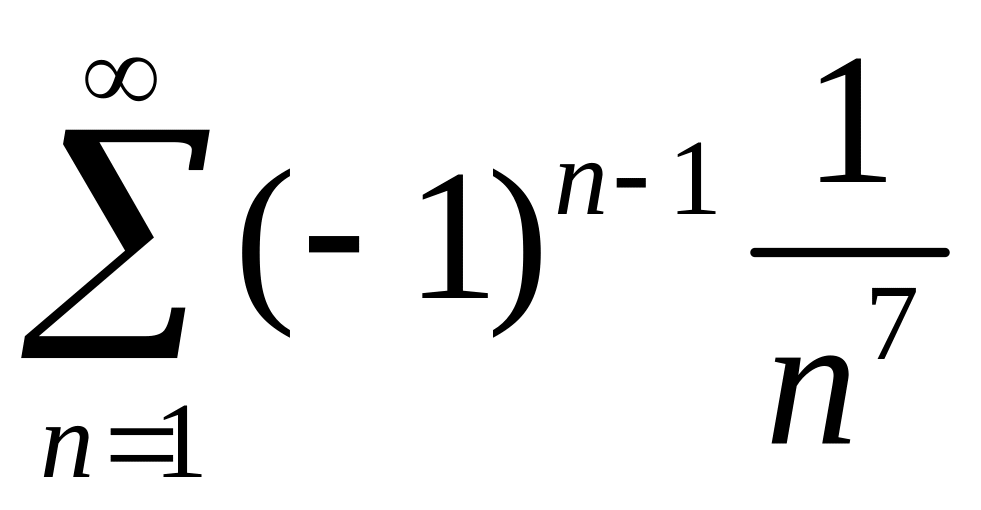2)
.
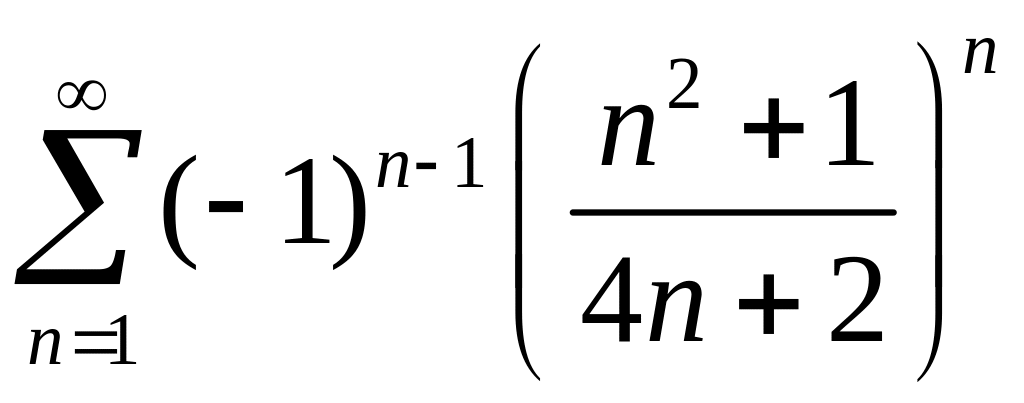Найти область сходимости степенного ряда
.Функцию
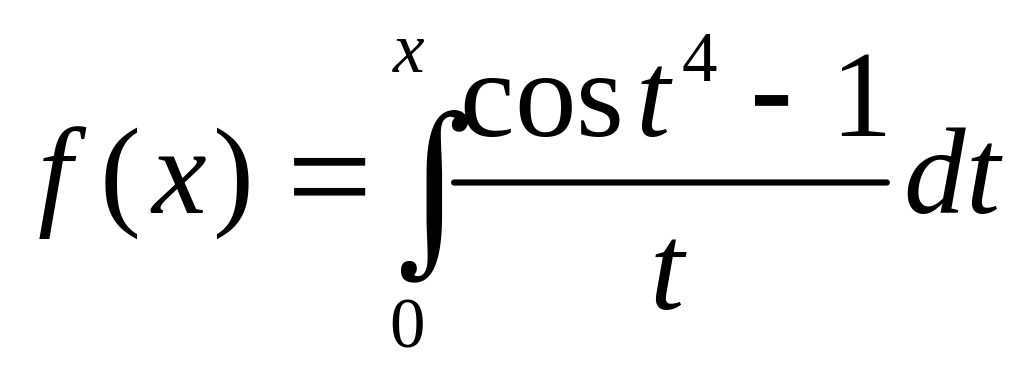разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
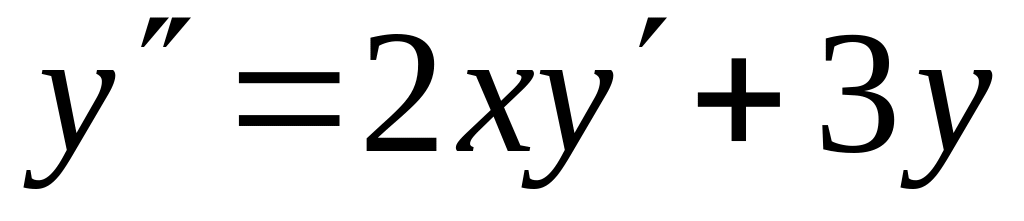.Разложить в ряд Фурье
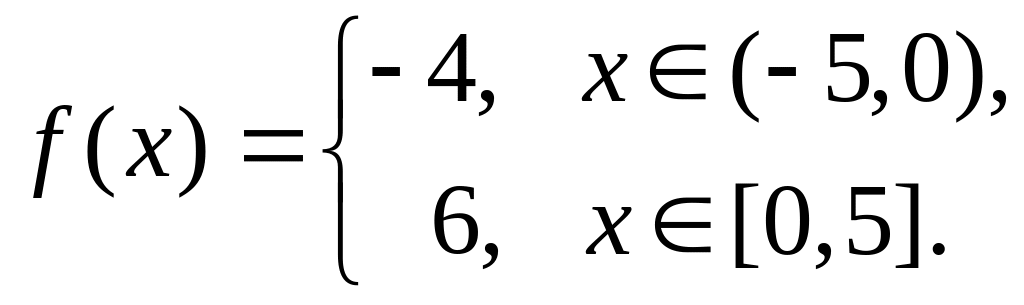
Вариант 23
1.
Исследовать
сходимость рядов 1)
,
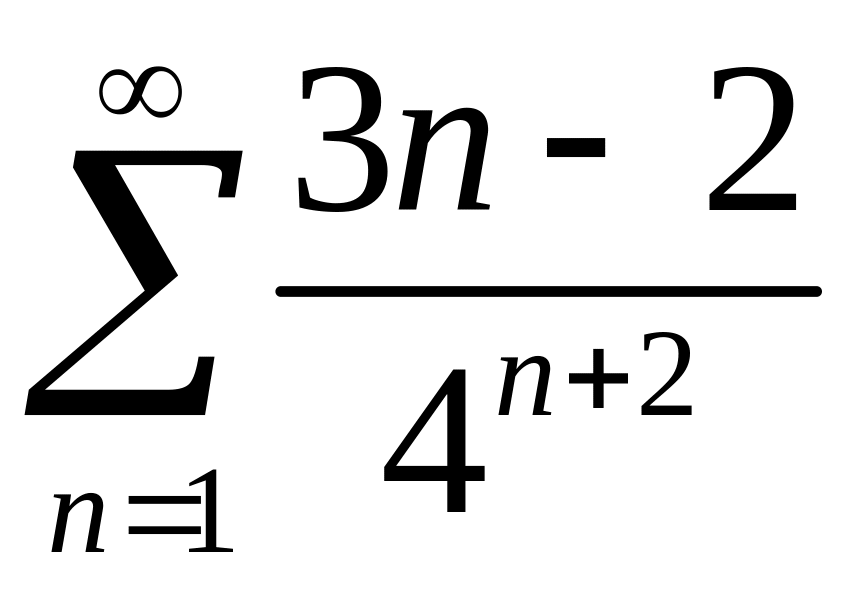2)
.
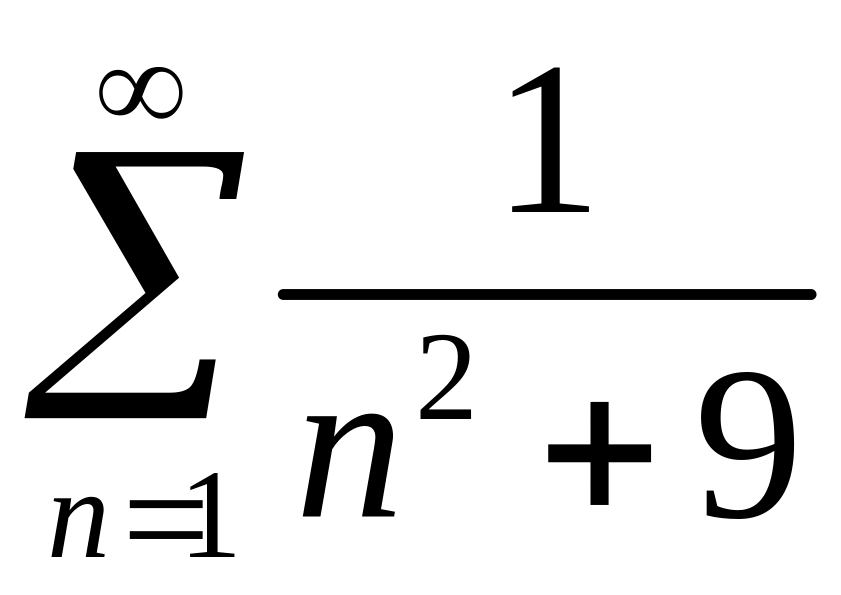Исследовать сходимость знакопеременных рядов
1)
,
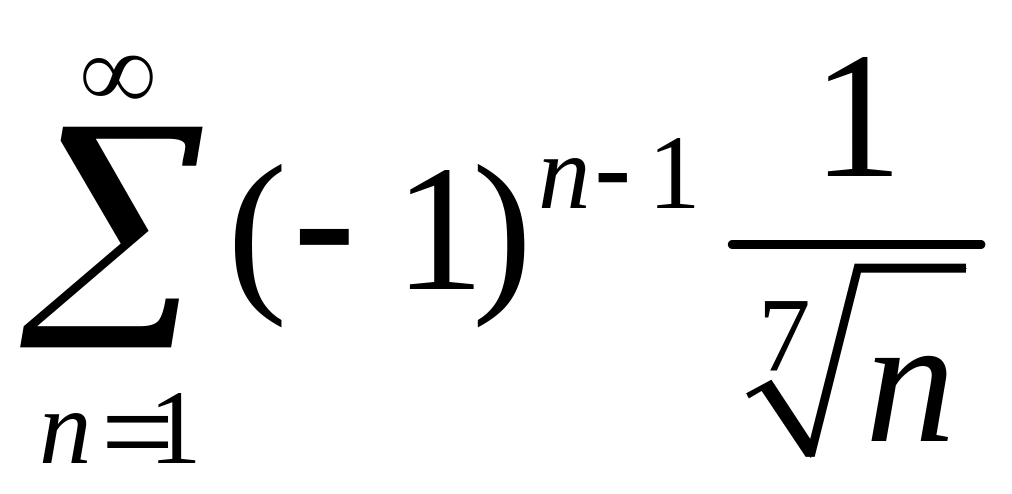2)
.
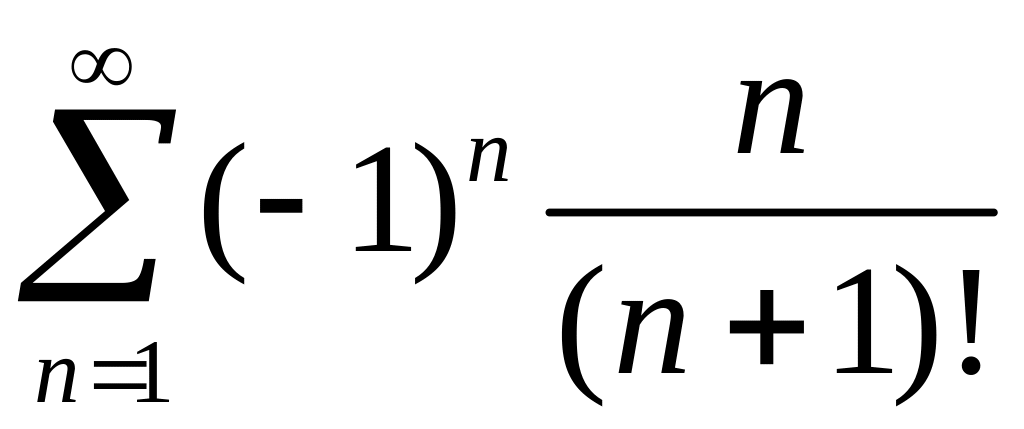Найти область сходимости степенного ряда
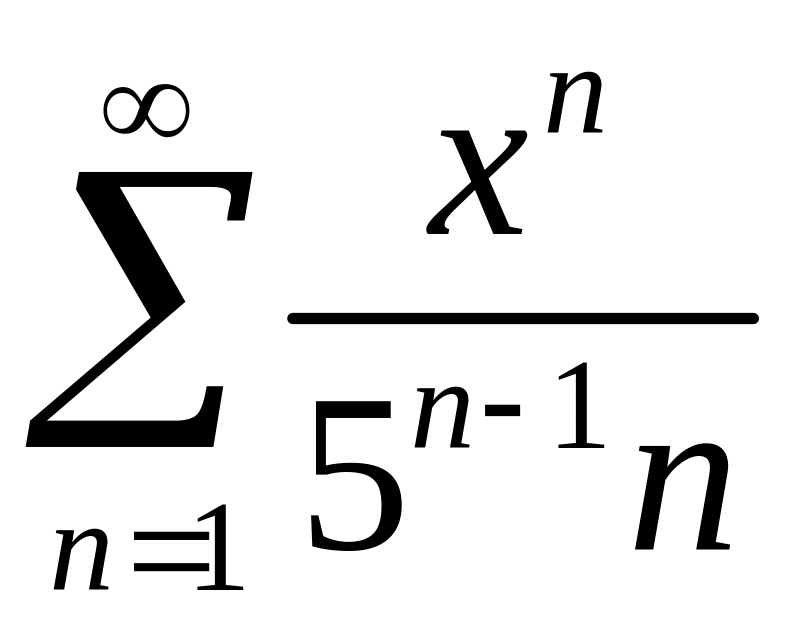.Функцию
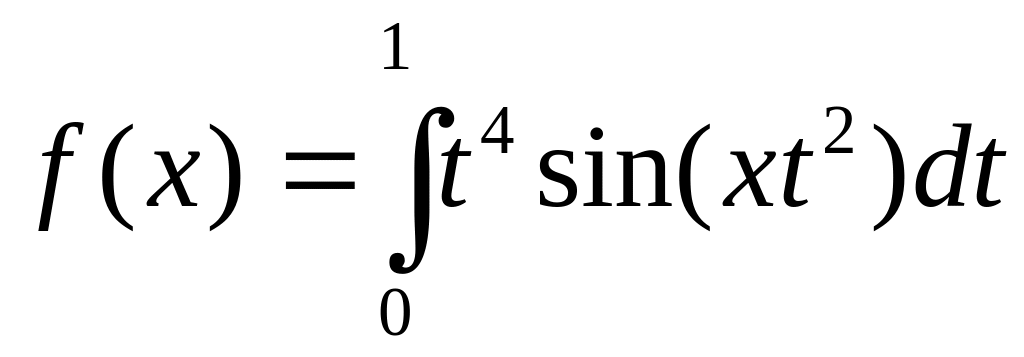разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
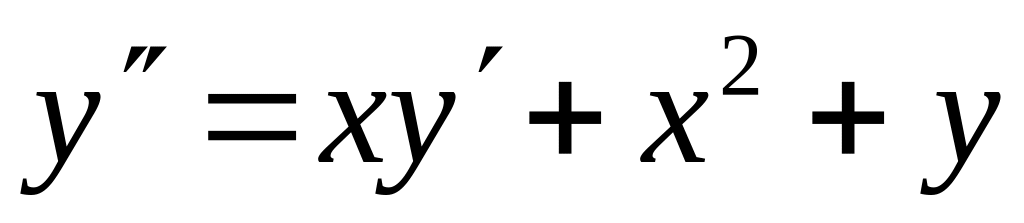.Разложить в ряд Фурье .
Вариант 24
Исследовать сходимость рядов 1)
,
2)
.
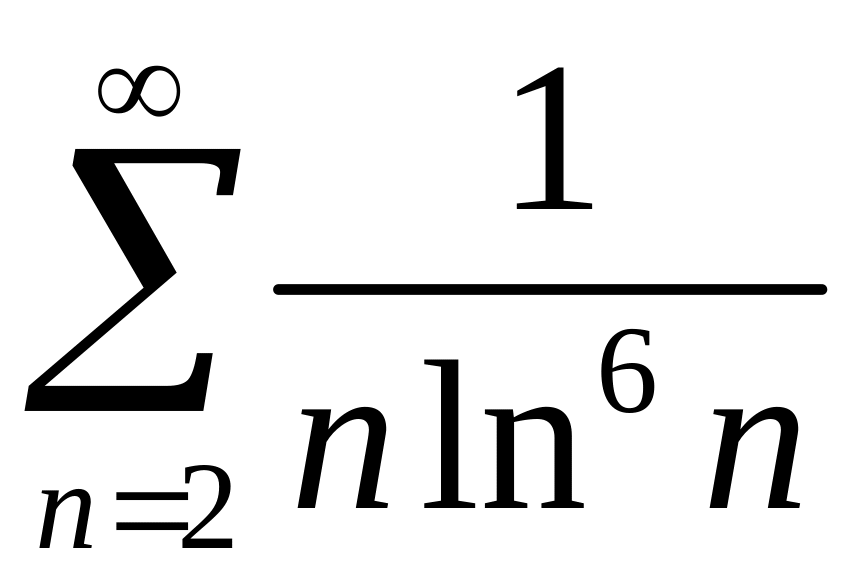Исследовать сходимость знакопеременных рядов
1)
,
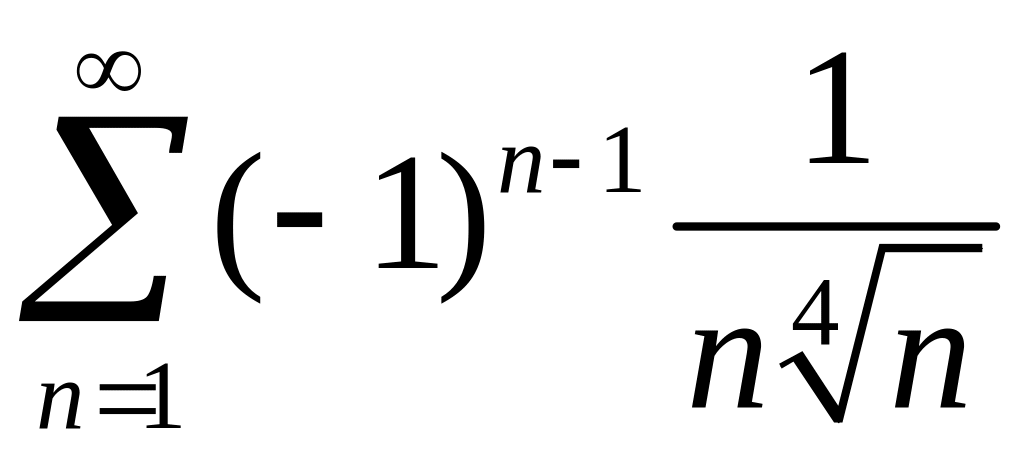2)
.
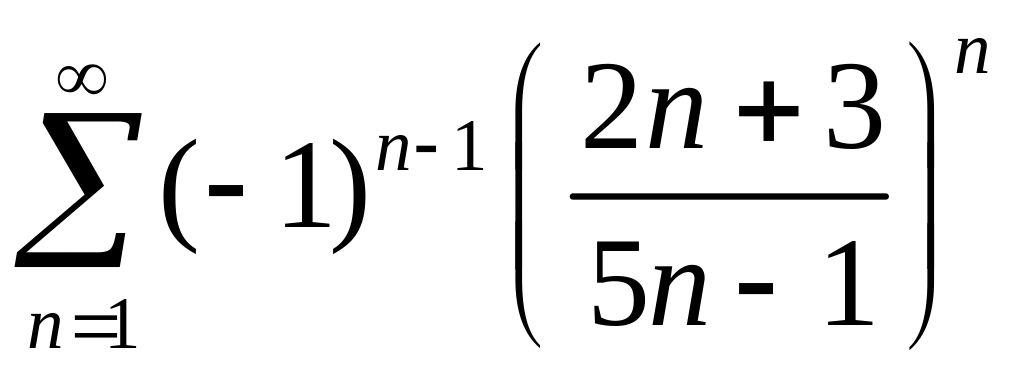Найти область сходимости степенного ряда .
Функцию
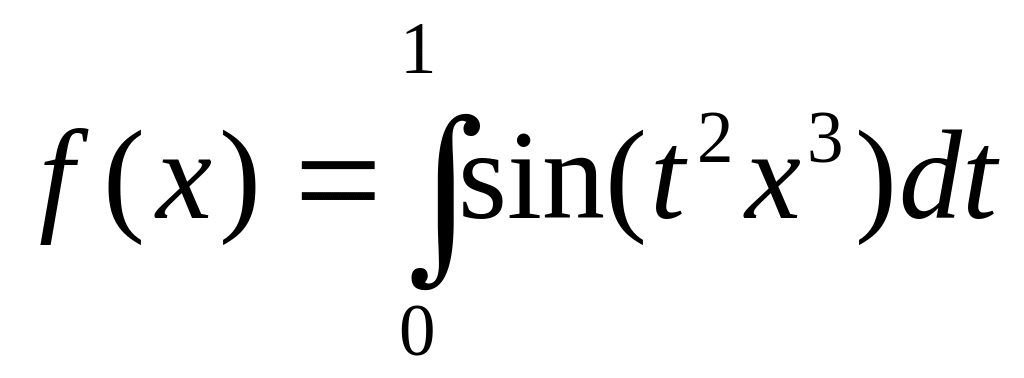разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
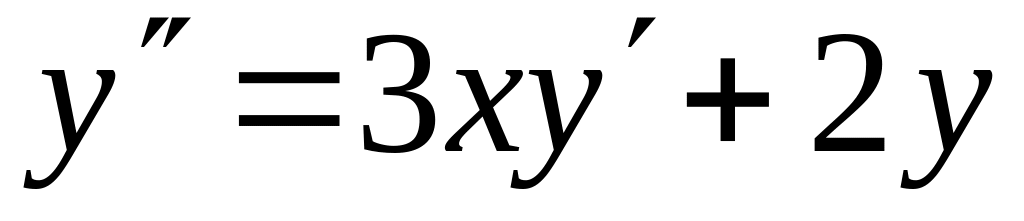.Разложить в ряд Фурье
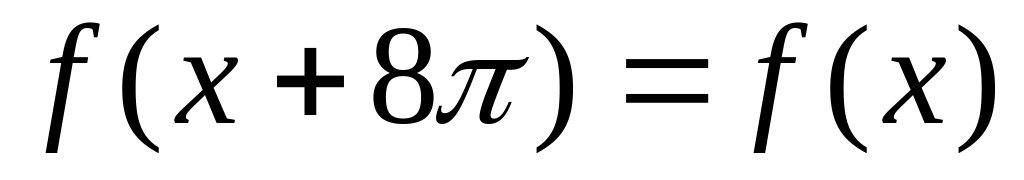
Вариант 25
Исследовать сходимость рядов 1)
,
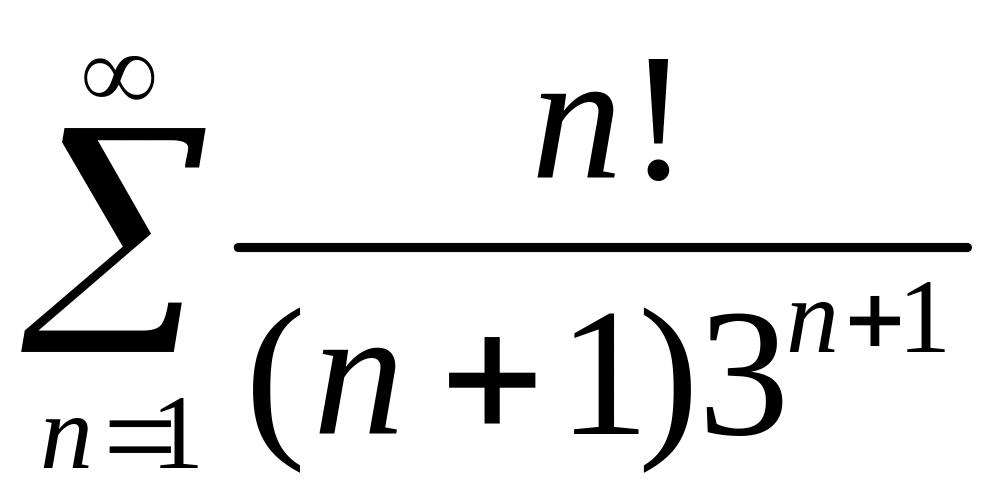2)
.
Исследовать сходимость знакопеременных рядов
1)
,
2)
.
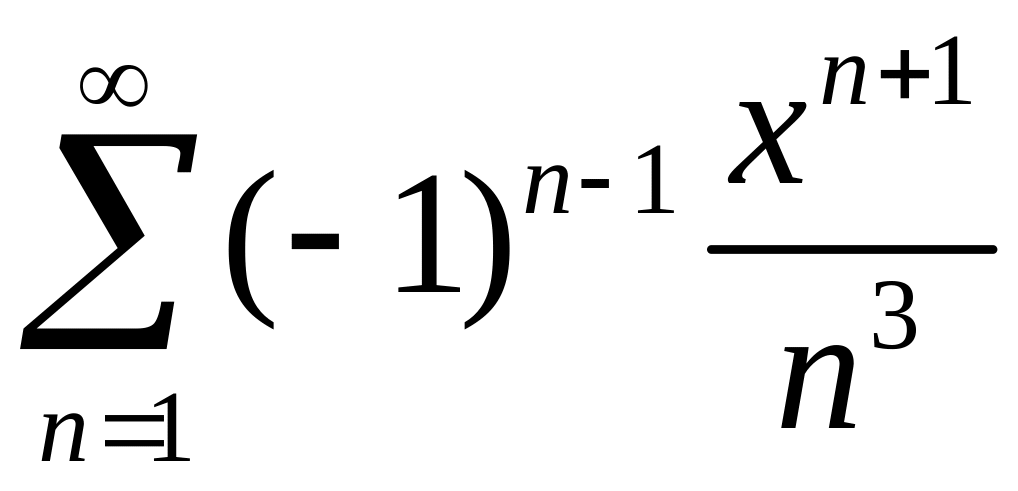.Функцию
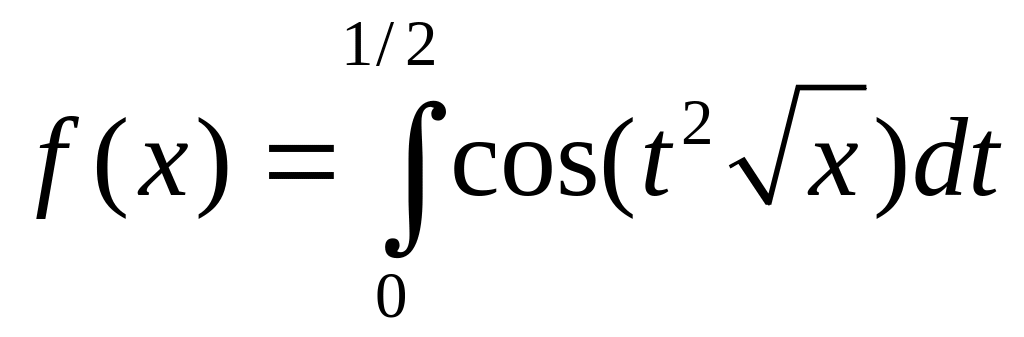разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
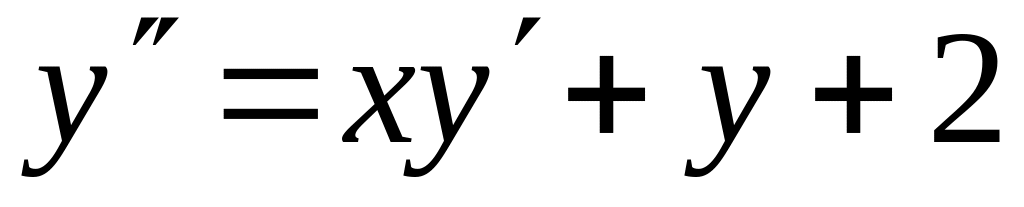.Разложить в ряд Фурье .
Вариант 26
Исследовать сходимость рядов 1)
,
2)
.
Исследовать сходимость знакопеременных рядов
1)
,
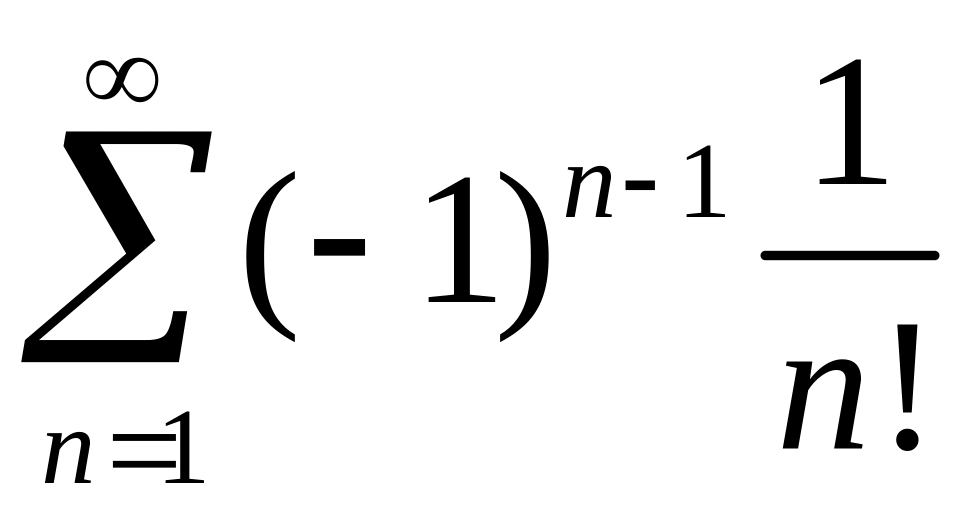2)
.
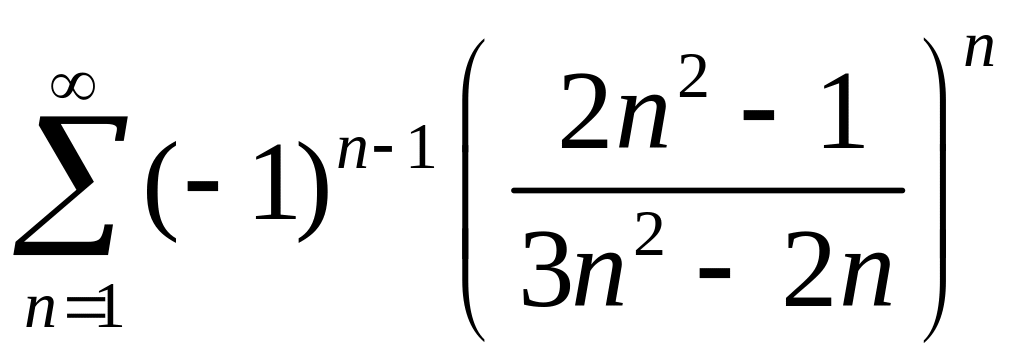Найти область сходимости степенного ряда .
Функцию разложить в ряд по степеням x. Пользуясь полученным разложением, вычислить с точностью 0,01.
Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
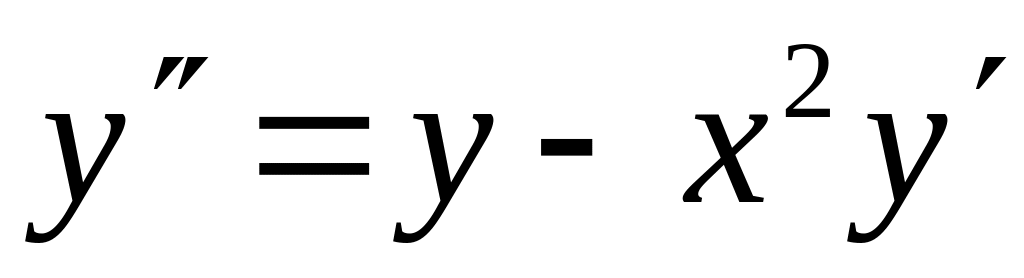.Разложить в ряд Фурье
.
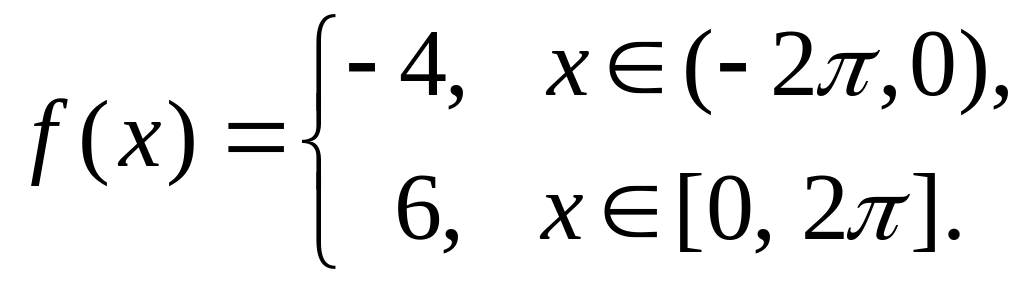Вариант 27
Исследовать сходимость рядов 1)
,
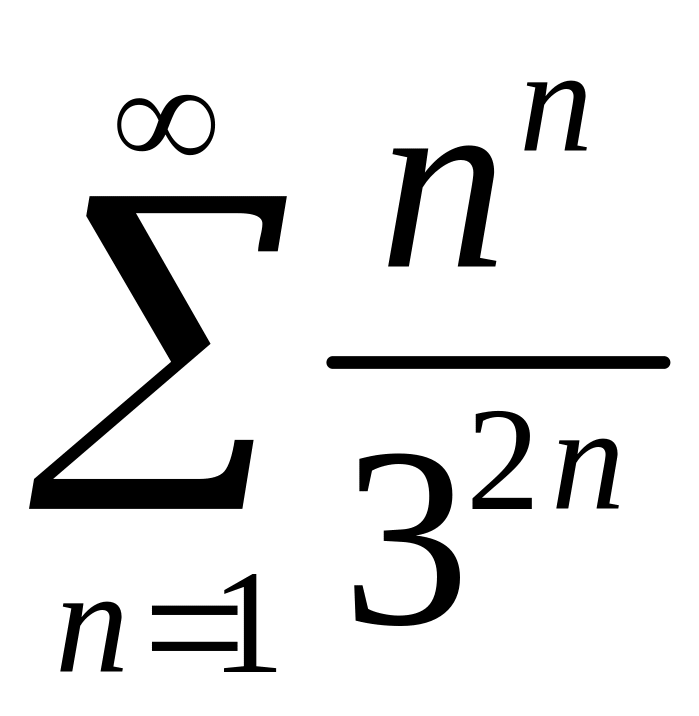2)
.
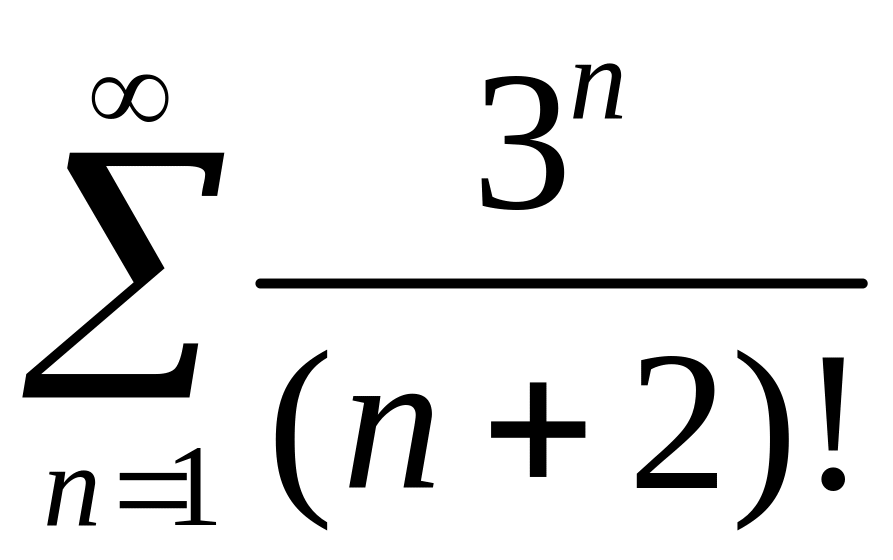Исследовать сходимость знакопеременных рядов
1)
,
2)
.
Найти область сходимости степенного ряда
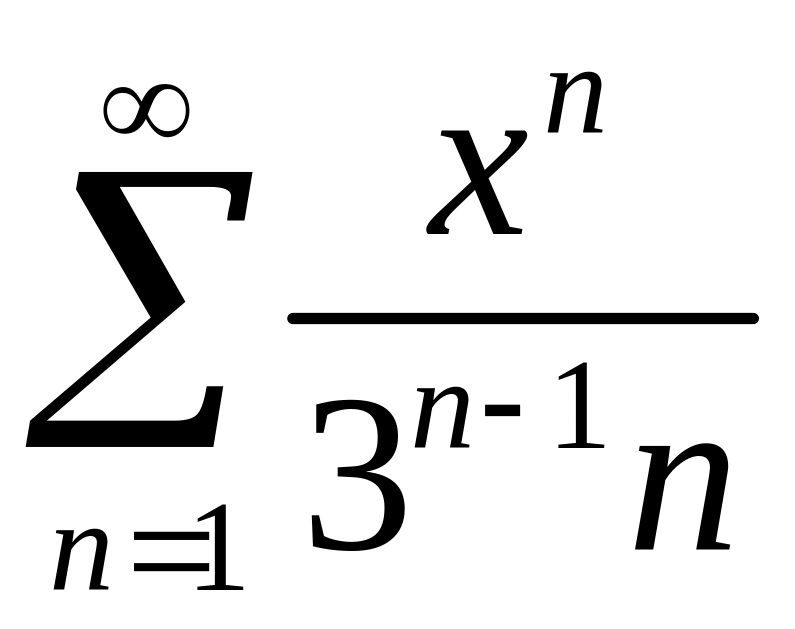.Функцию
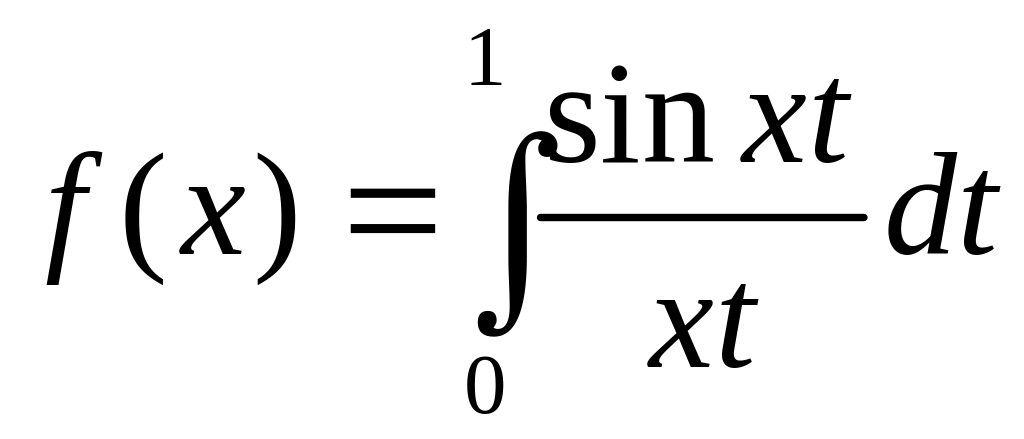разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
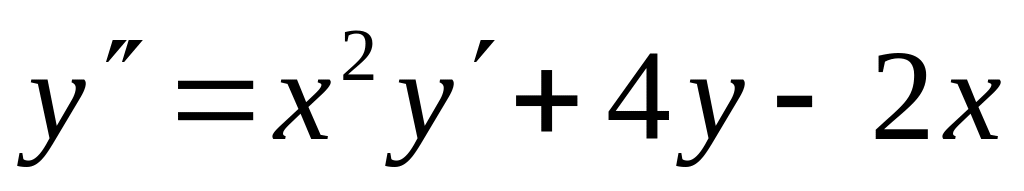.Разложить в ряд Фурье .
Вариант 28
Исследовать сходимость рядов 1)
,
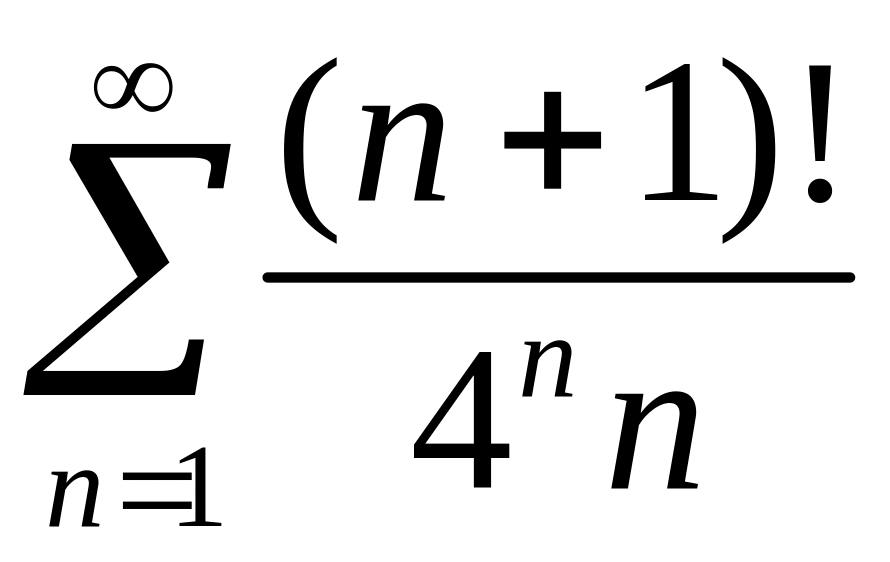2)
.
Исследовать сходимость знакопеременных рядов
1)
,
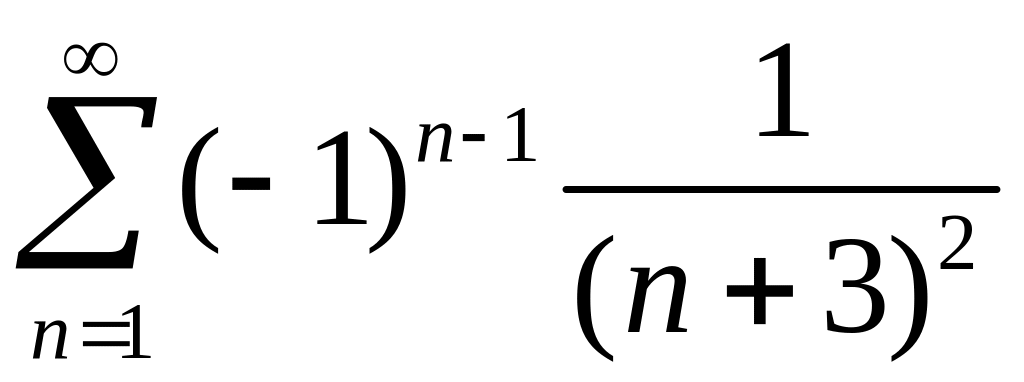2)
.
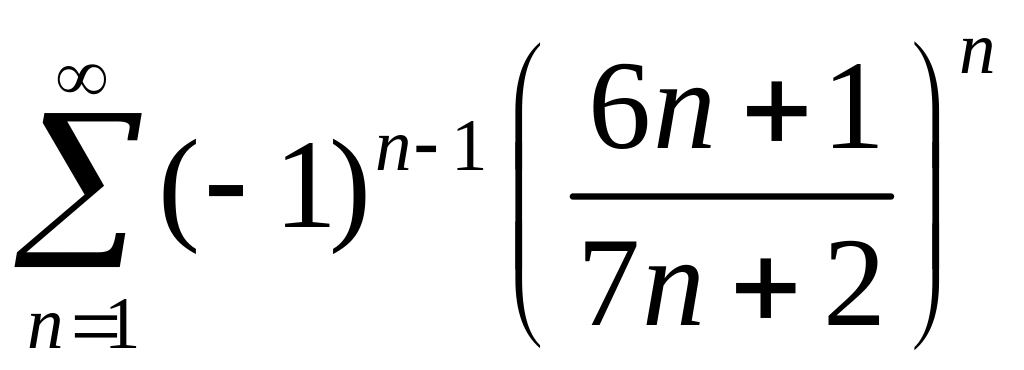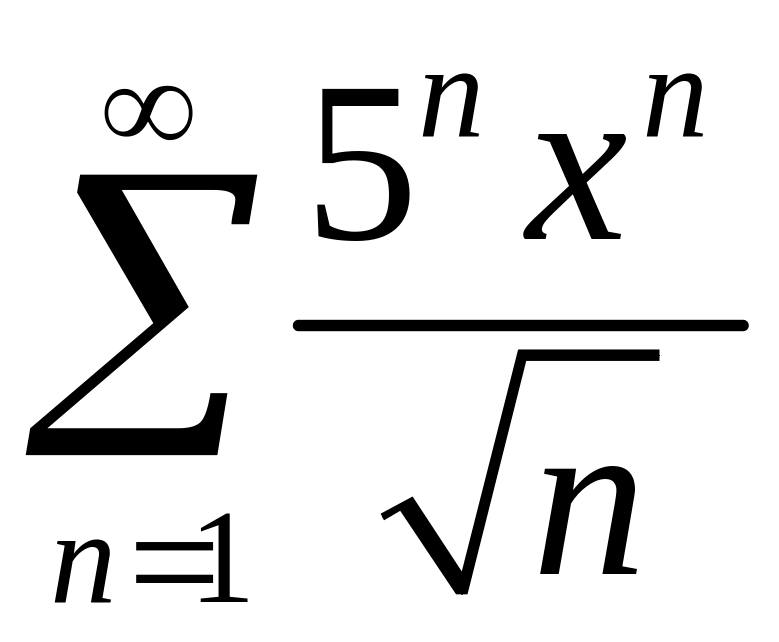.Функцию
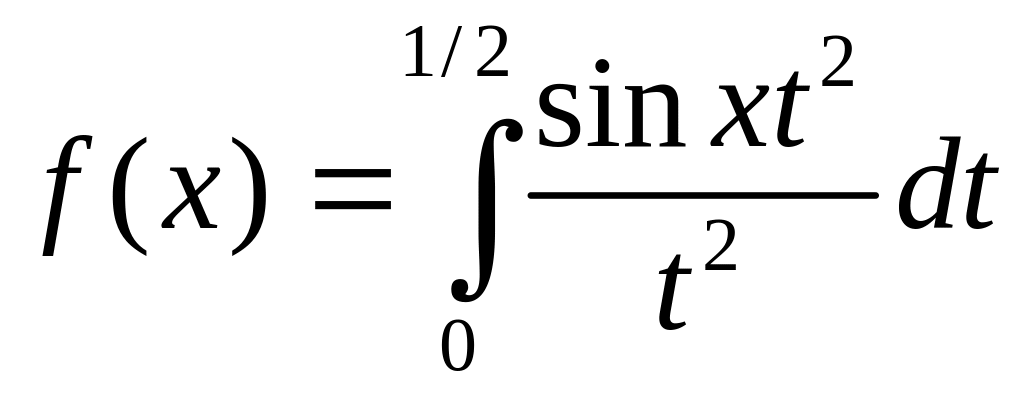разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
.Разложить в ряд Фурье .
Вариант 29
Исследовать сходимость рядов 1)
,
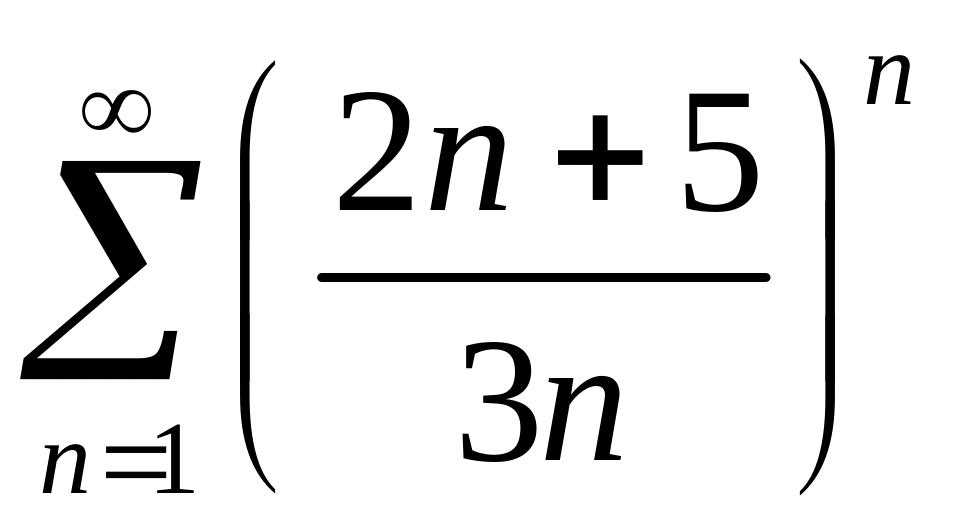2)
.
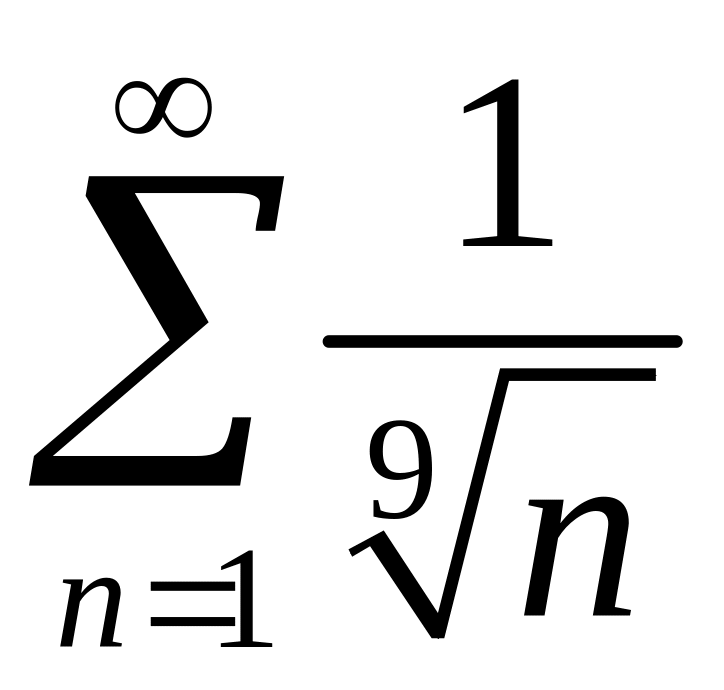Исследовать сходимость знакопеременных рядов
1)
,
2)
.
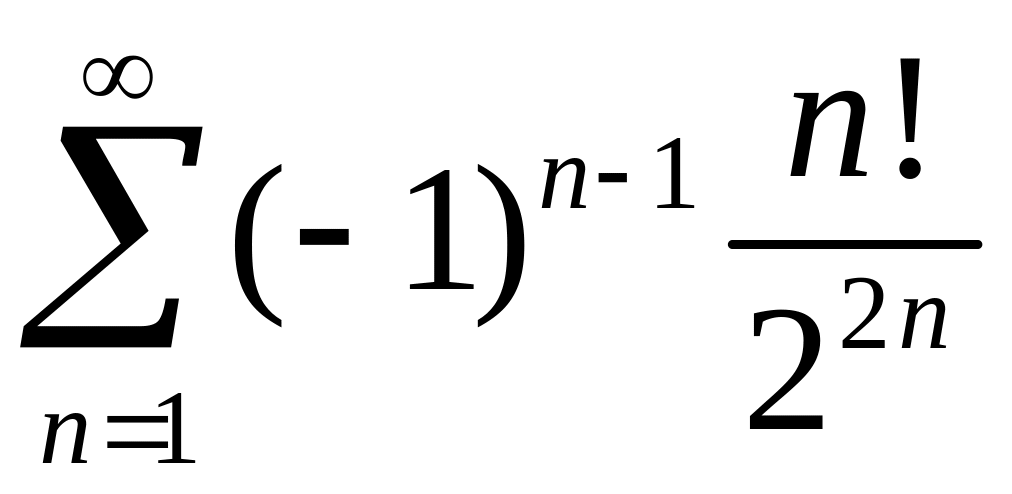Найти область сходимости степенного ряда
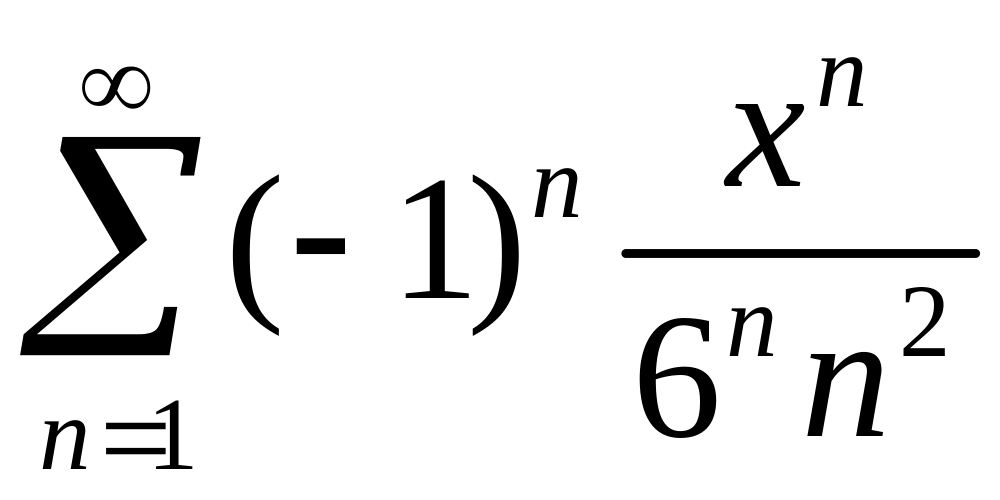.Функцию
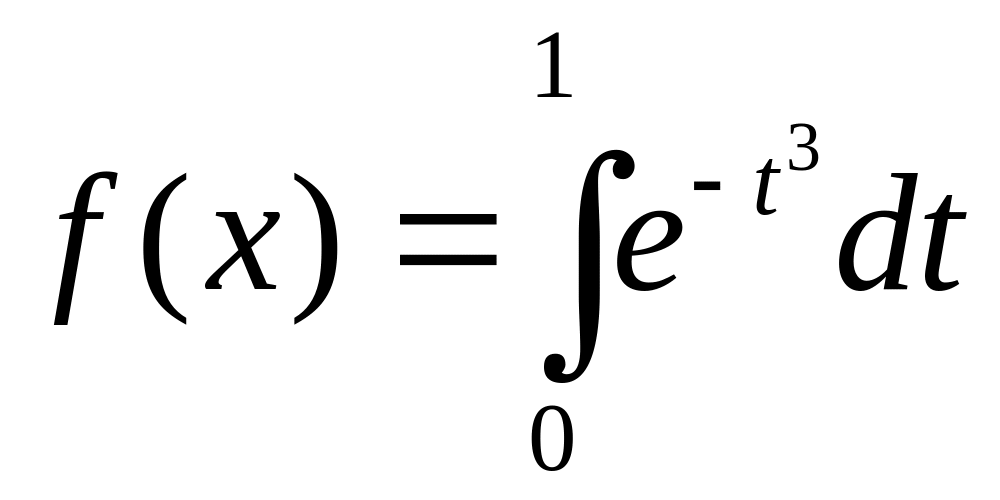разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения
,
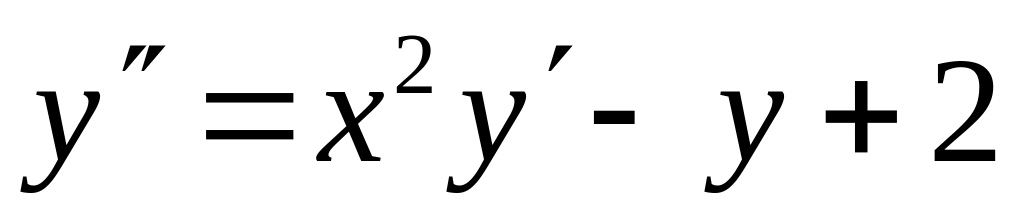.Разложить в ряд Фурье
.
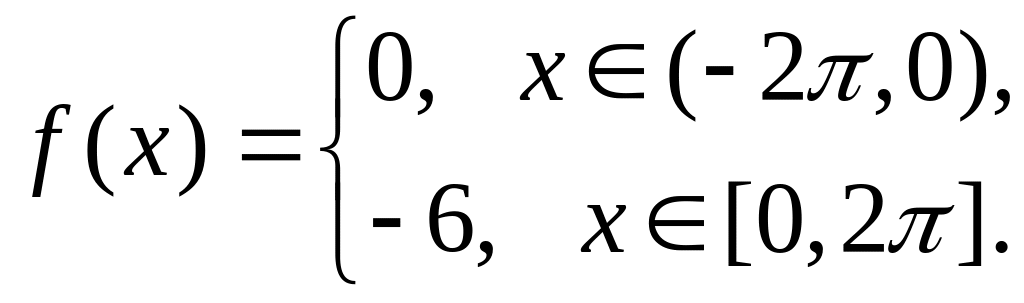Вариант 30
Исследовать сходимость рядов 1)
,
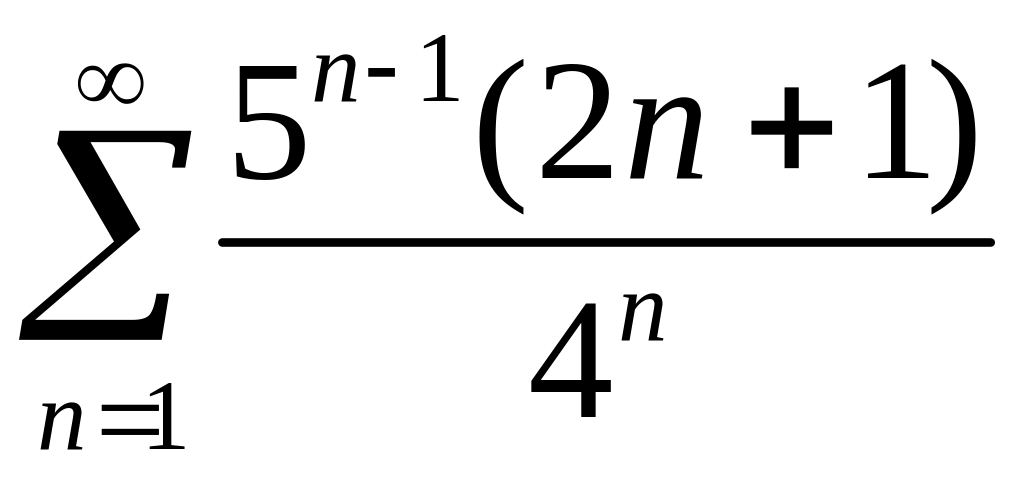2)
.
Исследовать сходимость знакопеременных рядов
1)
,
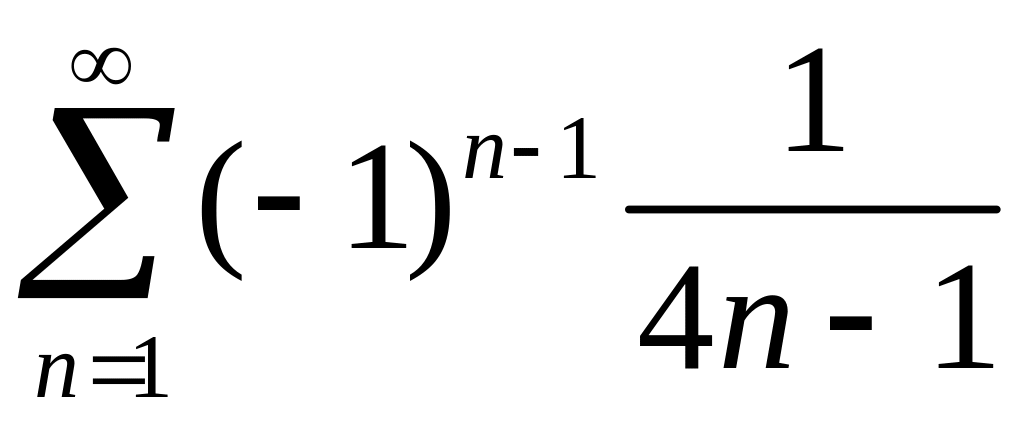2)
.
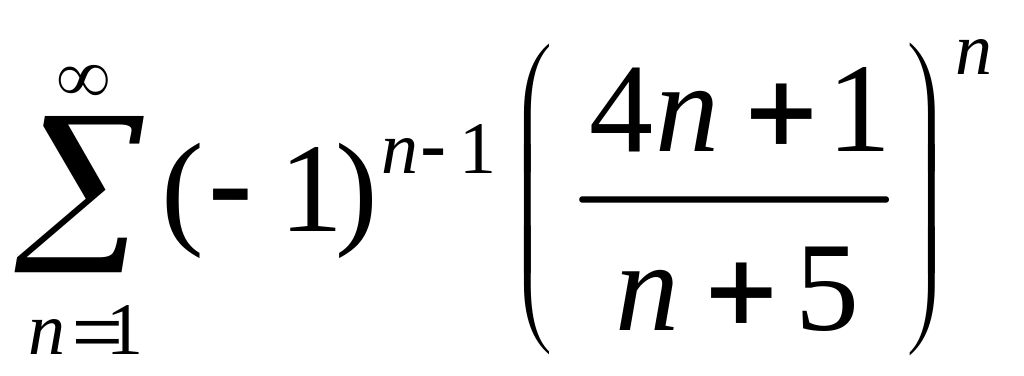Найти область сходимости степенного ряда
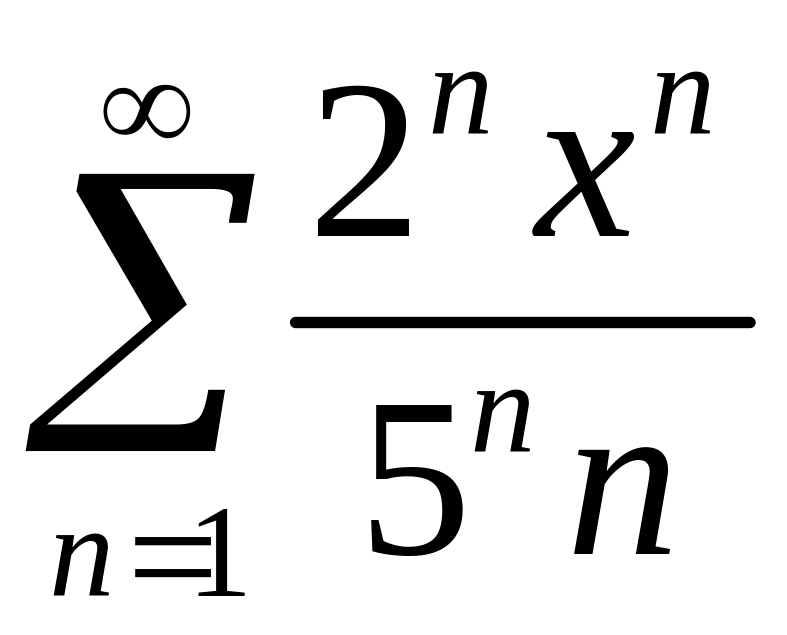.Функцию
разложить в ряд по степеням x.
Пользуясь полученным разложением,
вычислить
с точностью 0,01.Найти четыре члена разложения в ряд по степеням x решения дифференциального уравнения , .
Разложить в ряд Фурье .
1
Напомним,
что последовательность
называется
геометрической прогрессией со
знаменателем q,
если для любого n
отношение
.
2Напомним,
что
;
если конечный
предел в правой части этого равенства
существует, то несобственный интеграл
называется сходящимся, если не существует,
то расходящимся.
3
Здесь
(m-факториал)
– произведение всех натуральных чисел
от 1 до m.
4
При
ряд
состоит из нулей и признак Даламбера
применять нельзя, но ряд, конечно,
сходится.