3. Знакопеременные ряды. Абсолютная сходимость

1. Сведения из теории

Ряд

называется абсолютно сходящимся, если сходится ряд

,

составленный из абсолютных величин (модулей) его членов. Абсолютно сходящийся ряд сходится. Ряд называется условно (не абсолютно) сходящимся, если он сам сходится, но ряд из абсолютных величин его членов расходится.

Абсолютно сходящиеся ряды, в отличие от условно сходящихся рядов, аналогичны конечным суммам. Например, при перестановке местами членов абсолютно сходящегося ряда сумма ряда не меняется, а перестановкой местами членов условно сходящегося ряда можно получить ряд с любой суммой или даже расходящийся ряд.

Будем пользоваться следующими признаками сходимости знакопеременных рядов.

Признак Даламбера. Если существует то при ряд сходится абсолютно, а при расходится.

Корневой признак Коши. Если существует , то при ряд сходится абсолютно, а при расходится.

Достаточный признак расходимости. Если , то ряд расходится.

Признак Лейбница. Если для знакочередующегося ряда

последовательность убывает и стремится к нулю (это записывается обычно так: ), то ряд сходится, и его сумма .

2. Примеры решения задач

1. Исследовать на сходимость ряд .

◄ Применим признак Даламбера: , ,

.

Следовательно, ряд сходится абсолютно. ►

2. Исследовать на сходимость ряд .

◄ Применим корневой признак Коши:

, .

Следовательно, ряд сходится абсолютно. ►

3. Исследовать на сходимость ряд .

◄ Общий член ряда 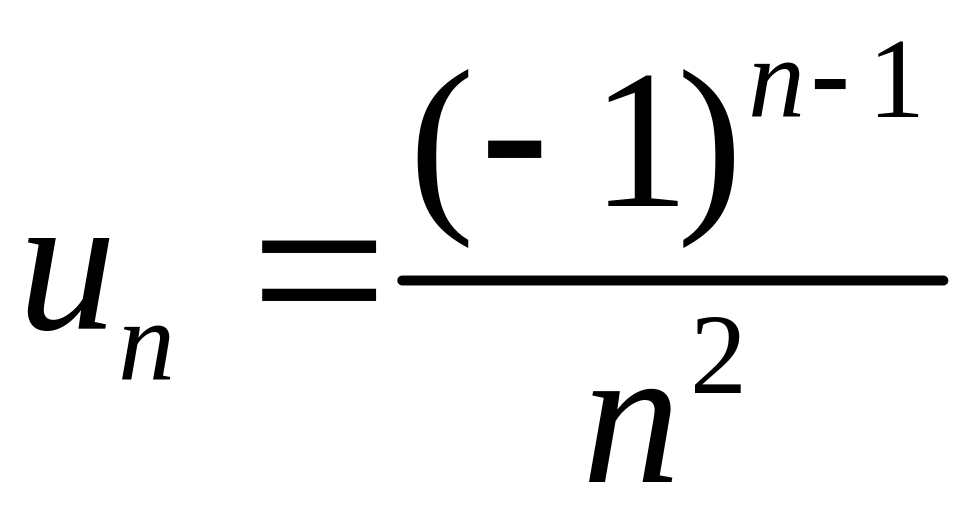. Его модуль (абсолютная величина) . Ряд исследован в примере 2.2.4 – он сходится. Но это означает, что ряд сходится абсолютно. ►

4. Исследовать на сходимость ряд

◄ Ряд знакочередующийся, последовательность (убывает и стремится к нулю). По признаку Лейбница ряд сходится. Ряд из абсолютных величин расходится согласно примеру 2.2.5. Поэтому ряд (3.3) сходится условно. ►

5. Исследовать на сходимость ряд .

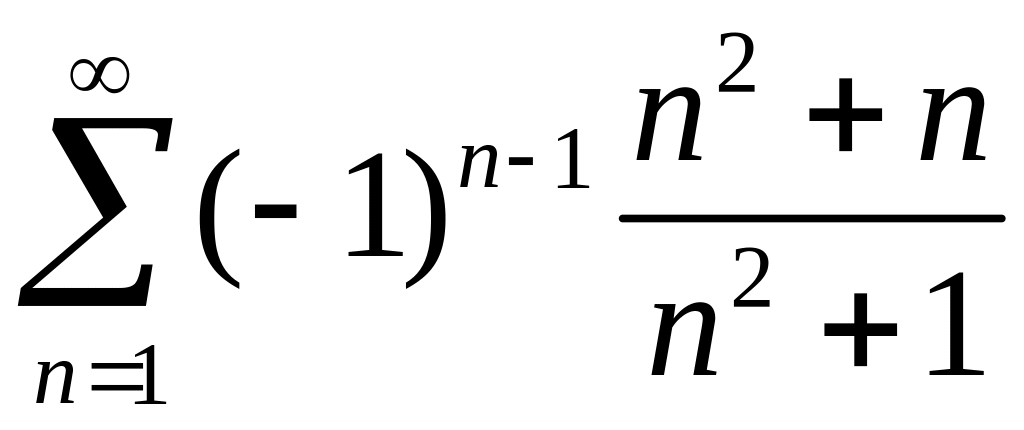◄ Так как , то из достаточного признака расходимости следует, что ряд расходится. ►

6. Доказать, что ряд сходится. Найти сумму ряда с точностью 0,01.

◄ Так как ряд знакочередующийся, а , то согласно признаку Лейбница ряд сходится. Представим сумму ряда в виде

По признаку Лейбница

.

Поэтому с точностью 0,01 сумма ряда . ►

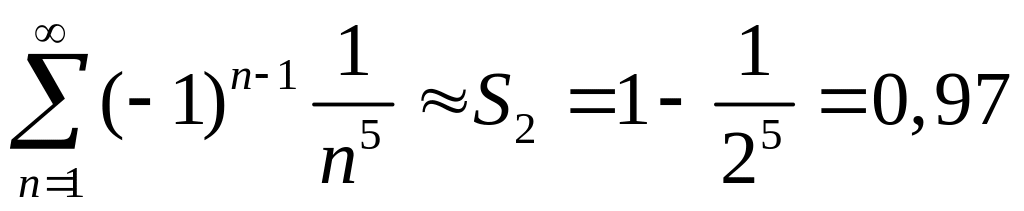3. Задачи для самостоятельного решения

Исследовать ряды на сходимость.

.	.
.	.
.	.

4. Функциональные ряды. Степенные ряды

1. Сведения из теории

Функциональным рядом называется формальное выражение вида

,

где – последовательность функций одной действительной переменной с общей областью определения D.

Областью сходимости функционального ряда называется множество тех точек , в которых сходится числовой ряд 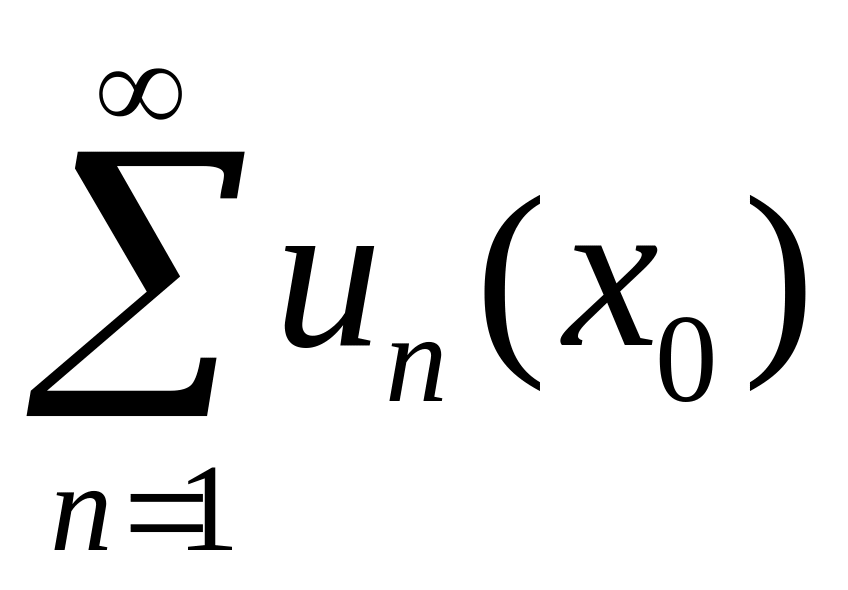. Суммой функционального ряда называется функция , , значением которой в каждой точке является сумма соответствующего числового ряда:

.

Степенным рядом называется функциональный ряд вида

Для любого степенного ряда существует такое R , что в интервале с центром в точке и радиусом R ряд сходится, а при – ряд расходится.

Интервал называется интервалом сходимости, а R – радиусом сходимости степенного ряда. На концах интервала сходимости ряд может как сходиться, так и расходиться.

Радиус сходимости можно найти по формуле

,

если этот предел существует.

Заметим, что эта формула получается применением к степенному ряду признака Даламбера. Поэтому при нахождении интервала сходимости конкретного степенного ряда можно либо пользоваться формулой , либо непосредственно применять признак Даламбера.
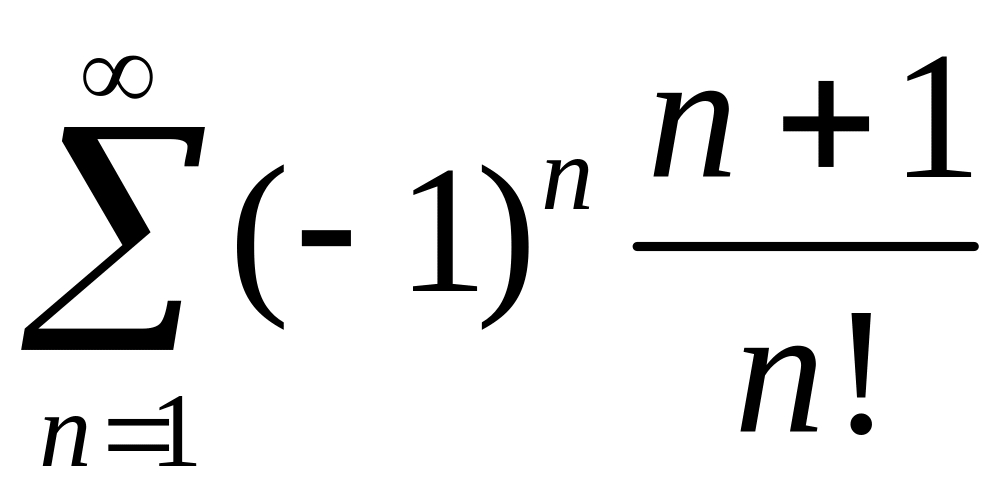