Министерство образования и науки РФ

Государственное образовательное учреждение

высшего профессионального образования

«Ярославский государственный технический университет»

2986

Р Я Д Ы

Ярославль

2011

Министерство образования и науки РФ

Государственное образовательное учреждение

высшего профессионального образования

«Ярославский государственный технический университет»

Кафедра «Высшая математика»

Рекомендовано советом

инженерно-экономического

факультета

Р Я Д Ы

Методические указания

Ярославль 2011

УДК 517(07)

МУ 97-10. Ряды: метод. указания / сост. : В. Ш. Ройтенберг, Л. А. Сидорова. – 2-е изд., изм. и доп. – Ярославль : Изд-во ЯГТУ, 2011. – 40 с.

Содержат краткие теоретические сведения по разделу «Ряды», подробно разобранные типовые задачи. Даны задачи для самостоятельного решения, 30 вариантов контрольной работы. Методические указания составлены для использования студентами при выполнении контрольной работы и подготовке к экзамену.

Предназначены для студентов всех специальностей ФДПО.

Библиогр. 2.

Рецензенты: кафедра высшей математики Ярославского государственного технического университета;

Л. Б. Медведева, канд. физ.-мат. наук, доцент кафедры общей математики ЯрГУ им. Демидова.

_____________________________________________________________

Редактор л.С. Кокина План 2010

Подписано в печать 7.06.2011. Формат 60х84 1/16. Бумага белая.

Печать ризограф. Усл. печ. л. 2,32. Уч.-изд. л. 2,30.

Тираж 275. Заказ

Ярославский государственный технический университет

150023, Ярославль, Московский пр., 88

Типография Ярославского государственного технического университета

150000, Ярославль, ул. Советская, 14а

_____________________________________________________________

 Ярославский государственный технический университет, 2011

1. Понятие сходимости ряда. Сумма ряда

1. Сведения из теории

Числовым рядом называется формальное выражение вида

,

где , … – числовая последовательность. Числа называются членами ряда. Конечная сумма называется n-й частичной суммой ряда. Если существует конечный предел последовательности частичных сумм , то ряд называется сходящимся, а число S – суммой ряда, при этом пишут . Ряд, не являющийся сходящимся, называется расходящимся.

Равенство означает, что для любого числа найдется номер такой, что при . Поэтому частичные суммы с номерами являются приближенным значением суммы ряда S с точностью ε.

Необходимый признак сходимости ряда. Если ряд сходится, то .

Следствие (Достаточный признак расходимости ряда). Если , то ряд расходится.

2. Примеры решения задач

1. Исследовать сходимость геометрического ряда

,

члены которого образуют геометрическую прогрессию¹ со знаменателем q.

◄ Сходимость ряда означает существование конечного предела S последовательности частичных сумм ряда

, , …

Умножим на q:

.

Тогда , , .

Если , то есть , то и потому .

Если , то , а потому и .

Если , то и .

Если , то при четных n и при нечетных n. Поэтому не существует.

Таким образом,

при геометрический ряд сходится и его сумма ,

при геометрический ряд расходится. ►

2. Убедиться, что ряд сходится, и найти его сумму.

◄ Ряд можно переписать в виде 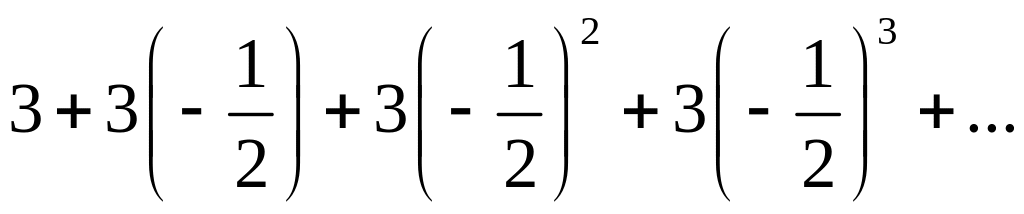, то есть он представляет собой геометрический ряд со знаменателем . Так как , то ряд сходится, и его сумма . ►

3. Исследовать сходимость ряда .

◄ = . Согласно достаточному признаку расходимости – ряд расходится. ►

3. Задачи для самостоятельного решения

Убедиться в сходимости следующих рядов и найти их суммы.

Доказать расходимость рядов, используя достаточный признак расходимости.

.

.

2. РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ

1. Сведения из теории

1. Признаки сходимости рядов с положительными членами

1. Признак Даламбера. Если для ряда существует то при 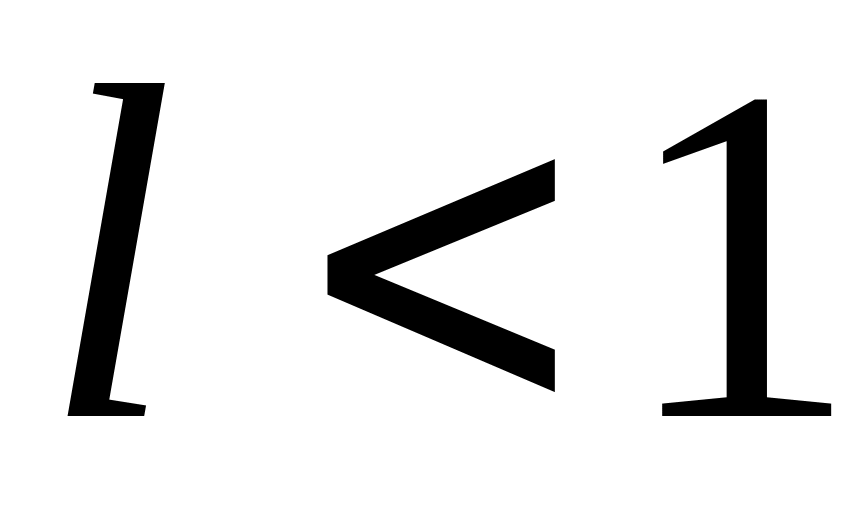ряд сходится, а при ряд расходится.

Суть признака Даламбера состоит в том, что при достаточно больших n , то есть члены ряда ведут себя примерно как члены геометрического ряда со знаменателем l, который сходится при и расходится при .

2. Корневой признак Коши. Если для ряда существует 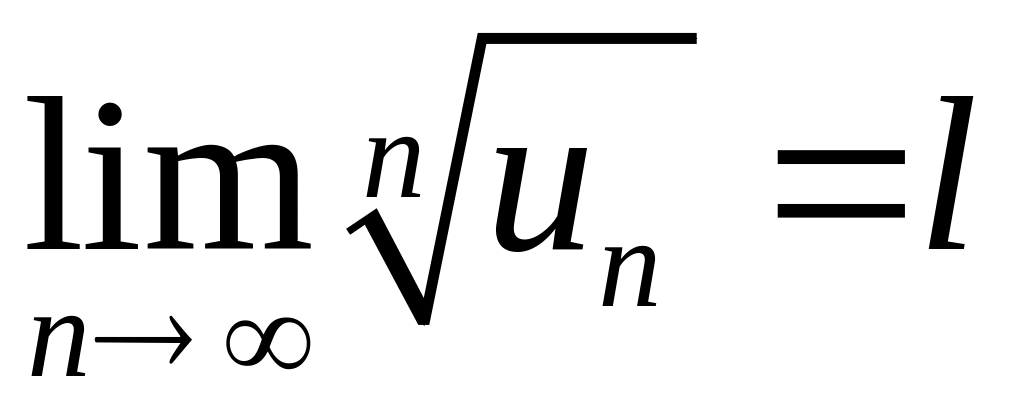, то при ряд сходится, а при ряд расходится.

Суть признака Коши состоит в том, что при достаточно больших n , то есть члены ряда ведут себя примерно как члены геометрического ряда со знаменателем l, который сходится при и расходится при .

3. Интегральный признак Коши. Если 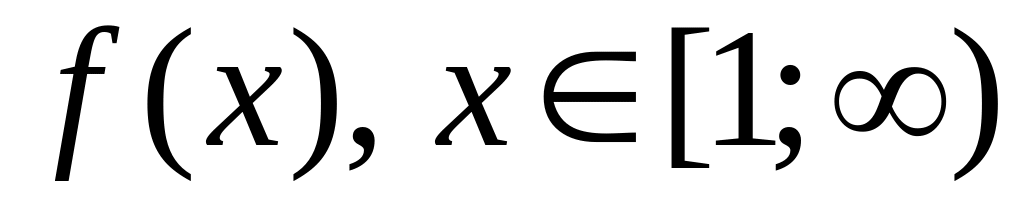– непрерывная положительная убывающая функция, то из сходимости (расходимости) несобственного интеграла² следует сходимость (расходимость) ряда , где .

Интегральный признак – более «тонкий» признак, чем признак Даламбера и корневой признак, и обычно применяется в случаях, когда , , то есть когда признак Даламбера и корневой признак не действуют.