Свойства кривой Безье

• непрерывность заполнения сегмента между начальной и конечной точками;

• кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные точки;

• при наличии только двух контрольных точек сегмент представляет собой прямую линию;

• прямая линия образуется при коллинеарном (на одной прямой) размещении управляющих точек;

• кривая Безье симметрична, то есть обмен местами между начальной и конечной точками (изменение направления траектории) не влияет на форму кривой;

• масштабирование и изменение пропорций кривой Безье не нарушает ее стабильности, так как она с математической точки зрения «аффинно инвариантна»;

• изменение координат хотя бы одной из точек ведет к изменению формы всей кривой Безье;

• степень кривой всегда на одну ступень ниже числа контрольных точек. Например, при трех контрольных точках форма кривой — парабола;

• окружность не может быть описана параметрическим уравнением кривой Безье;

• невозможно создать параллельные кривые Безье, за исключением тривиальных случаев (прямые линии и совпадающие кривые).

Применение в компьютерной графике

Благодаря простоте задания и манипуляции, кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки опорных точек, то не пересекаются и сами кривые), а с другой стороны позволяет осуществлять интуитивно понятное управление параметрами кривой в графическом интерфейсе с помощью её опорных точек. Кроме того аффинные преобразования кривой (перенос, масштабирование, вращение и др.) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.

Наибольшее значение имеют кривые Безье второй и третьей степеней (квадратичные и кубические). Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. В программах векторной графики наподобие Adobe Illustrator или Inkscape подобные фрагменты известны под названием «путей» (path).

Апроксимація функцій Методом найменших квадратів.

При інтерполюванні основною умовою є проходження графіка інтерполяційного многочлена через дані значення функції у вузлах інтерполяції. Однак виконання цієї умови в деяких випадках є недоцільним. Наприклад, при великому числі вузлів інтерполяцї одержуємо високу степінь полінома у випадку глобальної інтерполяції (це пов’язано з рядом неприємностей – осциляція функції). Крім того, табличні дані можуть містити в собі похибки вимірювань. Отже, інтерполюючий многочлен теж повторював би ці похибки. Вихід із цього становища може бути знайдений вибором такої функції φ(х), графік якої якнайближче проходить від даних точок (х_і, у_і).

Поняття “близько” уточнюється при розгляді окремих видів наближення.

Середньо-квадратичне наближення. Мірою відхилення інтерп. функції φ(х) від заданої f(х) на множині точок (x_i, y_i) (і = ) є величина, яка дорівнює сумі квадратів різниць між значеннями многочлена та функції в даних точках

Цей вираз називається сумарною квадратичною похибкою. Очевидно що буде середньою квадратичною похибкою

При побудові апроксимуючого ф-ї (тут як правило )потрібно підібрати коефіцієнти а₀, а₁, … , а_m так, щоб величина була мінімальна. В цьому полягає ідея методу найменших квадратів.

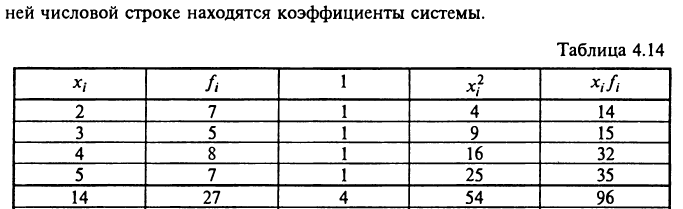
Наприклад якщо то отримаємо самий простий випадок

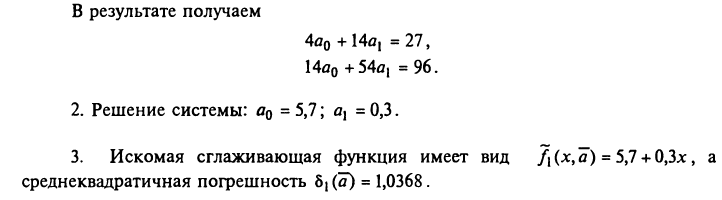
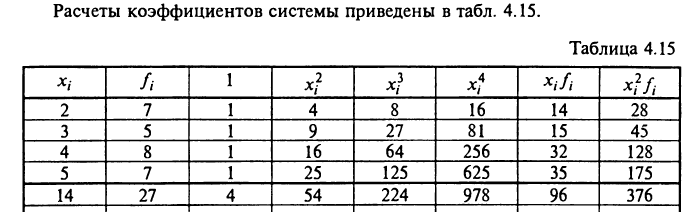
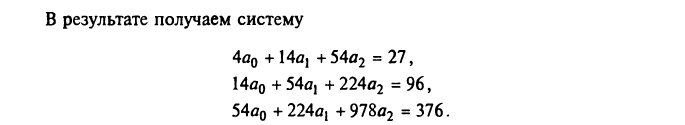
Розв’язавши систему отримаємо , ,

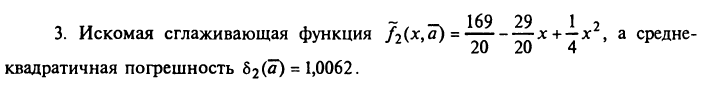
Просторова інтерполяція. побудова цифрових моделей рельєфу

Уметеорології інтерполюються дані спостережень метеостанціи для одержання карт погоди на великі території, інтерполюються дані океанологічних і гідрологічних вимірювань, будуються поля кон-центрацій речовин у різних середовищах та ін. У геології інтерполяція застосовується для побудови двовимірних і тривимірнихмоделей підземних масивів за даними точкових шпар.Для створення інтерпольованої карти необхідний набір точок з даними про їх просторове положення (координати х,у в деякій системі к-т або у вигляді широти/довготи) і кількісне значення параметра ( ) у цих точках - висота, тиск,температура, концентрація забруднювача та ін.

Завданням просторової інтерполяції є побудова суцільної поверхні з заданим розміром кроку сітки вузлів, на основі мережі вихідних точок. Залежно від необхідної просторової точності вибирається різний крок (наприклад, ділянка розміром 10x10 км може бути інтерпольована із кроком 100 м (100x100 вузлів сітки) або з кроком 10 м (1000x1000 вузлів)

У більшості практичних випадків мережа таких вихідних точок нерегулярна, має різну щільність, великі розриви тощо.

Методи просторової інтерполяції використовують поліноми різних ступенів вигляду

(8-1)

де - коефіцієнти полінома; - порядок полінома.

Перші чотири рівняння (8.1), тобто поліноми нульового, першого, другого і третього ступеня, є:

- горизонтальна площина:

- похила площина:

- квадратична поверхня:

- кубічна поверхня:

Таким чином, горизонтальнаповерхня має порядок нуль, похила плоска поверхня - перший

порядок, квадратична поверхня -другий порядок,

кубічна поверхня з десятьма коефіцієнтами має третій порядок.

Знаходження коефіцієнтів є стандартною процедурою в

задачах інтерполяції, тому обчислення легко виконуються за

допомогою стандартних статистичних пакетів.

Т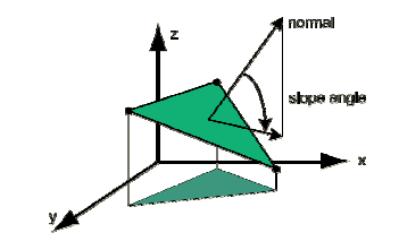 ріангуляційна модель або TIN-модель (Triangulated Irregular Network – нерегулярна тріангуляційна мережа) являє собою систему трикутників, яка побудована на нерегулярній множині точок, що не перекривають один одного. Вершинами трикутників є первинні опорні точки. У цьому випадку, рельєф є багатогранною поверхнею, кожна грань якої описується або лінійною функцією, або поліномінальною поверхнею, коефіцієнти якої визначаються за значеннями у вершинах граней трикутників. Будь-який набір точок, за винятком деяких простих випадків, допускає два або більше способів тріангуляції. Для отримання моделі поверхні, ГІС з'єднує пари точок ребрами певним способом, названим тріангуляцією Делоне. За визначенням Делоне три точки формують трикутник в тріангуляції тоді і тільки тоді, коли в колі, описаному довкола цього трикутника немає інших точок розбиття. Кожен круг, що обмежує трикутник, не містить точок з набору усередині нього.

Функція визначення висоти будується в кожній грані,

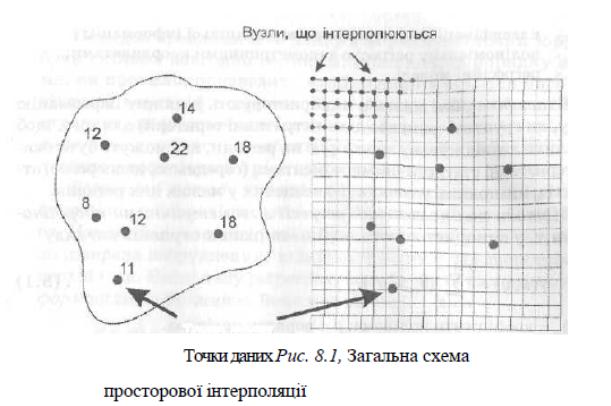
Просторове положення елемента TIN

У TIN-модели просторове положення трикутника характеризує

нормаль до його грані. Трикутник задається трьома точками

A(х1, у1, z1) B(x2, y2, z2) C(x3, y3, z3). Нормаль до площини трикутника

визначається нормальним вектором який виходить

в результаті векторного добутку векторів – двох сторін трикутника . Для нормального вектора кожного трикутника обчислюються:

1) прямокутні декартові координати:

2) направляючі косинуси: (косинуси кутів між нормаллю та осями к-т)

, , (Рис)

3) кути проекції у горизонтальній площині: , (Рис)

Ці залежності є базовими для вирішення завдань відображення і аналізу поверхні.

Експозиція схилу

Експозиція окремої грані визначається кутом між напрямом проекції нормалі на горизонтальну поверхню та напряму на Північ ( )

Тобто, экспозиция равна азимуту проекции нормали склона на горизонтальную плоскость

К ут обчислюють за формулою

Крутість грані

Крутість грані (нахил) визначається кутом нахилу нормалі до горизонтальної

площини. Він визначається як доповнення до 90 кута , тобто

де .

на основе рассчитанных для каждого треугольника угла

наклона и экспозиции склона в триангуляционных сетях

осуществляется анализ стоку атм. опадів.

Діапазони висот

В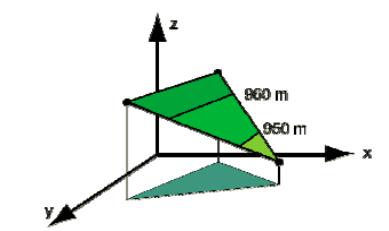 исота довільної точки всередині трикутника визначається за рівнянням

площини, заданої вершинами трикутника. Площина з нормальним

вектором , що проходить через точку A(х1, у1, z1)

описується рівнянням nx ( x – x1) + ny ( y – y1) + nz ( z – z1) = 0

Звідси по відомих значеннях x і y знаходяться висоти довільних точок. По кожній грані тріангуляції виконують Інтерполяцію ізоліній. Для цього досить знайти лінію перетину трикутника із площиною . Тобто підставивши у рівняння площини отримаємо nx ( x – x1) + ny ( y – y1) + nz ( z0 – z1) = 0 рівняння прямого відрізка у горизонтальній площині.

Отримана таким чином множина відрізків буде наближати ізолінію для заданого значення ламаною лінією – полігоном. Для згладження результатів потрібно застосовувати сплайн-інтерполяцію.

25