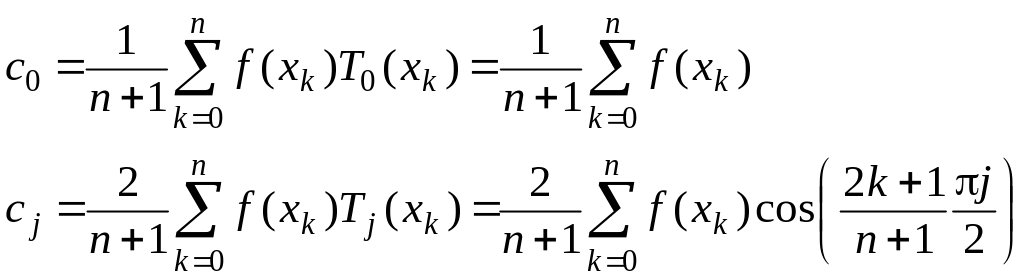Многочлени Чебишева

Якщо задана деяка функція на відрізку , то виникає питання: як обрати вузли інтерполяції так, щоб похибка наближення функції інтерполяційним многочленом була мінімальною. Виявляється, що мінімізувати величину похибки можна, якщо за вузли інтерполяції взяти корені поліномів Чебишева. Для простоти розглянемо відрізок зміни аргументу . Поліном Чебишева у цьому випадку задається формулою:

_, (0)

Покажемо, що для будь-якого натурального числа вираз (7) справді буде поліномом степеня .

Наприклад, при _, , при . Для більших використаємо тригонометричну формулу суми косинусів тоді

.

Покладемо . Тоді для полінома Чебишева можна записати:

,

або (0)

Ми отримали рекурентну формулу для поліномів Чебишева. Знаючи, що , і поширюючи рекурентну формулу на всю вісь , знайдемо:

.

.

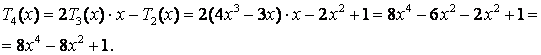і т.д.

Властивості поліномів Чебишева:

Властивість 1. При парному (непарному) поліном містить лише парні (непарні) степені , тобто є парною (непарною) функцією.

Властивість 2. Старший коефіцієнт полінома при дорівнює .

Властивість 3. Поліном має дійсних коренів на відрізку , які виражаються формулою: . (груп до країв рис!!!)

Д ійсно, .

Властивість 4. , причому , де , . (очевидно, оскільки по суті )

Дійсно, , , але тільки для .

Властивість 5. На границах отрезка значения многочленов Чебышева равны:

для парних , для парних (тобто досягають максим. знач.)

Теорема Чебышева (без дов). Среди всех многочленов степени , со старшим коэффициентом a_n равным единице, наименьшее уклонение от нуля, равное 1/2^n-1, имеет нормированный полином Чебышева .

Вузли, що мінімізують похибку інтерполяції

Візьмемо на відрізку в якості вузлів інтерполяції корені полінома Чебишева , тобто точки:

, .

Т оді багаточлен можна записати у такому вигляді:

(де , коренів многочлена )

і він буде пропорційним багаточлену Чебишева . Множник з’явився тому, що старший коефіцієнт багаточлена дорівнює одиниці, а старший коефіцієнт багаточлена , згідно властивості 2, дорівнює .

Таким чином, максимальна похибка інтерполяції за аналогією з многочленом Тейлора буде

,

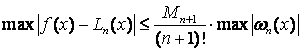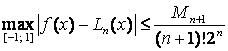
де _, , а згідно властивості 4 . Доведено, що ця похибка є мінімальною, а вузли інтерполяції є оптимальними для оцінки похибки на відрізку .

У випадку інтерполяції на довільному відрізку цей відрізок можна перевести у відрізок шляхом лінійної заміни змінних:

. Тоді .

При цьому кореням багаточлена Чебишева відповідатимуть точки:

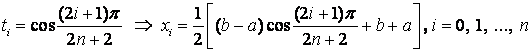. (19)

Приклад. Побудувати на проміжку [0,1] многочлен Чебишева четвертого степеня з коефіцієнтом 1 при старшому степені. Обчислити відхилення його від 0.

Розв’язання. У многочлені Чебишева

(див. попередню задачу) зробимо заміну змінної

.

При a=0, b=1 маємо =2x-1. Тоді многочлен Чебишева для проміжку [0,1] має вигляд

.

Шуканий нормований многочлен такий

.

Його відхилення від 0 дорівнює

.

Многочлени Чебишева широко використовуються при апроксимації функцій. Наближаючий поліном Чебишева P_n(x) степені <n для функції f(x) на інтервалі [-1;1] можна записати як суму поліномів {T_j(x)}:

Коефіцієнти {c_j} обчислюють за формулами