3. Результаты

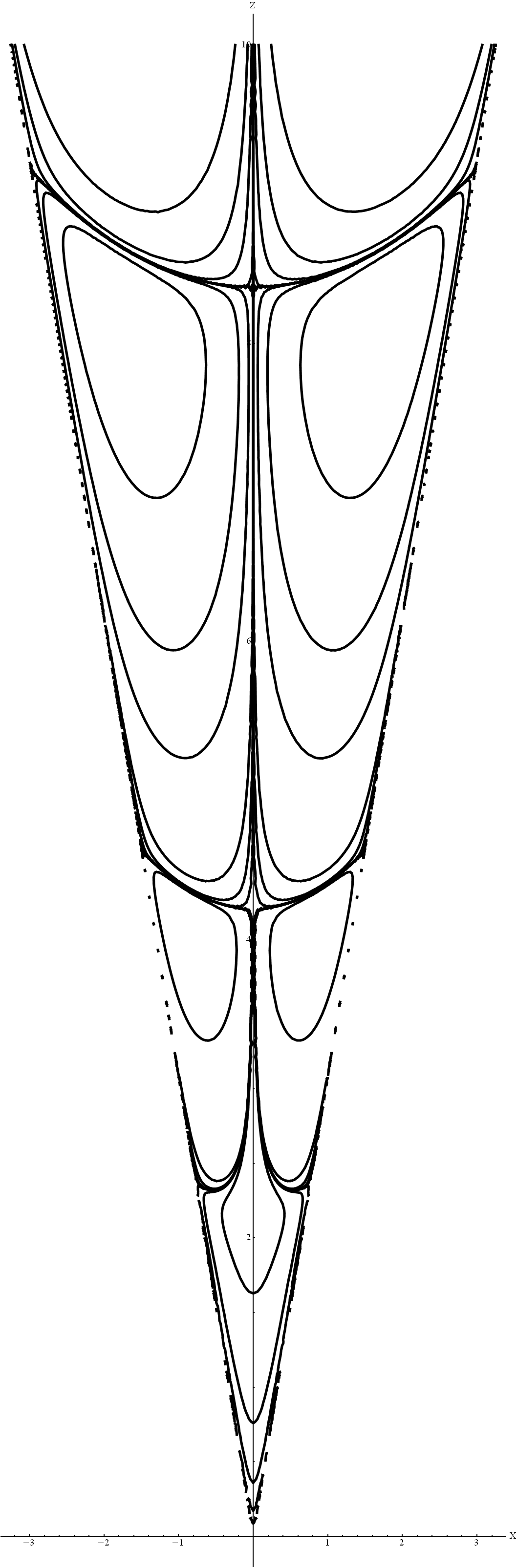
Рис. 3. Линии тока под воздействием стокслета, находящегося в точке в конусе с углом раствора

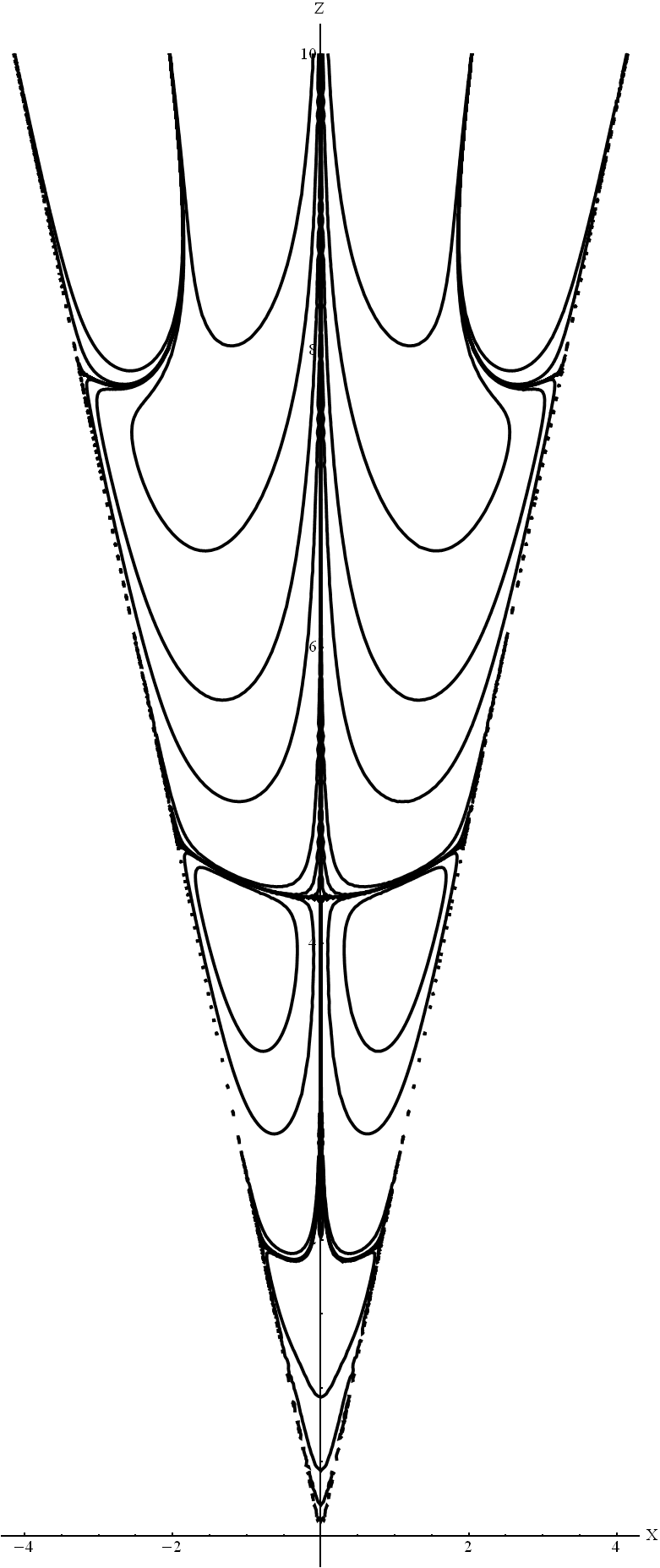
Рис. 4. Линии тока под воздействием стокслета, находящегося в точке в конусе с углом раствора

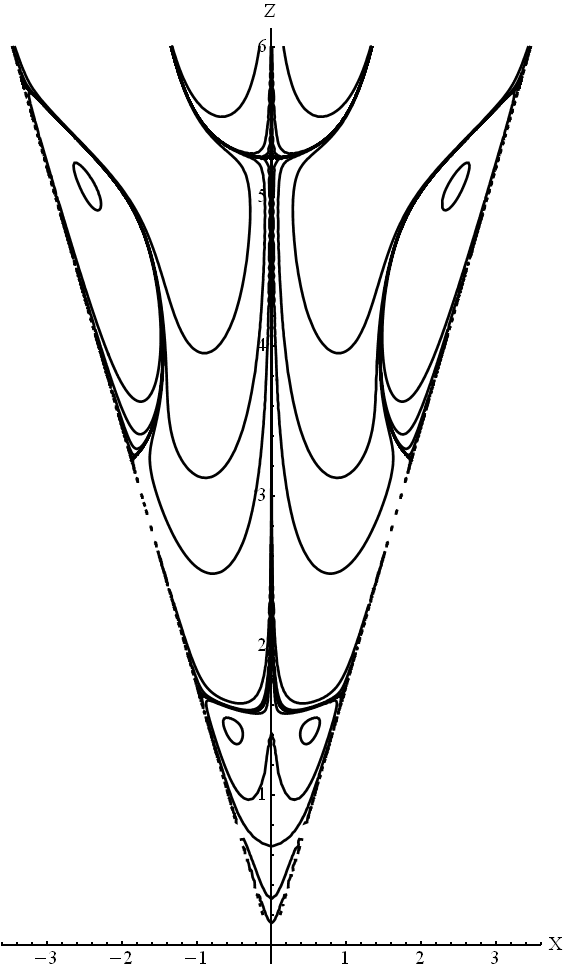
Рис. 5. Линии тока под воздействием стокслета, находящегося в точке в конусе с углом раствора

4. Выводы

В работе рассмотрен вопрос о движении жидкости в наноразмерном конусе. В результате моделирования движения жидкости в приближении Стокса было обнаружено образование вихрей. В [18] впервые была выявлена последовательность образующихся вихрей в остром угле. Позже подобное течение наблюдалось многими авторами, например, [5, 15, 19]. В данной работе рассматривалось осесимметричное течение внутри конуса под воздействием стокслета. Используемый метод позволяет получить функцию тока в некоторой ограниченной области относительно (область сходимости рядов). Получены картины линий тока для таких областей (Рис. 3-5), отличающихся друг от друга углом раствора конуса. Полученные результаты согласуются с результатами [16, 22, 12]. Можно заметить, что интенсивность вихрей существенно уменьшается с отдалением от вершины конуса. Сама картина течения зависит от выбранного вида стокслета (Рис. 2). Также важно отметить, что стокслет – не источник массы, а источник вихрей, поэтому в фиксированном объеме масса сохраняется. Клеточная структура течения характерна для потока Стокса. Для малых углов раствора конуса можно видеть вертикальную (по оси конуса) клеточную структуру в области, близкой к стокслету (Рис. 3-4). Для больших значений углов появляется горизонтальная ячеистая структура (Рис. 5).

Этот эффект может быть интересен с точки зрения нанохимических реакций. Экспериментально было обнаружено, что при течении в наноканалах происходит разделение компонентов жидкости ([10, 3]). Этот вопрос имеет ряд трактовок, однако, окончательно вопрос о природе химического разделения при течении в наноканале не решен. Решение вопроса об образовании вихрей в конической геометрии может способствовать построению теории течения многокомпонентных жидкостей, приводящего к их химическому разделению. Такая теория может стать основой для развития мембранной техники разделения компонентов с использованием наноканалов. Возможный ответ на этот вопрос: вихрь может быть причиной разделения компонент жидкости за счет их различной плотности. В свою очередь, он может вызывать химические реакции в разных частях вихря, то есть играть роль нанореактора.

Благодарности

Данная работа была поддержана программой «Развитие научного потенциала российской высшей школы» (проект 2.1.1/4215), «Научные кадры инновационной России» (контракты П689 НК-526П и 14.740.11.0879), грант РФБР 11-08-00267.

Список литературы

[1] Ackerberg R.C. The viscous incompressible flow inside a cone // J. Fluid Mech. 1965. 21, part 1. C. 47-81.

[2] Blake J.R. A note on the image system for a stokeslet in a no-slip boundary, Proc. Camb. Phil. Soc. 1971. 70, 303-10

[3] Chivilikhin S.A., Popov I.Yu. and Gusarov V.V. Planar flows in nanoscale regions // Nanosystems: Phys. Chem. Math. 2011. V.2(3). C.49-52.

[4] Gugel Yu.V., Popov I.Yu. and Popova S.L. Hydrotron: creep and slip // Fluid Dyn. Res. 1996. 18, 199.

[5] Hackborn W.W. Asymmetric Stokes flow between parallel planes due to a rotlet // J. Fluid Mech. 1990. 218. 531-46.

[6] Hall O., Gilbert A.D. and Hills C.P. Converging flow between coaxial cones // Fluid Dyn. Res. 2009. 41. 011402.

[7] Happel J. and Brenner H. 1965, Low Reynolds Number Hydrodynamics, (Prentice-Hall; Engle-wood Cliffs, N.J.)

[8] Hasimoto H. and Sano O. 1980 Stokeslets and eddies in creeping flow, Ann. Rev. Fluid Mech., 12, 335-363

[9] Kim M.U. 1977 Slow viscous rotation of a sphere on the axis of a circular cone, J. Korean Phys. Soc., 10, (2), 54-8

[10] Kononova S.V., Korytkova E.N., Romashkova K.A., Kuznetsov Yu.P., Gofman I.V., Svetlichnyi V.M., Gusarov V.V. 2007 Nanocomposite on the basis of amide imide resin with hydrosylicate nanoparticles of different morphology, J. Appl. Chem., 80, (12) 2064-70

[11] Korn G.A. and Korn T.M. 1968, Mathematical Handbook for Scientists and Engineers, (McGraw-Hill, New York)

[12] Lecoq N., Masmoudi K., Anthore R. and Feullebois F. 2007 Creeping motion of a sphere along the axis of a closed axisymmetric container, J. Fluid Mech., 585, 127-52

[13] Лебедев Н.Н. 1963, Специальные функции и их приложения (Второе издание), (М.-Л.: ГИФМЛ)

[14] Liron N. and Mochon S. 1976 Stokes flow for a stokeslet between two parallel flat plates, J. Eng. Math., 10, No. 4

[15] Liron N. and Shahar R. 1978 Stokes flow due to a stokeslet in a pipe, J. Fluid Mech., 86, part 4 727-44

[16] Liu C.H. and Joseph D.D. 1978 Stokes flow in conical trenches, SIAM J. Appl. Math., 34, No. 2

[17] Malyuga V.S. 2005 Viscous eddies in a circular cone, J. Fluid Mech., 522, 101-16

[18] Moffatt H.K. 1964 Viscous eddies near a sharp corner, Arch. Mech. Stosow., 2, 365-72

[19] Popov I.Yu. 1993 Operator extensions theory and eddies in creeping flow, Phys. Scr., 47, 682

[20] Popov I.Yu. 1996 Stokeslet and the operator extensions theory, Rev. Mat. Univ. Compl. Madrid, 9, (1) 235-58

[21] Pozrikidis C. 1996 Computation of periodic Green's functions of Stokes flow, J. Eng. Math., 30, 79-96

[22] Shankar P.N. 2005 Moffatt eddies in the cone, J. Fluid Mech., 539, 113-35

[23] Usha R. and Nigam S.D. 1993 Flow in a spherical cavity due to stokeslet, Fluid Dyn. Res., 11, 75-8

[24] Wakiya S. 1976 Axisymmetric flow of a viscous fluid near the vertex of a body, J . Fluid Mech., 78, 737-47