Разработка методов Метод инициализации линейного уравнения

I. Спецификация

1. Назначение: заполнение полей а1 (коэффициент при неизвестном х) и а0 (свободный член) исходными данными.

2. Имя: INIT

3. Вид: процедура

4. Перечень параметров (все параметры входные):

Назначение	Имя	Тип	Вид
Значение коэффициента при неизвестном х	a	real	параметр-значение
Значение свободного члена	b	real	параметр-значение

5. Заголовок: PROCEDURE INIT(a,b:REAL);

II. Метод решения

1. a1:=a

2. a0:=b

V. Программная модель

procedure tlinur.init(a,b:real);

begin

a1:=a;

a0:=b

end;

Метод решения линейного уравнения

I. Спецификация

1. Назначение: решение линейного уравнения вида a₁x+a₀=0 для любых вещественных a₁ и a₀

2. Имя: LINUR

3. Вид: процедура

4. Перечень параметров: без параметров

5. Заголовок: PROCEDURE LINUR;

II. Метод решения

V. Программная модель

procedure tlinur.linur;

begin

if a1<>0 then

begin

k:=1;

x1:=-a0/a1

end

else

if a0=0 then k:=-1

else k:=0

end;

Метод вывода решения линейного уравнения

I. Спецификация

1. Назначение: вывод на экран результатов решения линейного уравнения

1. Имя: PRINT

2. Вид: процедура

3. Перечень параметров: без параметров

4. Заголовок: PROCEDURE PRINT;

II. Метод решения

выбор по значению k из вариантов

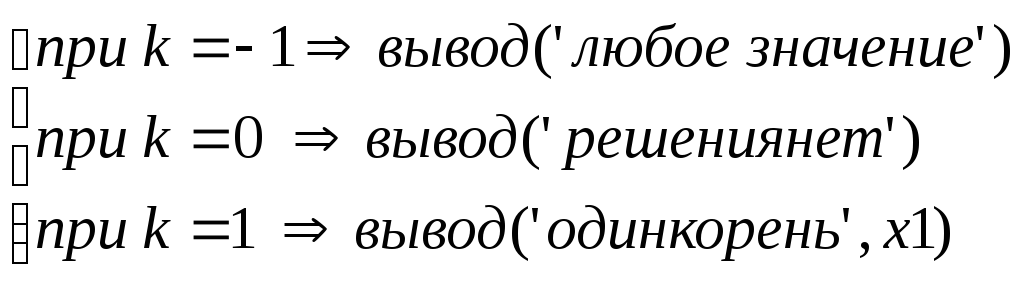
V. Программная модель

procedure tlinur.print;

begin

case k of

-1:writeln('любое значение');

0:writeln('решений нет');

1: writeln('один корень=',x1)

end

end;

Метод инициализации квадратного уравнения

I. Спецификация

1. Назначение: заполнение полей а2 (коэффициент при квадрате х), а1 (коэффициент при неизвестном х) и а0 (свободный член) исходными данными.

2. Имя: INIT

3. Вид: процедура

4. Перечень параметров (все параметры входные):

Назначение	Имя	Тип	Вид
Значение коэффициента при квадрате неизвестного x	a	real	параметр-значение
Значение коэффициента при неизвестном х	b	real	параметр-значение
Значение свободного члена	с	real	параметр-значение

5. Заголовок: PROCEDURE INIT(a,b,c:REAL);

II. Метод решения

1. a2:=a

2. a1:=b

3. a0:=c

V. Программная модель

procedure tkvur.init(a,b,c:real);

begin

a2:=a;

a1:=b;

a0:=c

end;

Метод решения квадратного уравнения

I. Спецификация

1. Назначение: решение квадратного уравнения вида a₂x²+a₁x+a₀=0 в области вещественных чисел.

2. Имя: KVUR

3. Вид: процедура

4. Перечень параметров: без параметров

5. Заголовок: PROCEDURE KVUR;

II. Метод решения

III. Информационная модель

Назначение	Имя	Тип
Дискриминант	d	real

V. Программная модель

procedure tkvur.kvur;

var d:real;

begin

if a2<>0 then

begin

d:=(sqr(a1)-4*a2*a0);

if d>=0 then

begin

x1:=(-a1+sqrt(d))/(2*a2);

x2:=(-a1-sqrt(d))/(2*a2);

k:=2

end

else

k:=0

end

else linur

end;

Метод вывода решения квадратного уравнения

I. Спецификация

1. Назначение: вывод на экран результатов решения квадратного уравнения

1. Имя: PRINT2

2. Вид: процедура

3. Перечень параметров: без параметров

4. Заголовок: PROCEDURE PRINT2;

II. Метод решения

выбор по значению k из вариантов

V. Программная модель

procedure tkvur.print2;

begin

case k of

-1..1:print;

2:writeln('два корня x1=',x1,' x2=',x2)

end

end;

Метод решения биквадратного уравнения

I. Спецификация

1. Назначение: решение биквадратного уравнения вида a₂x⁴+a₁x²+a₀=0 в области вещественных чисел.

2. Имя: BIKVUR

3. Вид: процедура

4. Перечень параметров: без параметров

5. Заголовок: PROCEDURE BIKVUR;

II. Метод решения

1. Вычисляем квадраты возможных корней, для этого решаем биквадратное уравнение как квадратное

KVUR ;

2. В зависимости от количества полученных корней продолжаем решение. В зависимости от полученного значения k вычисляем корни

Выбор по значению k из вариантов

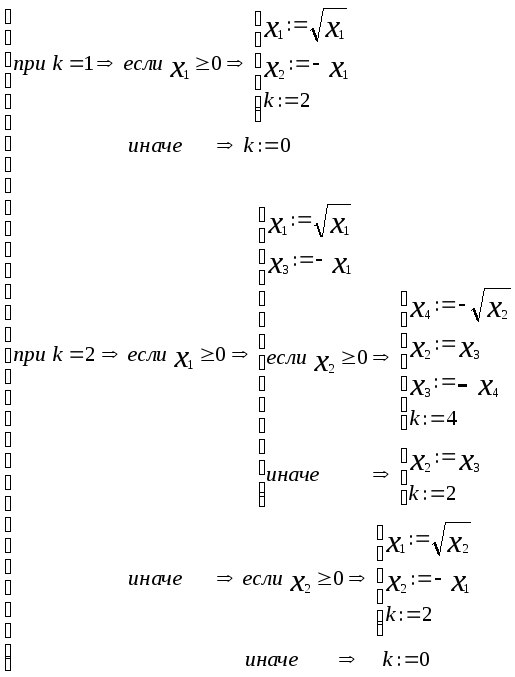
III. Информационная модель

Назначение	Имя	Тип
Дискриминант	d	real

V. Программная модель

procedure tbikvur.bikvur;

begin

kvur;

case k of

1: if x1>=0 then

begin

x1:=sqrt(x1);

x2:=-x1;

k:=2

end

else k:=0;

2: if x1>=0 then

begin

x1:=sqrt(x1);

x3:=-x1;

if x2>=0 then

begin

x4:=-sqrt(x2);

x2:=x3;

x3:=-x4;

k:=4

end

else

begin

x2:=x3;

k:=2

end

end

else

if x2>=0 then

begin

x1:=sqrt(x2);

x2:=-x1;

k:=2

end

else k:=0

end

end;

Метод вывода решения биквадратного уравнения

I. Спецификация

1. Назначение: вывод на экран результатов решения биквадратного уравнения

1. Имя: PRINT4

2. Вид: процедура

3. Перечень параметров: без параметров

4. Заголовок: PROCEDURE PRINT4;

II. Метод решения

выбор по значению k из вариантов

V. Программная модель

procedure tbikvur.print4;

begin

case k of

-1..2:print2;

4:writeln('четыре корня x1=',x1,' x2=',x2,' x3=',x3,' x4=',x4)

end

end;

8