Лекция № 4

Все геометрические параметры эвольвентного цилиндрического зубчатого колеса приведены на рис. 4.1:

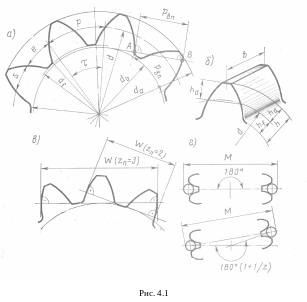
4.1. Основные геометрические параметры эвольвентного цилиндрического зубчатого колеса

- расстояние между разноимёнными профилями зуба по дуге делительной окружности;

- расстояние между профилями впадин соседних зубьев;

- расстояние между одноимёнными профилями соседних зубьев по дуге делительной окружности (окружной шаг);

- центральный угол делительной окружности ( - угловой шаг);

- линейная величина, в раз меньшая окружного шага (окружной модуль);

- наименьшее расстояние между торцами зубьев (ширина венца);

- расстояние между окружностями вершин и впадин (высота зуба);

- высота делительной головки зуба;

- высота делительной ножки зуба;

- шаг зубьев колеса по основной окружности;

- диаметры: делительной окружности, впадин, основной окружности и вершин соответственно.

4.2. Виды зубчатых колёс в зависимости от толщины зуба по делительной окружности

Окружной шаг зубьев колеса по любой окружности вычисляется по формуле:

Конструктор для колёс одного и того же модуля может предусматривать различные значения толщины зубьев по делительной окружности.

В общем случае:

, где: - изменение толщины зуба; - коэффициент изменения толщины зуба.

По значению коэффициента изменения толщины зуба для внешнего зацепления различают колёса трёх видов:

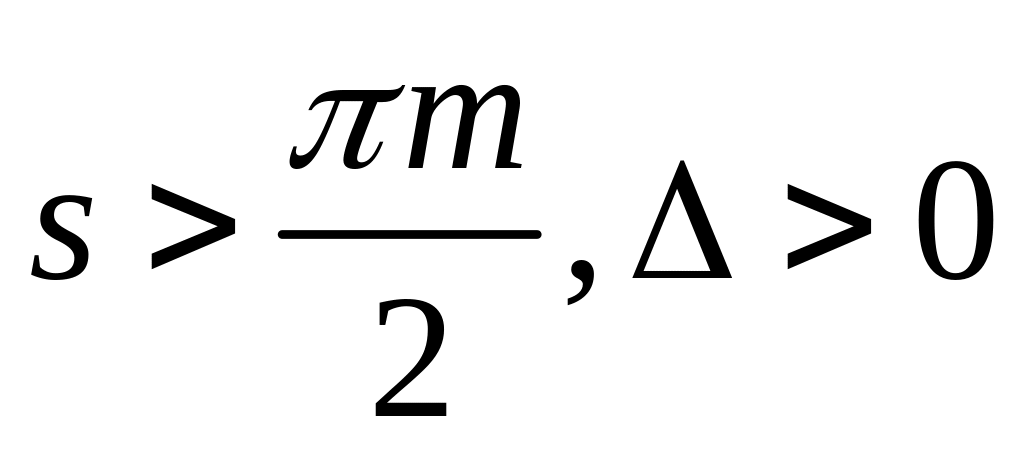1. - колесо положительное;

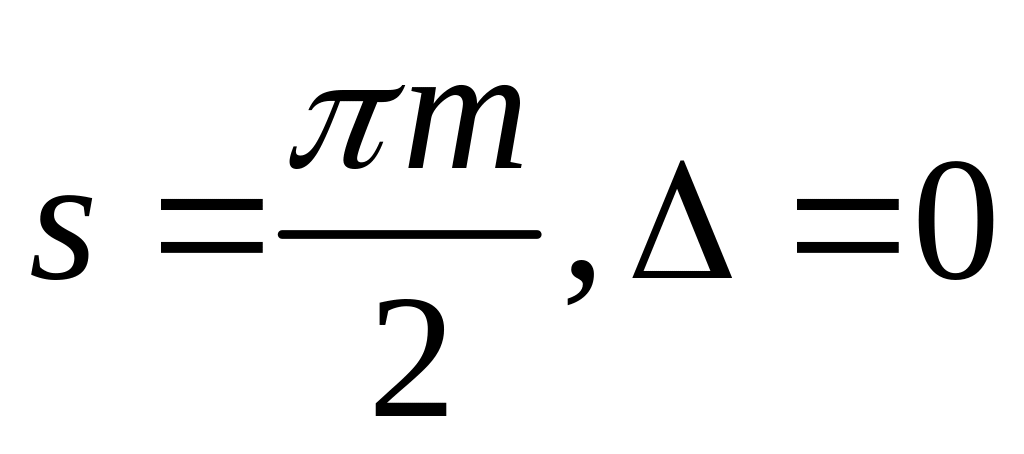2. - колесо нулевое;

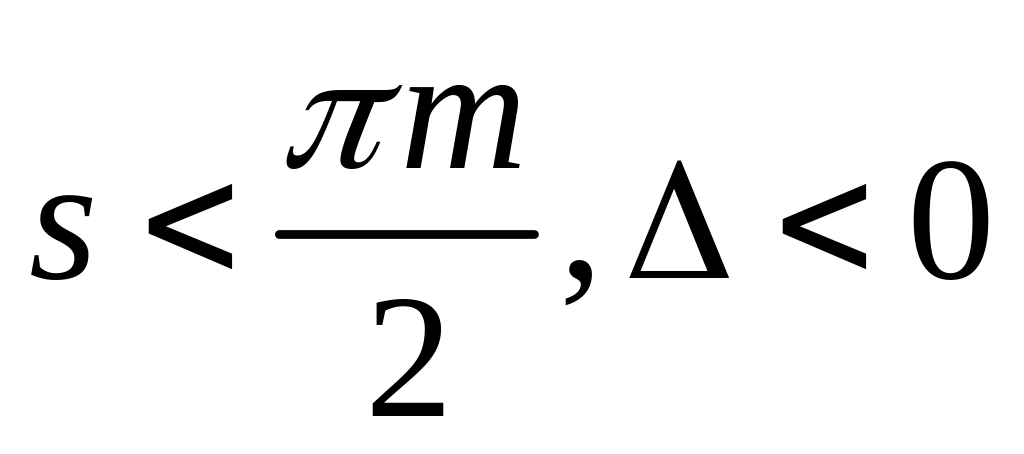3. - колесо отрицательное.

Чаще всего применяют нулевые колёса. Положительные колёса применяются в силовых передачах. Для нулевых колёс высота делительной головки зуба определяется следующим образом:

[мм]

В приборостроении применяются модули мм.

За счёт разности высот ножки и головки зубьев обеспечивается радиальный зазор зубчатой передачи.

Для зубчатых колёс установлены параметры, по которым их проверяют в процессе изготовления:

1. - длина общей нормали;

2. - расстояние между выступающими в радиальном направлении поверхностями вершин двух шариков, опирающихся на боковые поверхности зубьев.

4.3. Элементы и параметры двух нулевых колёс эвольвентного профиля

Основным условием зацепления является равенство модулей, а, следовательно, и шагов . Зубчатое колесо с меньшим числом зубьев в зацеплении – шестерня (если колёса имеют равное число зубьев, то шестернёй называют ведущее колесо).

Рассмотрим рис. 4.2:

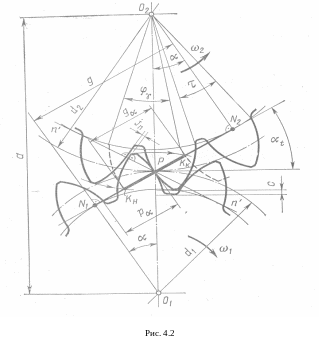
- линия зацепления (траектория общей точки контакта зубьев К при вращении колёс;

- теоретическая длина линии зацепления;

- (активная) длина на активной линии зацепления;

- шаг эвольвентного зацепления;

- угол зацепления (угол между линией зацепления и прямой, перпендикулярной межосевой линии);

- угол поворота зубчатого колеса от положения входа в зацепление в точке до положения выхода в точке ;

- угловой шаг зубьев;

- коэффициент перекрытия зубчатой передачи ( ).

При вращении зубчатых колёс в них существуют окружности, которые катятся друг по другу без скольжения. Эти окружности обозначают и . Они являются центроидами относительного движения колёс. Это начальные окружности.

Начальные и делительные окружности у нулевых колёс совпадают, однако между ними существует различие: делительная окружность – геометрический параметр колеса , а начальная окружность – понятие кинематическое, имеющее смысл только для колёс, находящихся в зацеплении.

Межосевое расстояние по начальным окружностям определяется по формуле:

.

Межосевое расстояние по делительным окружностям определяется, исходя из следующего соотношения:

.

В общем случае:

Полюс зацепления Р принадлежит прямой . Если колёса поворачивать, полюс зацепления остаётся на этой же линии. Следовательно, общая нормаль одновременно является и касательной к основным окружностям и линией зацепления ( - траектория точки контакта от начала до конца зацепления)

- реальная длина линии зацепления.

Коэффициент перекрытия зубчатой передачи показывает среднее число пар зубьев, находящихся одновременно в зацеплении. Непрерывность нормальной работы зубчатой передачи возможна при условии, когда последующая пара зубьев входит в зацепление до выхода из зацепления предыдущей пары. То есть, когда обеспечивается перекрытие работы одной пары зубьев другой. При этом . В случае, когда , зубчатая передача будет работать с ударами.

Боковой зазор (нормальный) определяется как расстояние по общей нормали между неконтактирующими профилями, находящихся в зацеплении.

Радиальный зазор С зубчатой передачи – наименьшее расстояние между поверхностью вершин одного колеса и поверхностью впадин другого.