
- •Лекция № 1
- •Механические передачи.
- •1.2. Кинематические характеристики передач
- •1.3. Силовое исследование передач
- •1.4. Динамические исследования передач
- •1.5. Основные характеристики и параметры приборных электродвигателей
- •1.6. Многоступенчатые зубчатые передачи. Основные понятия.
- •Виды передач в редукторе
- •1.7. Классификация многоступенчатых зубчатых передач.
- •Зубчатые передачи
- •2.1. Классификация
- •2.2. Основные понятия
- •2.3. Основные параметры
- •2.4. Основная теорема зацепления
- •2.5. Общие требования к профилям зубьев
- •Лекция № 3
- •3.1. Цилиндрическая эвольвентная зубчатая передача
- •3.2. Выбор участка эвольвенты для профиля зуба колеса
- •Лекция № 4
- •4.1. Основные геометрические параметры эвольвентного цилиндрического зубчатого колеса
- •4.2. Виды зубчатых колёс в зависимости от толщины зуба по делительной окружности
- •4.3. Элементы и параметры двух нулевых колёс эвольвентного профиля
- •4.4. Основные свойства эвольвентного зацепления
- •Лекция № 5
- •5.1. Методы нарезания зубьев колёс
- •5.2. Интерференция в эвольвентном зацеплении
- •5.3. Определение минимального числа зубьев колеса из условия предупреждения интерференции
- •5.4. Коррегирование эвольвентного зацепления
- •Лекция № 6 Расчёты зубчатых колёс на прочность.
- •Виды повреждений зубьев
- •6.2. Силовые соотношения в прямозубых эвольвентных зубчатых передачах
- •6.3. Расчёт зубчатых передач на изгиб зубьев
- •6.5. Эвольвентные зубчатые передачи с внутренним зацеплением зубьев.
- •Лекция № 7
- •7.1. Косозубые цилиндрические колёса. Геометрические параметры
- •7.2. Коэффициент торцевого перекрытия
- •7.3. Расчёт косозубых колёс на прочность
- •Лекция № 8
- •8.1. Конические зубчатые передачи. Геометрические и кинематические соотношения
- •8.2. Особенности расчёта на прочность конических прямозубых передач
Лекция № 6 Расчёты зубчатых колёс на прочность.
Виды повреждений зубьев
Практика эксплуатации зубчатых передач показывает, что основными причинами повреждений зубьев являются неправильный расчёт, низкое качество изготовления и сборки, нарушения правил эксплуатации.
Поломка зубьев при статических и динамических перегрузках.
Зуб отламывается у основания. При многократно меняющей знак нагрузке зуб ломается вследствие появления трещин. Виды повреждений зависят от вида передач (открытые и закрытые передачи). Закрытые передачи работают в герметически закрытом и наполненном маслом корпусе. Открытые передачи либо совсем незакрыты, либо имеют кожух, защищающий от пыли и влаги.
2. Выкрашивание поверхности зубьев.
Чаще всего проявляется в закрытых передачах. При знакопеременных нагрузках появляются трещины. При контакте зубьев масло, попадая в трещины, работает как клин. Это явление называется питтингом.
3. Абразивный износ получается в передачах, работающих в загрязнённой атмосфере. В результате износа возникают большие зазоры, приводящие к появлению ударов.
4. Заедание зубьев.
Наблюдается при увеличении шага и скорости. В этом случае зубья нагреваются и получается «местное приваривание» с дальнейшим отрывом. В таких передачах проводят расчёт на нагрев.
5. Повреждение торцёв колёс.
Наблюдается в коробках скоростей при включении и выключении колёс на ходу. В этом случае рекомендуется использовать синхронизаторы вращения.
6. Пластическая текучесть материала.
Наблюдается в нагруженных передачах при небольших скоростях. Вблизи полюса зацепления на зубьях возникают складки. Проявляется чаще в машиностроении.
С учётом особенностей открытых и закрытых передач расчёты производятся в следующей последовательности: для открытых передач расчёт зубьев на изгиб и проверочный расчёт на контактную прочность, а для закрытых – расчёт зубьев на контактную прочность и проверочный расчёт зубьев на изгиб.
6.2. Силовые соотношения в прямозубых эвольвентных зубчатых передачах
Рассмотрим рис. 6.1:
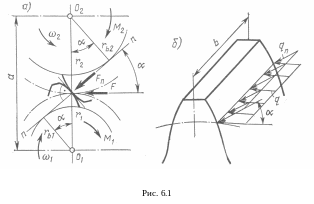
![]() - нормальная распределённая нагрузка;
- нормальная распределённая нагрузка;
![]() - нормальная сила;
- нормальная сила;
![]() - нормальная расчётная сила, учитывающая
дополнительные нагрузки;
- нормальная расчётная сила, учитывающая
дополнительные нагрузки;
![]() - коэффициент нагрузки (
- коэффициент нагрузки (![]() );
);
![]() - коэффициент концентрации нагрузки
(неточность изготовления колёс, наличие
упругих деформаций, толчков и ударов в
процессе зацепления);
- коэффициент концентрации нагрузки
(неточность изготовления колёс, наличие
упругих деформаций, толчков и ударов в
процессе зацепления);
![]() - коэффициент динамичности нагрузки
(влияние инерции зубчатых колёс,
возникающей при пусках, разгонах,
торможении и остановке).
- коэффициент динамичности нагрузки
(влияние инерции зубчатых колёс,
возникающей при пусках, разгонах,
торможении и остановке).
Нормальная распределённая нагрузка определяется по формуле:
![]() ;
;
![]() .
.
Нормальная расчётная сила определяется по формуле:
![]() ,
где
,
где
![]() .
.
6.3. Расчёт зубчатых передач на изгиб зубьев
Принимаем, что известны числа
зубьев
и
![]() колёс передачи и момент нагрузки
колёс передачи и момент нагрузки
![]() на ведомом колесе. Неизвестным является
модуль
,
от которого зависит геометрический
размер колёс. Для его определения
рассмотрим расчётную схему (рис. 6.2),
соответствующую случаю, когда напряжения
в основании зуба наибольшие.
на ведомом колесе. Неизвестным является
модуль
,
от которого зависит геометрический
размер колёс. Для его определения
рассмотрим расчётную схему (рис. 6.2),
соответствующую случаю, когда напряжения
в основании зуба наибольшие.
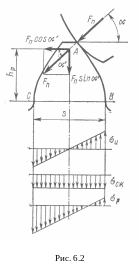
Принимаем, что расчётная сила
приложена вдоль линии зацепления в
вершине зуба. Считаем, что сила трения
![]() пренебрежимо мала, и в зацеплении
находится один зуб. Зуб рассматривается
как консольная балка, защемлённая у
основания.
пренебрежимо мала, и в зацеплении
находится один зуб. Зуб рассматривается
как консольная балка, защемлённая у
основания.
Неточность расчёта компенсируется эмпирическими коэффициентами.
Расчёт ведётся для наихудшего случая,
который соответствует приложению
расчётной силы
в точке
![]() ,
так как именно в этот момент плечо
изгибающего момента максимально. Для
упрощения вычислений принимают
коэффициент перекрытия
,
так как именно в этот момент плечо
изгибающего момента максимально. Для
упрощения вычислений принимают
коэффициент перекрытия
![]() равным единице. Приложение силы
переместим в точку
равным единице. Приложение силы
переместим в точку
![]() на оси симметрии зуба.
на оси симметрии зуба.
В проекциях на ось симметрии зуба можем получить:
![]() - изгибающая сила;
- изгибающая сила;
![]() - сжимающая сила.
- сжимающая сила.
Обозначим плечо, на котором действует
сила за
![]() .
.
Для дальнейшего упрощения
![]() заменяют условной касательной силой
,
действующей на делительные окружности
в процессе передачи крутящего момента
ведущим колесом.
заменяют условной касательной силой
,
действующей на делительные окружности
в процессе передачи крутящего момента
ведущим колесом.
![]() ,
,
где
![]() .
.
Эпюры напряжений изгиба
![]() ,
сжатия
,
сжатия
![]() и результирующего напряжения
и результирующего напряжения
![]() показаны на рис. 6.2.
показаны на рис. 6.2.
Расчёт ведём по результирующему напряжению в волокнам материала, испытывающих растяжение, то есть для точки . Опыт показывает, что именно в этом месте зуба начинается его разрушение, приводящее к излому, несмотря на то, что с противоположной стороны напряжения по абсолютному значению больше (напряжения сжатия материала зуба).
Результирующее напряжение в точке :
![]() .
.
- изгибающий момент от силы
![]() ;
;
![]() - угол профиля зуба в вершине, отличающийся
от угла в точке профиля зуба на делительной
окружности;
- угол профиля зуба в вершине, отличающийся
от угла в точке профиля зуба на делительной
окружности;
- длина зуба (ширина зубчатого венца колеса);
- толщина зуба в опасном сечении.
Учитывая, что
![]() и
и
![]() ,
получаем:
,
получаем:
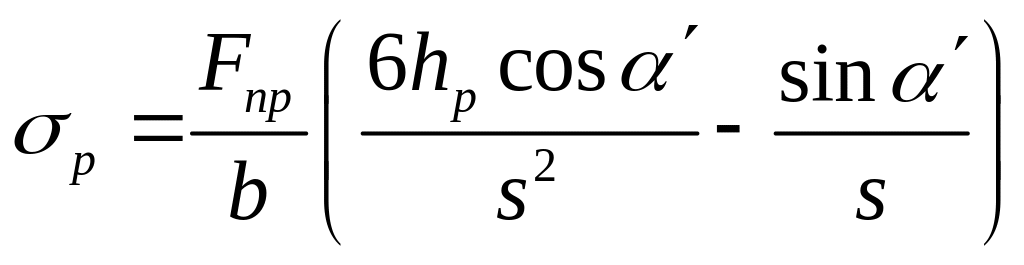 .
.
Произведём замену силы
моментом
,
и
![]() и умножим правую часть выражения на
и умножим правую часть выражения на
![]() :
:
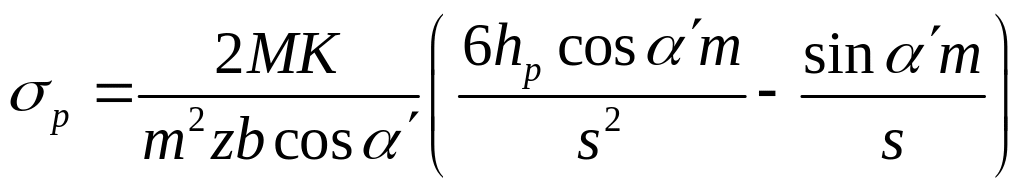 .
.
Величина в скобках числителя безразмерная. Она зависит от числа зубьев и смещения инструмента, изменяющего толщину зуба в опасном сечении. В связи с этим выражение, входящее в предыдущую формулу:
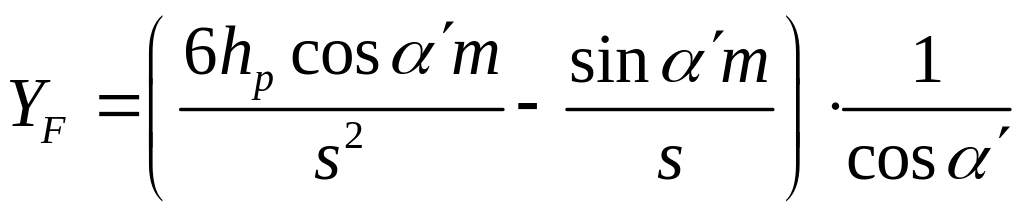 ,
называют
коэффициентом прочности зуба.
,
называют
коэффициентом прочности зуба.
Вводя этот коэффициент, получаем:
![]() .
.
Произведём замену
![]() ,
тогда:
,
тогда:
![]() .
.
Формулу используют при проверочных расчётах, когда имеется возможность применить готовую передачу с известными размерами.
Находим выражение для модуля:
![]() .
.
Полученную формулу используют при проектировочных расчётах.
Коэффициент
![]() для прямозубых колёс;
для прямозубых колёс;
![]() для косозубых колёс.
для косозубых колёс.
Значения коэффициента прочности зуба
![]() можно определить по таблицам в зависимости
от числа зубьев колеса и коэффициента
смещения исходного контура.
можно определить по таблицам в зависимости
от числа зубьев колеса и коэффициента
смещения исходного контура.
\ 6.4. Расчёт зубчатых колёс на контактную прочность
Расчёт ведётся для закрытых зубчатых передач, то есть передач, помещённых в корпусе со смазывающей жидкостью. Исходной является формула Герца для подсчёта контактных напряжений при контакте деталей по цилиндрическим поверхностям:
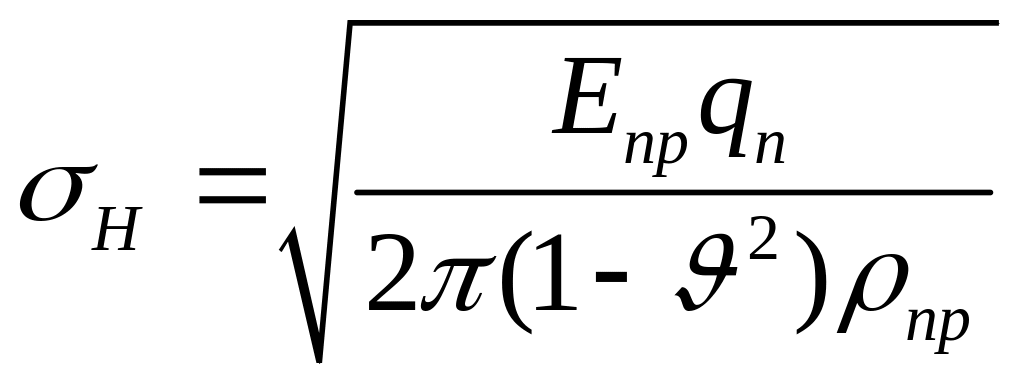 ,
где
- давление, нормальное к поверхности
зуба;
,
где
- давление, нормальное к поверхности
зуба;
![]() - приведённый модуль упругости;
- приведённый модуль упругости;
![]() - приведённый радиус кривизны;
- приведённый радиус кривизны;
![]() -
коэффициент Пуассона.
-
коэффициент Пуассона.
Из накопленного опыта эксплуатации зубчатых передач следует, что наибольший износ поверхности зубьев происходит в зоне полюса зацепления. Рассмотрим расчётную схему, соответствующую этому случаю (рис. 6.3):
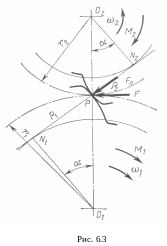
Обозначим
момент сопротивления нагрузки. Вывод
формулы расчёта
![]() произведём для случая, когда
произведём для случая, когда
![]() ,
,
,
,
![]() и
и
![]() .
Контакт зубьев в полюсе зацепления
можно рассматривать как контакт
цилиндрических поверхностей, имеющих
радиусы эвольвент в точке
.
Контакт зубьев в полюсе зацепления
можно рассматривать как контакт
цилиндрических поверхностей, имеющих
радиусы эвольвент в точке
![]() и
и
![]() .
.
Подсчитаем
![]() ,
выразив предварительно
и
через
,
выразив предварительно
и
через
![]() ,
,
![]() и
:
и
:
![]() ;
;
![]() ;
;
![]() .
.
Учитывая, что задано передаточное отношение, введём его в полученную формулу.
![]() .
.
Для этого заменим
и
на
![]() и
.
Решая их относительно
и
,
получаем:
и
.
Решая их относительно
и
,
получаем:
![]() ;
;
![]() .
.
Учитывая полученные значения, можно выразить :
![]() .
.
Подставляем полученное значение в формулу Герца:
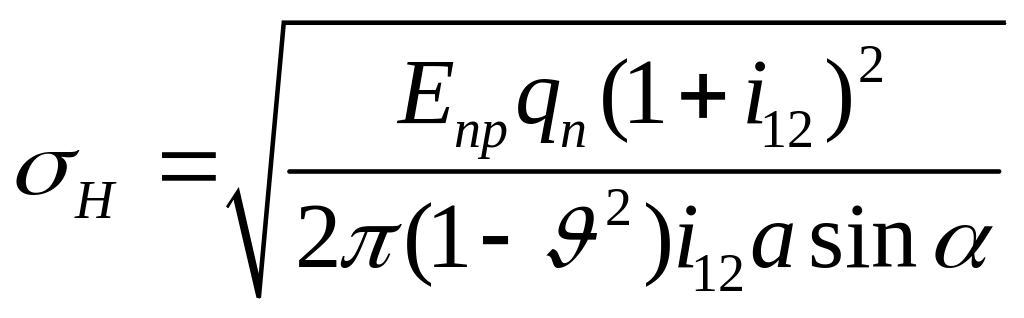 .
.
Заменяем нормальное давление
окружным
![]() :
:
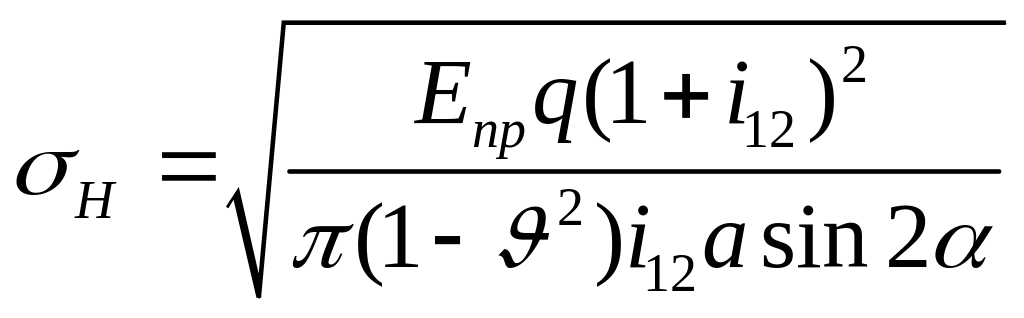 .
.
Заменим величину через момент :
![]() ,
,
тогда:
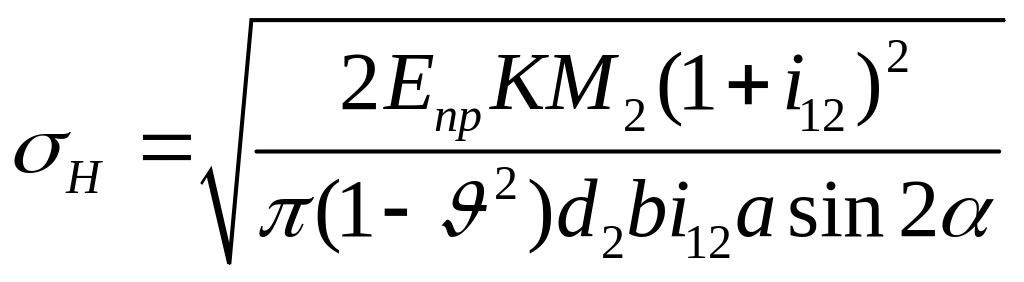
Введём в формулу коэффициенты:
![]() - коэффициент, учитывающий форму
соприкасающихся поверхностей:
- коэффициент, учитывающий форму
соприкасающихся поверхностей:
![]() (при
(при
![]() );
);
![]() - коэффициент, учитывающий механические
свойства материалов колёс:
- коэффициент, учитывающий механические
свойства материалов колёс:
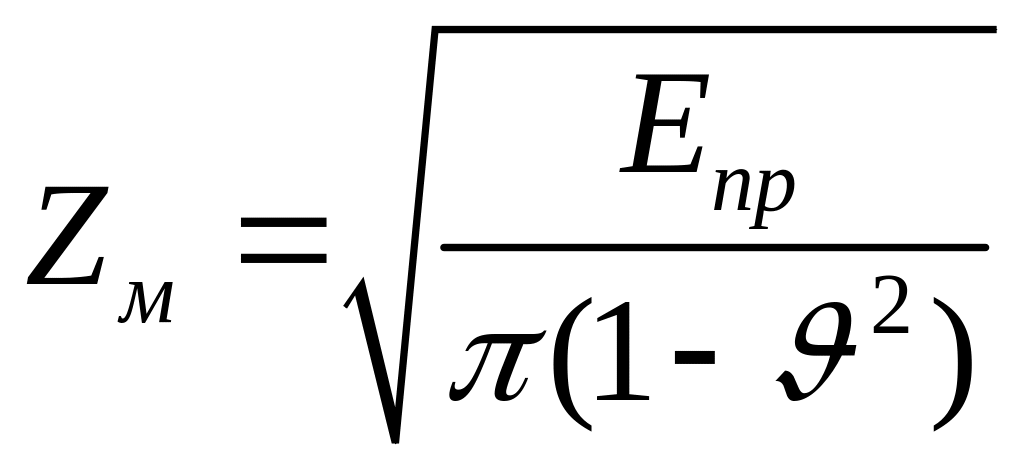 ;
;
![]() - коэффициент, учитывающий влияние
торцевого перекрытия зубьев (для приборов
средней точности расчёта принимают
- коэффициент, учитывающий влияние
торцевого перекрытия зубьев (для приборов
средней точности расчёта принимают
![]() ).
).
Получим:
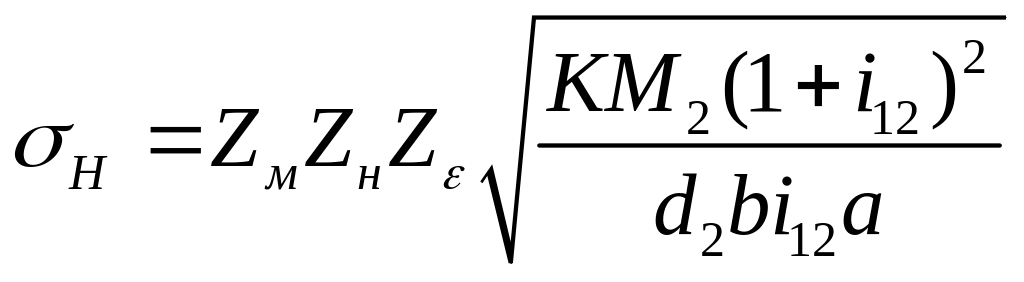 .
.
Будем исходить из условия, что
![]() ,
где
,
где
![]() известно. Тогда получим:
известно. Тогда получим:
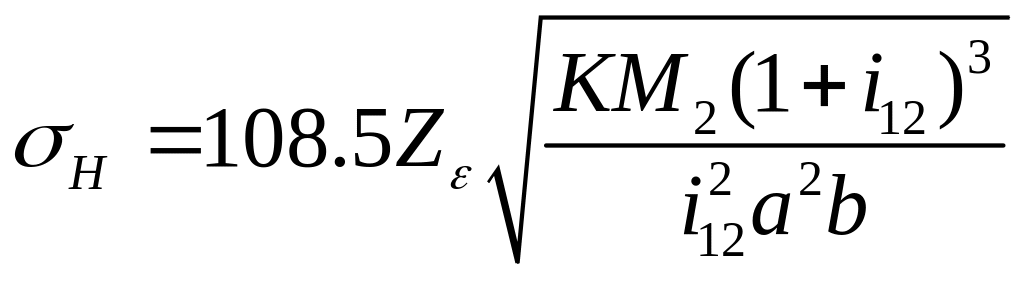 .
.
Задаемся отношением ширины венца колеса
к межосевому расстоянию, то есть
![]() ,
тогда получаем формулу, которую используют
для проверочного расчёта:
,
тогда получаем формулу, которую используют
для проверочного расчёта:
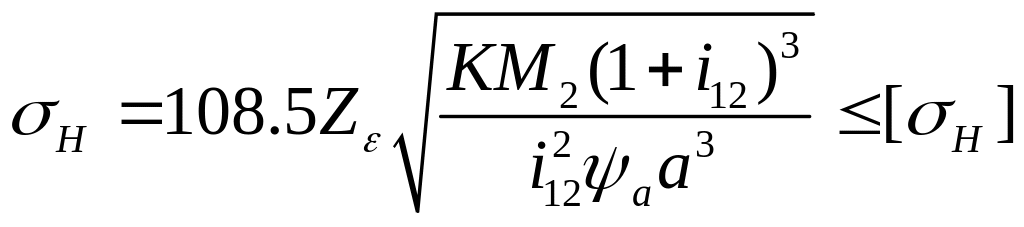 .
.
Отсюда получаем формулу для определения межосевого расстояния, которая применяется при проектировочном расчёте:
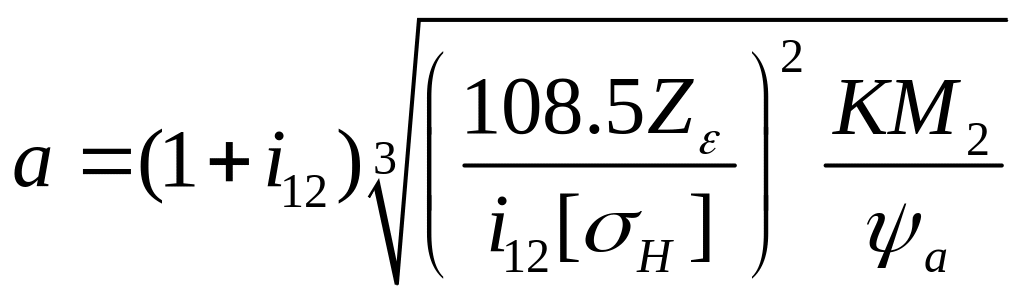 .
.
