
- •Статистические распределения квантовых газов
- •Большое каноническое распределение
- •Распределение Ферми–Дирака
- •Распределение Бозе–Эйнштейна
- •Для среднего числа бозонов в состоянии с энергией получаем распределение Бозе–Эйнштейна
- •Распределения частиц в классических и квантовых системах
- •Распределения (4.8), (4.10) и (4.12) объединяет формула
- •Электронный газ металла и полупроводника
- •Трехмерный электронный газ
- •Ферми-поверхности металлов
- •Двумерный электронный газ
- •Одномерный электронный газ
- •Квантование сопротивления баллистического проводника
- •Примеры
Распределение Ферми–Дирака
Среднее число фермионов в одном состоянии. По принципу Паули в одном состоянии может быть не более одного фермиона, тогда
![]() .
.
Из (4.5а) и (4.6) находим
 ,
,
 .
.
Для среднего числа фермионов в состоянии с энергией получаем распределение Ферми–Дирака
 .
(4.8)
.
(4.8)
Уровень
и энергия Ферми.
Из (4.8) при
![]() с учетом
с учетом
![]() ,
,

следует показанная пунктиром на рис. а ступенчатая функция
![]() .
(4.8а)
.
(4.8а)


а б
При
уровни с энергией
![]() заполнены полностью, уровни
заполнены полностью, уровни
![]() свободные,
как показано для электронов на рис. б.
Наибольшая энергия при
называется энергией
Ферми F,
соответствующий уровень – уровнем
Ферми. При
добавлении электрона в систему, согласно
принципу Паули, он занимает свободное
состояние вблизи уровня Ферми. Энергия
системы увеличивается на F.
Химический
потенциал равен средней энергии
добавляемой частицы,
тогда
свободные,
как показано для электронов на рис. б.
Наибольшая энергия при
называется энергией
Ферми F,
соответствующий уровень – уровнем
Ферми. При
добавлении электрона в систему, согласно
принципу Паули, он занимает свободное
состояние вблизи уровня Ферми. Энергия
системы увеличивается на F.
Химический
потенциал равен средней энергии
добавляемой частицы,
тогда
![]() .
.
При
![]() тепловое движение перебрасывает частицы
через уровень Ферми и они занимают
уровни с большей энергией, освобождая
уровни с меньшей энергией. Для оценки
переходной области вычисляем производную
распределения по энергии. Из (4.8) при
тепловое движение перебрасывает частицы
через уровень Ферми и они занимают
уровни с большей энергией, освобождая
уровни с меньшей энергией. Для оценки
переходной области вычисляем производную
распределения по энергии. Из (4.8) при
![]() получаем
получаем
 ,
,
где
угол
показан на рис. а.
Ширина
переходной области
 увеличивается
с ростом температуры.
При любой температуре
увеличивается
с ростом температуры.
При любой температуре
![]() .
(4.8б)
.
(4.8б)
Химический потенциал фермионов равен энергии состояния со степенью заполнения 1/2.
Распределение Бозе–Эйнштейна
Среднее число бозонов в одном состоянии. Для бозонов возможное число частиц в одном состоянии
![]()
Из (4.5а) получаем
 .
.
Геометрическая
прогрессия сходится, если основание
прогрессии
![]() ,
тогда
,
тогда
![]() .
Считаем энергии уровней
.
Считаем энергии уровней
![]() ,
тогда химический
потенциал бозонов не может быть
положительным
,
тогда химический
потенциал бозонов не может быть
положительным
![]() .
(4.9)
.
(4.9)
По формуле геометрической прогрессии

получаем статистическую сумму
 ,
,
 .
.
Из (4.7) в виде

находим
 .
.
Для среднего числа бозонов в состоянии с энергией получаем распределение Бозе–Эйнштейна
 .
(4.10)
.
(4.10)
Условие
обеспечивает
![]() при любой энергии и температуре. При
при любой энергии и температуре. При
![]() получаем
получаем
 .
(4.11)
.
(4.11)
Распределения частиц в классических и квантовых системах
Распределение классических частиц по энергии, выраженное через химический потенциал , имеет вид (2.62в)
 .
.
Учитывая плотность состояний классического газа (3.8а)
 ,
,
находим среднее число частиц в состоянии с энергией , т. е. распределение Максвелла–Больцмана
 .
(4.12)
.
(4.12)
Распределения (4.8), (4.10) и (4.12) объединяет формула
 ,
(4.13)
,
(4.13)
где


Распределения Максвелла (М),
Бозе–Эйнштейна (Б), Ферми–Дирака (Ф)
Квантовые распределения (4.8) и (4.10) переходят в классическое распределение (4.12) при
![]() ,
,
тогда
![]() .
.
Используя активность
![]() ,
,
для классической системы получаем
![]() ,
,
![]() ,
,
![]() .
(4.14)
.
(4.14)
Химический потенциал системы. Если частица имеет сохраняющийся заряд – электрический, и/или барионный, и/или лептонный, то число частиц в изолированной системе не изменяется в силу закона сохранения заряда. Тогда химический потенциал определяется из условия нормировки распределения на число частиц системы. Используя
![]() ,
,
получаем число частиц
 ,
(4.15)
,
(4.15)
где n – концентрация частиц. Учитывая плотность состояний трехмерного газа (3.8а)
![]() ,
,
где
 ,
,
и распределение (4.13), получаем концентрацию
 .
(4.16)
.
(4.16)
Химический
потенциал зависит от массы частицы m,
от числа спиновых состояний NS,
от концентрации n,
от температуры T,
от рода газа
![]() и от размерности координатного
пространства, в котором находится газ.
и от размерности координатного
пространства, в котором находится газ.

Химический потенциал трехмерного газа фермионов
Виды фермионного газа:
– Невырожденный газ близок к классическому газу;
– Вырожденный газ проявляет квантовые свойства.
Невырожденный
газ описывается
распределением Максвелла.
Для получения химического потенциала
используем (4.16) при
![]()
 ,
,
где учтено
 .
.
Откуда находим
 ,
,
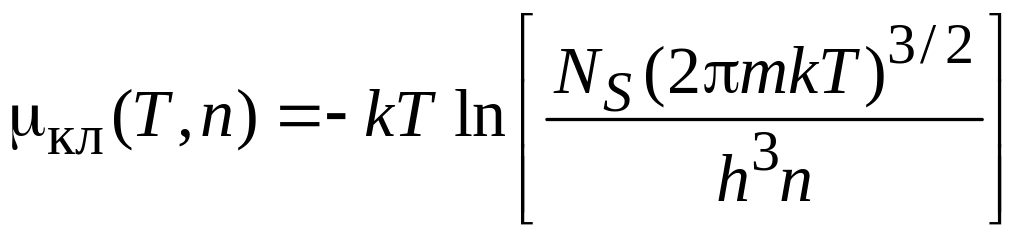 .
(4.17)
.
(4.17)
Химический
потенциал невырожденного газа
отрицательный, увеличивается с понижением
температуры и с ростом концентрации
частиц.
При
![]() результат совпадает с химическим
потенциалом (2.62а) классического газа.
Из (4.14)
результат совпадает с химическим
потенциалом (2.62а) классического газа.
Из (4.14)
![]() ,
,
 (4.18)
(4.18)
получаем условия применимости классического распределения:
– масса частицы m – большая;
– концентрация частиц n – мала;
– температура T – велика.
Вырожденный газ фермионов проявляет квантовые свойства и нарушает условия (4.18), тогда
![]() ,
,
![]() .
.
Условия применимости квантового распределения:
– масса частицы мала;
– концентрация частиц велика;
– температура
не превышает критического значения
![]() ;
;
– ширина переходной области мала по сравнению с энергией Ферми;
– тепловая энергия возбуждает незначительное количество из общего числа частиц.
Критическая температура фермионов определяется условием
![]() .
.
Из (4.16) получаем
 .
.
Интеграл
равен
![]() ,
тогда
,
тогда
 .
(4.19)
.
(4.19)
Для
электронов
![]() ,
,
 .
.
При
![]() наиболее вероятная скорость
наиболее вероятная скорость
![]() соответствует длине волны де Бройля
соответствует длине волны де Бройля
 .
.
Концентрация выражается через среднее расстояние между электронами d
![]() .
.
Тогда из (4.19) получаем
![]() .
.
При критической температуре длина волны де Бройля сравнима со средним расстоянием между частицами.
Для квантового газа
![]() .
.
Для
классического газа
![]() ,
ширина переходной области сопоставима
с максимальной энергией фермионов, все
электроны получают тепловое возбуждение,
наиболее вероятный импульс большой,
длина волны де Бройля мала
,
ширина переходной области сопоставима
с максимальной энергией фермионов, все
электроны получают тепловое возбуждение,
наиболее вероятный импульс большой,
длина волны де Бройля мала
![]() .
.
Для электронного газа в металле
n
(1…18)1022
см–3,
m
10–27
г,
![]() .
.
При
нормальной температуре получаем
![]() ,
газ вырожден, доля возбужденных электронов
не превышает 1 %. Это объясняет противоречие
между классической теорией теплоемкости
и экспериментом, показавшим, что
электронный газ не дает вклада в
теплоемкость металла.
,
газ вырожден, доля возбужденных электронов
не превышает 1 %. Это объясняет противоречие
между классической теорией теплоемкости
и экспериментом, показавшим, что
электронный газ не дает вклада в
теплоемкость металла.
Для собственного полупроводника
n
1017
см–3,
![]() .
.
При
нормальной температуре
![]() ,
газ не вырожден, выполняется распределение
Максвелла.
,
газ не вырожден, выполняется распределение
Максвелла.
Молекулярный газ, например гелий с m » 3700 mэл, остается невырожденным до очень низких температур.
Тепловые флуктуации числа частиц. Из (4.5) и (4.6) для идеального газа бозонов, фермионов и классических частиц находим
 ,
,
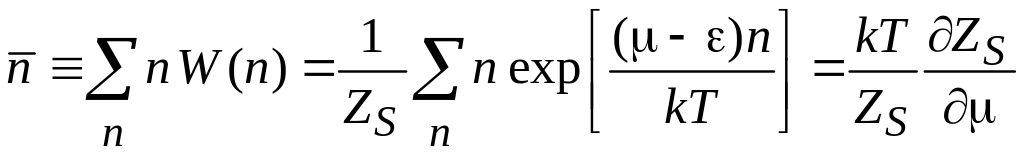 ,
,
 .
.
Тогда дисперсия числа частиц
 .
.
Для распределения (4.13)

получаем
 ,
,
тогда
![]() .
(4.20)
.
(4.20)
Для
фермионов
![]() ,
,
![]() .
.
При
![]() 0
и
1
получаем
0
и
1
получаем
![]() ,
на уровне Ферми
,
на уровне Ферми
![]() и
Dmax
= 0,25. Флуктуация
фермионов не велика и максимальна на
уровне Ферми.
и
Dmax
= 0,25. Флуктуация
фермионов не велика и максимальна на
уровне Ферми.
Для
бозонов
![]() ,
,
![]() .
.
При
большой заселенности уровня
![]() дисперсия
велика
дисперсия
велика
![]() .
.
Это объясняется взаимной интерференцией волновых пакетов, представляющих отдельные частицы и следующих в случайной последовательности. При интерференции двух волн с равными амплитудами наибольшая амплитуда удваивается, а интенсивность волны и плотность вероятности учетверяются. Наименьшая амплитуда и плотность вероятности равны нулю. В результате дисперсия числа частиц увеличивается. Интерференцией объясняется взаимное «притяжение» бозонов – при тепловом равновесии бозоны перемещаются группами. Например, фотонные пары с меньшим временным интервалом регистрируются чаще, чем пары с большим интервалом. Вероятность найти тождественные бозоны в близких квантовых состояниях выше, чем вероятность найти нетождественные частицы.
У фермионов перекрытие когерентных пакетов запрещено принципом Паули. Это приводит к взаимному «отталкиванию» фермионов и уменьшает флуктуацию числа частиц.
Корпускулярно-волновой дуализм бозонов. Из теории вероятности известно, что дисперсия аддитивна, если обусловлена независимыми причинами. Для бозонов
![]() .
.
Линейное
слагаемое соответствует классическим
частицам, флуктуация является дробовым
шумом. Квадратичное слагаемое соответствует
интерферирующим волнам, флуктуация
является волновым шумом. Наличие двух
вкладов в дисперсию фотонов обнаружил
А. Эйнштейн в 1909 г. Он рассматривал этот
факт как проявление корпускулярно-волнового
дуализма, т. е. совмещения волновых и
корпускулярных свойств. При малой
энергии, низкой частоте, большой длине
волны заселенность состояний бозонов
велика
,
тогда
![]() и система проявляет волновые свойства.
При большой энергии, большой частоте,
малой длине волны заселенность мала
и система проявляет волновые свойства.
При большой энергии, большой частоте,
малой длине волны заселенность мала
![]() ,
тогда
,
тогда
![]() и система проявляет корпускулярные
свойства. Для
классического идеального газа
,
дисперсия мала
и система проявляет корпускулярные
свойства. Для
классического идеального газа
,
дисперсия мала
![]() .
Флуктуация
является дробовым шумом,
газ ведет себя как множество частиц.
.
Флуктуация
является дробовым шумом,
газ ведет себя как множество частиц.
