
Примеры
9.1. Для идеального газа N двухатомных молекул, каждая из которых является линейным гармоническим осциллятором с частотой , найти колебательную статистическую сумму, внутреннюю энергию и теплоемкость при температуре T.
Уровни энергии линейного гармонического осциллятора
![]() ,
,
![]() ,
,
где
![]() Из (3.15) получаем
Из (3.15) получаем
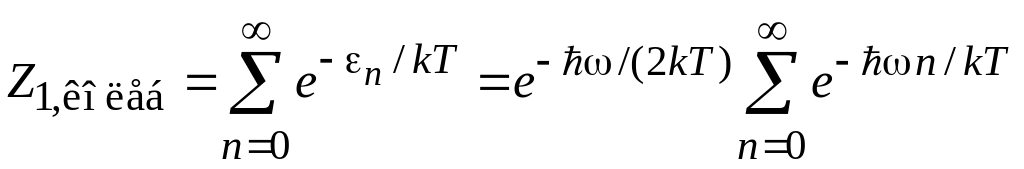 .
.
Суммируя геометрическую прогрессию, находим
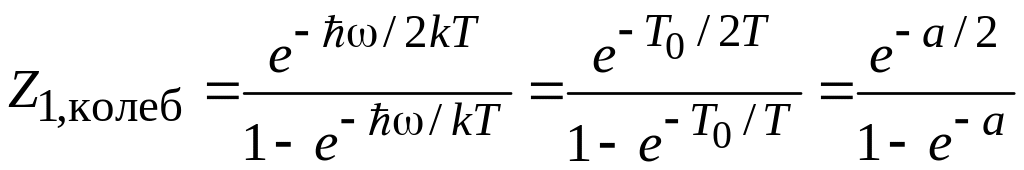 ,
,
![]() ,
(П.9.1)
,
(П.9.1)
где эффективная температура колебаний T0 и относительная температура:
![]() ,
,
![]() .
.
Например:
![]() ,
,
![]() ,
,
![]() .
Учитывая
.
Учитывая
![]()
и (3.17б), находим внутреннюю энергию, связанную с одной молекулой:
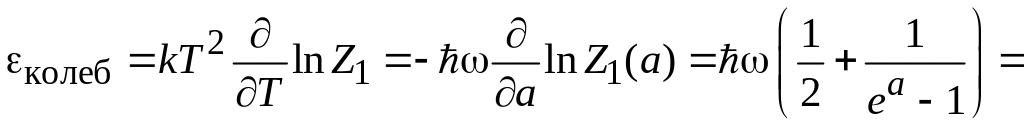
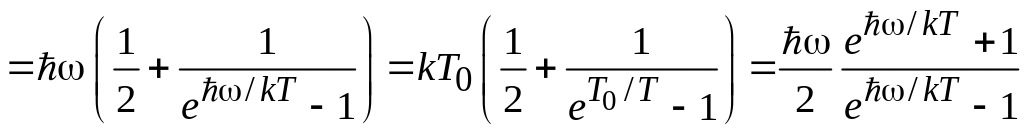 .
(П.9.2)
.
(П.9.2)
Сравнивая результат с энергией уровня n, получаем номер уровня с энергией, равной средней энергии осциллятора при температуре Т:
 .
(П.9.2а)
.
(П.9.2а)
Уровни
эквидистантные с шагом
![]() ,
поэтому
,
поэтому
![]() есть среднее
число квантов энергии
.
есть среднее
число квантов энергии
.
Теплоемкость системы N частиц равна
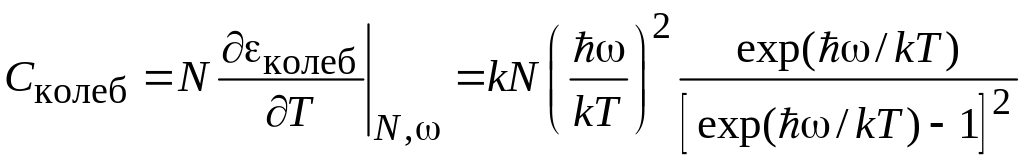 .
.
При
высоких температурах
![]() экспоненту (П.9.2) разлагаем в ряд и
сохраняем первые слагаемые
экспоненту (П.9.2) разлагаем в ряд и
сохраняем первые слагаемые
![]() ,
тогда
,
тогда
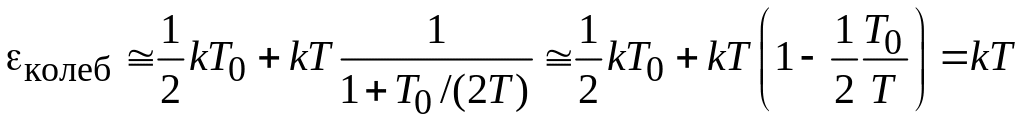 .
.
Учитывая результат классического решения в примере 3.3, получаем, что при высоких температурах колебательная теплоемкость
![]()
не зависит от температуры и квантовая статистика переходит в классическую, что подтверждает условие (3.2) применимости классического описания.
При
низких температурах
![]() ,
,
![]() колебательная теплоемкость стремится
к нулю по закону
колебательная теплоемкость стремится
к нулю по закону
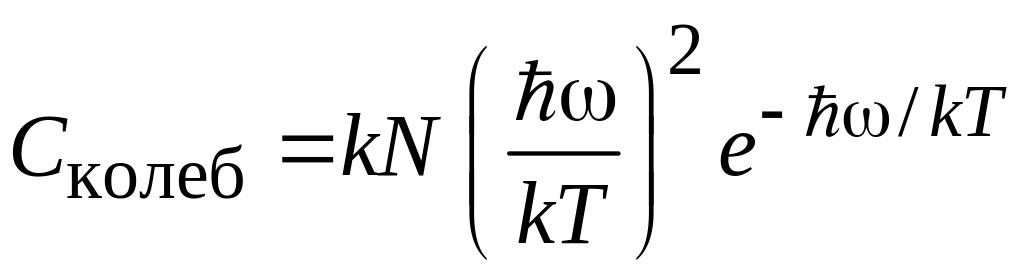 .
.
Это
противоречит теореме классической
физики о равном распределении энергии
по степеням свободы и подтверждает
третье
начало термодинамики,
согласно которому теплоемкость обращается
в нуль при
![]() .
.
N независимых частиц со спином и с магнитным моментом находятся в магнитном поле В и занимают объем V при температуре T. Найти среднюю энергию, среднюю проекцию магнитного момента и критическую температуру спонтанной намагниченности.
Проекциям
спина на направление магнитного поля,
показанным на рис. 3.10, соответствуют
энергии
![]() и
и
![]() .
Используя (3.15), находим статистическую
сумму частицы
.
Используя (3.15), находим статистическую
сумму частицы
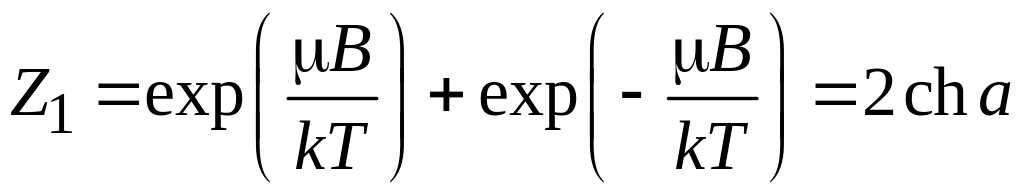 ,
(П.9.11)
,
(П.9.11)
где
![]() .
Из (3.14б) получаем вероятности состояний,
среднюю энергию и среднюю проекцию
магнитного момента частицы
.
Из (3.14б) получаем вероятности состояний,
среднюю энергию и среднюю проекцию
магнитного момента частицы
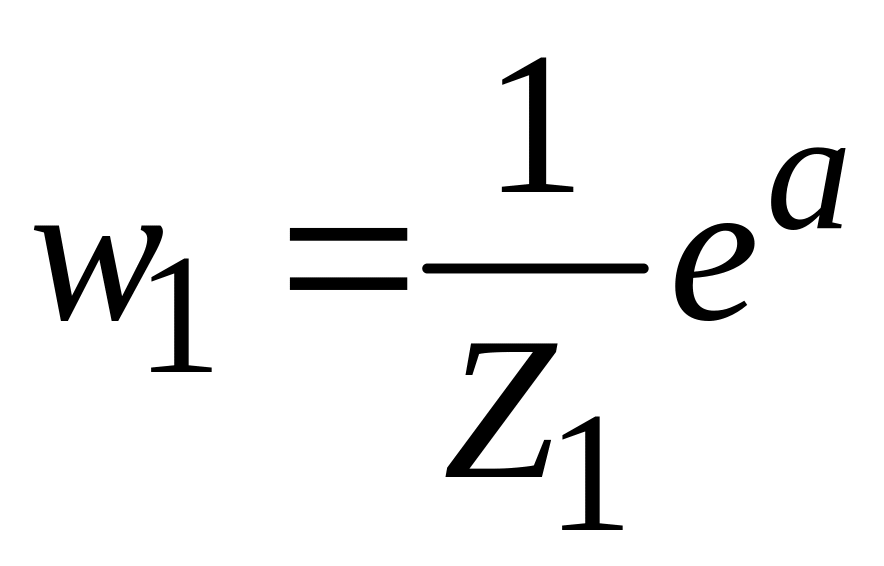 ,
,
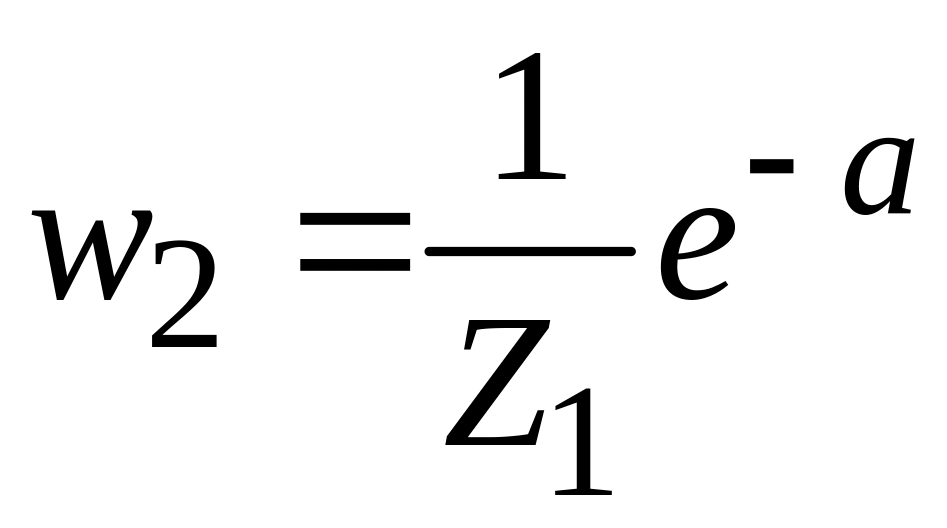 ,
,
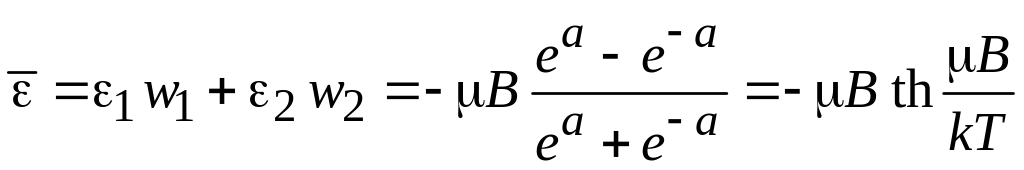 ,
(П.9.12)
,
(П.9.12)
![]() .
(П.9.13)
.
(П.9.13)
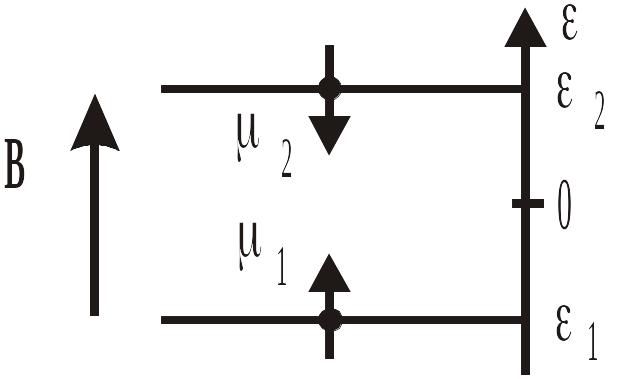
Рис. 3.10. Энергии магнитных моментов
В
слабом поле
![]() ,
и из (П.9.13) получаем магнитный момент
системы N
частиц
,
и из (П.9.13) получаем магнитный момент
системы N
частиц
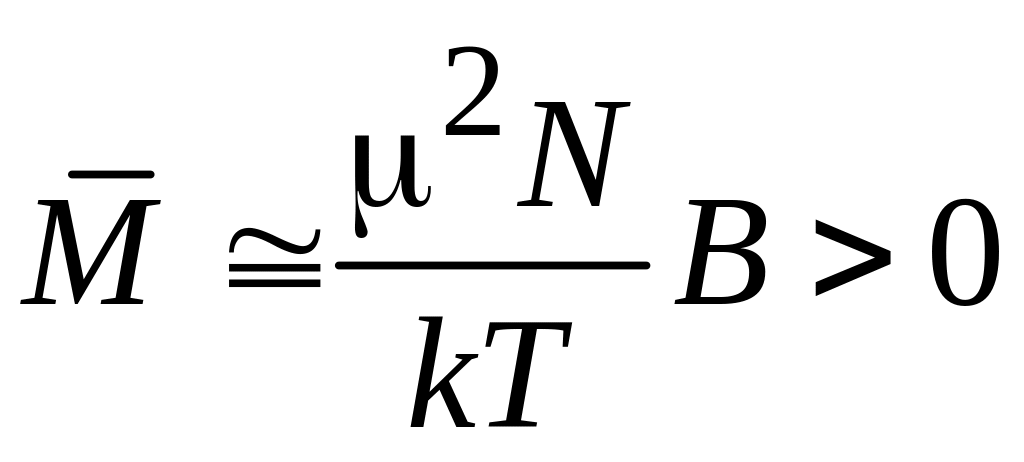 .
.
Следовательно,
система со
спином
1/2 проявляет
парамагнитные свойства.
Это установил Вольфганг Паули в 1926 г.
Результаты
![]() ,
,
![]() являются следствием
являются следствием
![]() .
В классическом пределе при
.
В классическом пределе при
![]() получаем
получаем
![]() ,
что следует из теоремы
Бора – Ван-Левен.
,
что следует из теоремы
Бора – Ван-Левен.
Если при изменении поля сохранять заселенности уровней, т. е. среднюю проекцию магнитного момента, то из (П.9.13) получаем
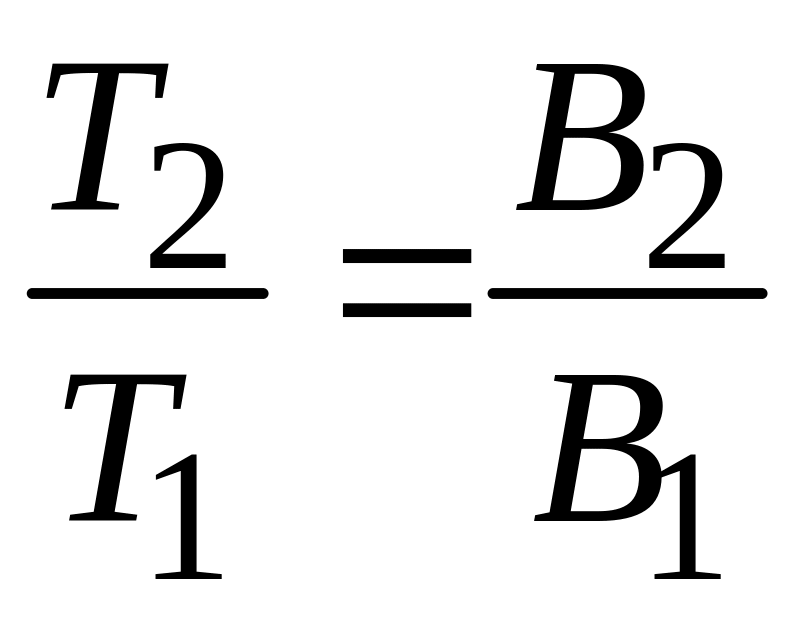 .
(П.9.13а)
.
(П.9.13а)
Следовательно, адиабатическое уменьшение магнитного поля охлаждает систему. Метод магнитного охлаждения на основе парамагнитных солей предложили Петер Дебай и Уильям Джиок в 1926 г. Метод применяется для получения температур от 0,3 до 510–3 К.
Магнитный момент единицы объема, т. е. намагниченность системы во внешнем поле согласно (П.9.13) равна
![]()
![]() ,
(П.9.13б)
,
(П.9.13б)
тогда магнитная восприимчивость
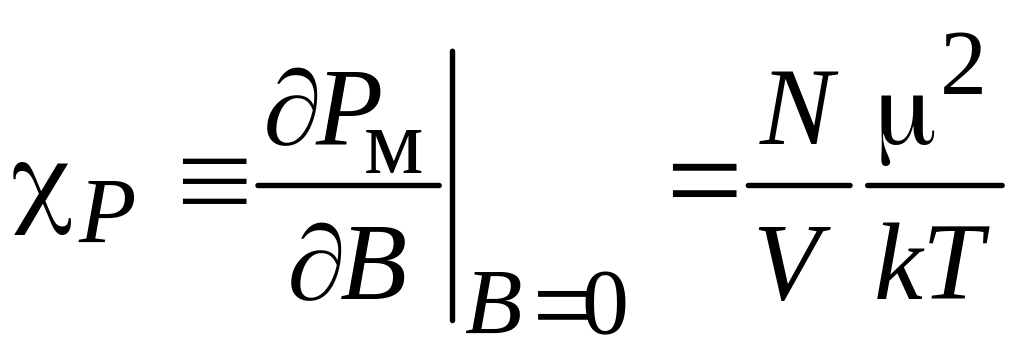 .
.
Намагниченность создает собственное магнитное поле системы
![]() .
.
Для
объяснения спонтанной намагниченности
ферромагнетика Борис Львович Розинг в
1892 г. и Пьер Вейсс в 1907 г. предложили
добавлять в (П.9.13б) возникающее поле к
внешнему полю
![]() ,
тогда
,
тогда
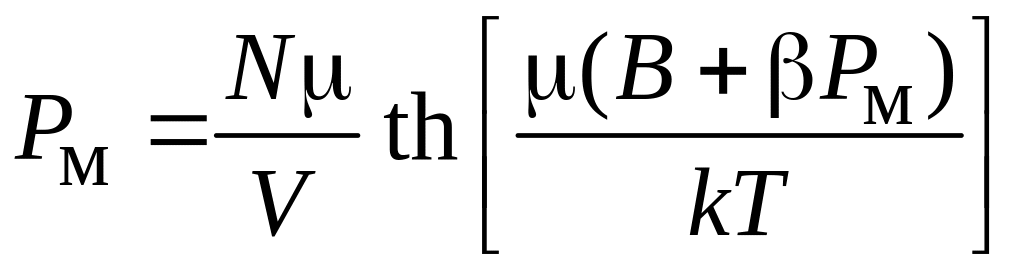 .
.
При выключенном внешнем поле получаем
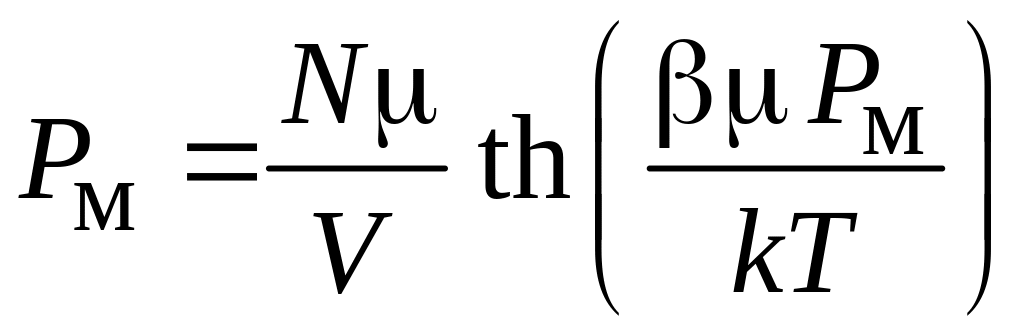 .
.
Замена
![]() дает уравнение
дает уравнение
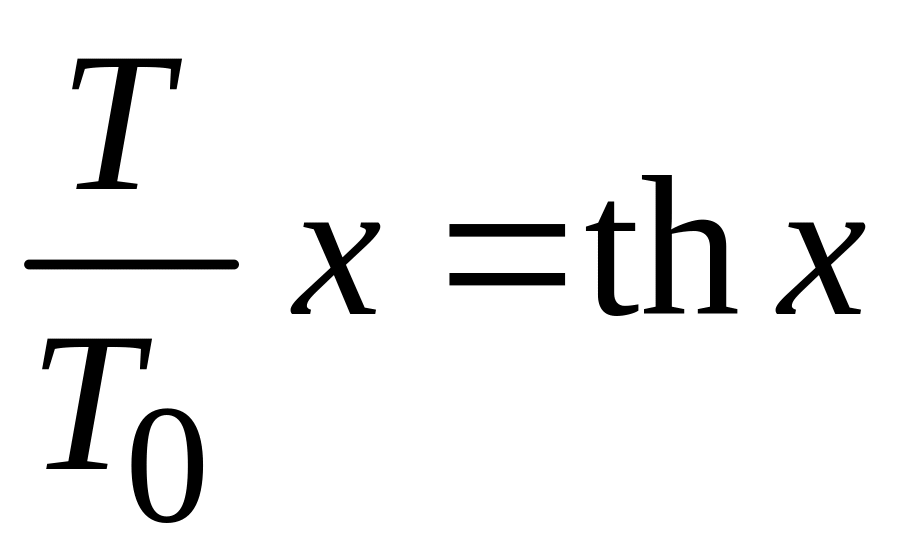 ,
(П.9.14)
,
(П.9.14)
где введена критическая температура Кюри
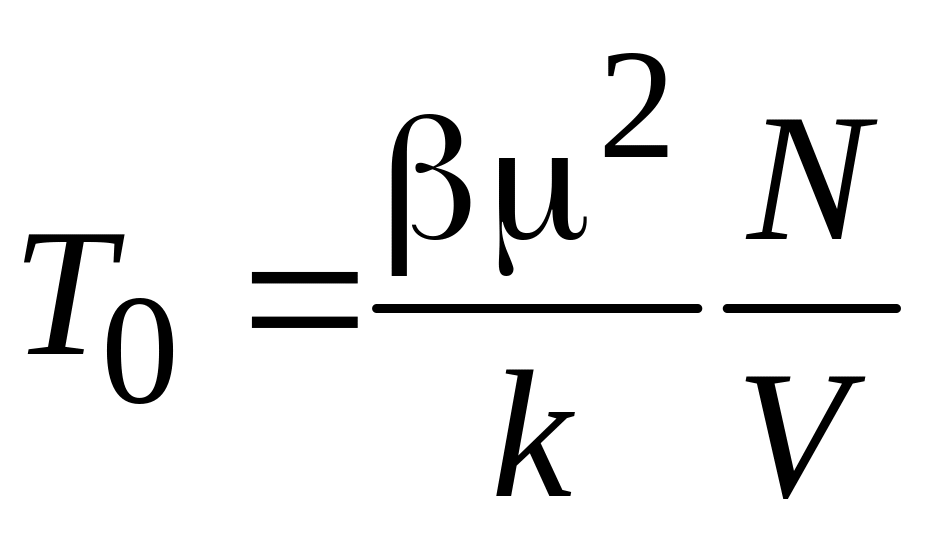 .
(П.9.15)
.
(П.9.15)
При
температуре выше критической
![]() равенство (П.9.14) нарушается при
равенство (П.9.14) нарушается при
![]() ,
тогда получаем решение
, следовательно,
спонтанная намагниченность не возникает.
При температуре ниже критической
,
тогда получаем решение
, следовательно,
спонтанная намагниченность не возникает.
При температуре ниже критической
![]() уравнение (П.9.14) имеет не равные нулю
решения. Происходит фазовый переход
второго рода, внутренняя симметрия
системы изменяется и появляется
ферромагнитное состояние в виде спонтанно
намагниченных областей – доменов.
Используя
уравнение (П.9.14) имеет не равные нулю
решения. Происходит фазовый переход
второго рода, внутренняя симметрия
системы изменяется и появляется
ферромагнитное состояние в виде спонтанно
намагниченных областей – доменов.
Используя
![]() ,
из (П.9.14) получаем
,
из (П.9.14) получаем
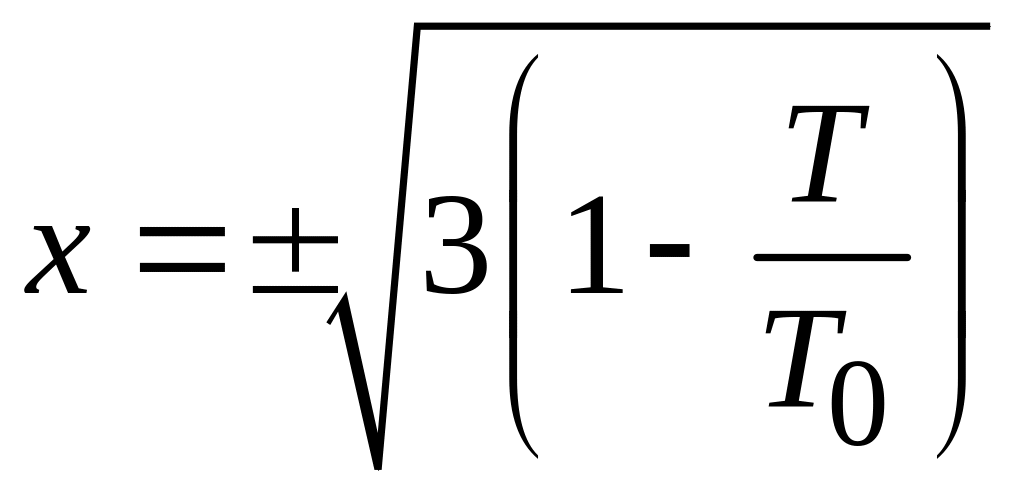 .
.
Спонтанная намагниченность
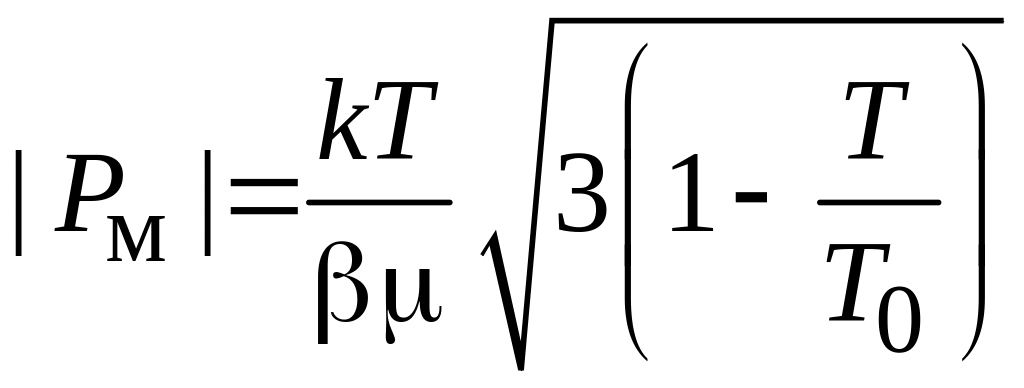 (П.9.16)
(П.9.16)
достигает
максимума при
![]() .
Сравнение (П.9.15) и (П.9.16) с экспериментом,
дает
.
Сравнение (П.9.15) и (П.9.16) с экспериментом,
дает
![]() .
Столь сильное взаимодействие магнитных
моментов не может создать магнитное
поле. Яков Ильич Френкель и независимо
Вернер Гейзенберг показали в 1928 г., что
электростатическое взаимодействие
между электронами атомов сопровождается
квантовым обменным взаимодействием,
существенно превышающим магнитное
взаимодействие, и этим объясняется
спонтанная намагниченность ферромагнетика.
.
Столь сильное взаимодействие магнитных
моментов не может создать магнитное
поле. Яков Ильич Френкель и независимо
Вернер Гейзенберг показали в 1928 г., что
электростатическое взаимодействие
между электронами атомов сопровождается
квантовым обменным взаимодействием,
существенно превышающим магнитное
взаимодействие, и этим объясняется
спонтанная намагниченность ферромагнетика.
