Каноническое распределение квантового идеального газа
Идеальный газ с фиксированным числом частиц, объемом и температурой описывается каноническим распределением. Оно дает вероятность определенного значения энергии. Для квантовой системы учитываем:
дискретность спектра энергии пространственно ограниченной системы;
вырождение состояний по энергии;
тождественность микрочастиц;
принцип запрета Паули для фермионов.
Квантовое распределение получается из классического на основе правила соответствия – соотношения между динамическими характеристиками одинаковы в классической и квантовой теориях.
Вероятность
состояния системы.
Из канонического
распределения (2.17) для классической
системы получаем вероятность
невырожденного
состояния
квантовой системы с полной энергией
.
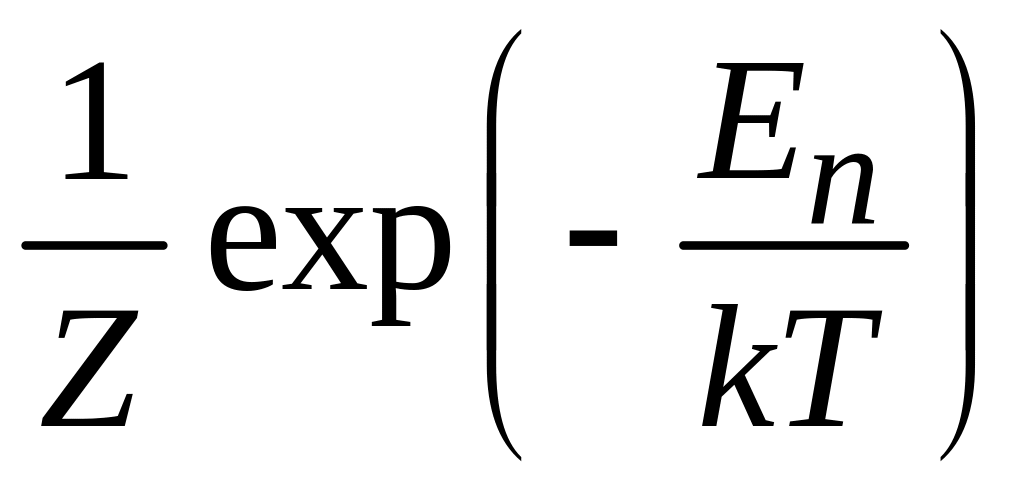Кратность
вырождения системы
равна числу
отличающихся по квантовым числам
состояний, имеющих одинаковую энергию
.
Вероятность каждого состояния
.
Эти состояния несовместимы – реализуется
или первое состояние, или второе и так
далее вплоть до состояния
.
Вероятность сложного состояния в
раз больше, тогда система имеет энергию
с вероятностью
,
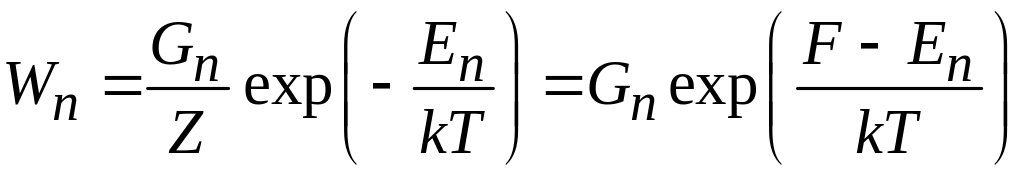(3.12)
где свободная энергия
.
Статистическая сумма системы Z. Из условия нормировки
находим
.
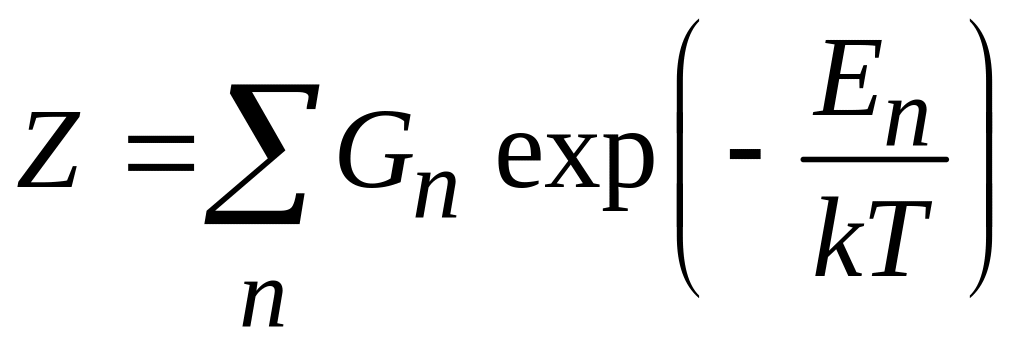(3.13)
Термодинамические величины являются средними по статистическому ансамблю. Внутренняя энергия
.
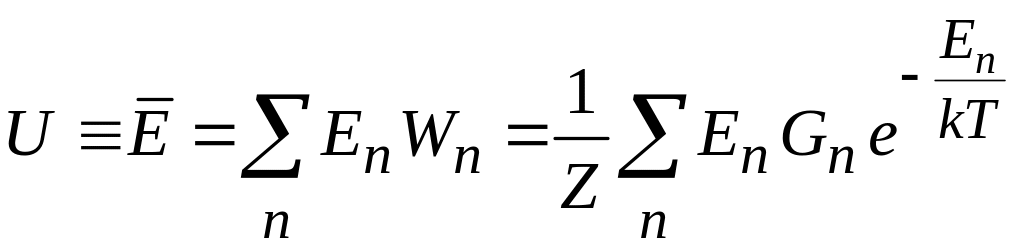Из (3.13) находим
.
(3.13а)
Аналогично (2.35) получаем энтропию
.
(3.13б)
Вероятность и статистическая сумма для одной частицы. Частицы идеального газа независимы друг от друга, вид канонического распределения не зависит от числа частиц. Применяя (3.12) к одной частице системы, когда остальные частицы рассматриваются как термостат, получаем вероятность состояния i частицы
,
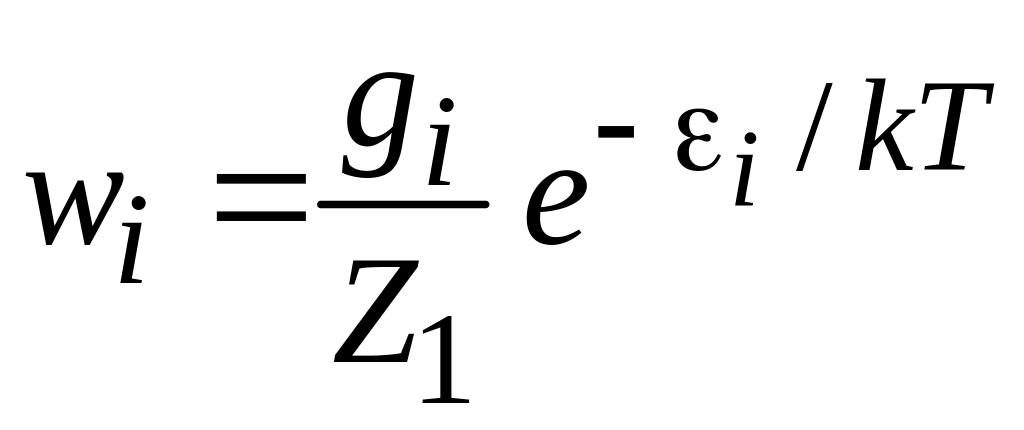(3.14)
где
и
– энергия и кратность вырождения
состояния i;
– статистическая сумма частицы. Ее
тепловое движение складывается из
независимых видов α:
поступательного, вращательного,
колебательного, изменения внутреннего
состояния. Полная энергия равна сумме
энергий этих движений
.
По теореме умножения вероятностей
,
(3.14а)
где аналогично (3.14)
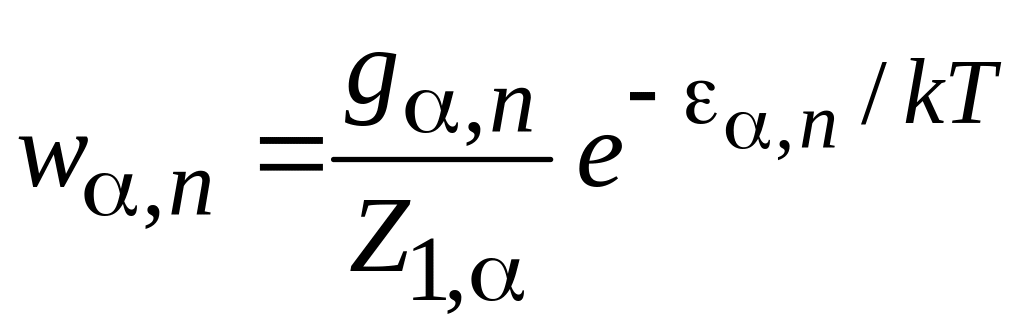(3.14б)
– вероятность
состояния n
с энергией
и кратностью вырождения
для вида движения α. Условие нормировки
для (3.14б) дает
.
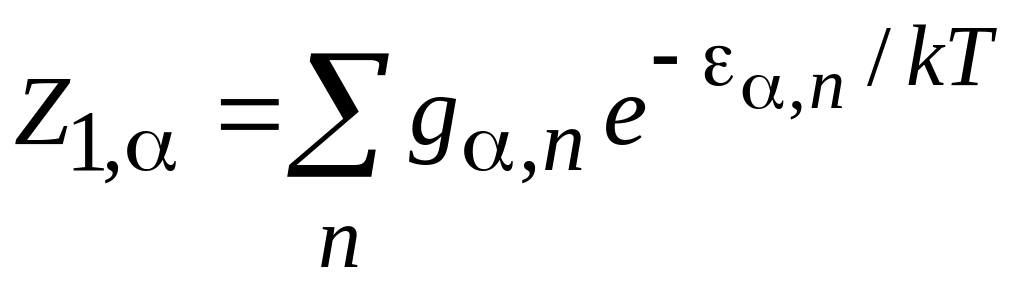(3.15)
Для
частицы идеального газа, находящегося
в макроскопическом объеме, спектр
поступательного движения квазинепрерывный.
Поэтому
не отличается, согласно правилу
соответствия, от классического выражения
(П.3.3)
.
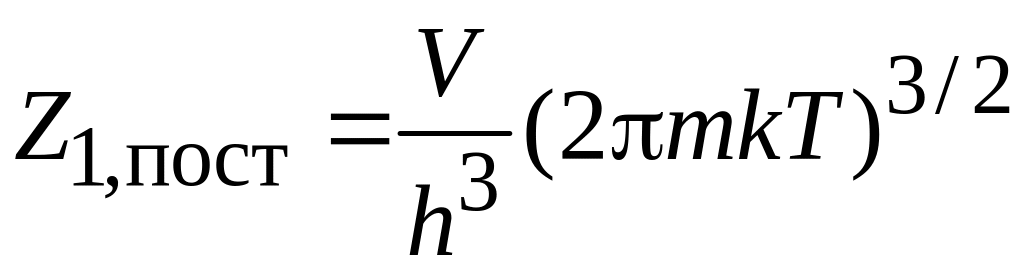(3.15а)
Для
молекулы с частотой собственных колебаний
и моментом инерции J
,
,
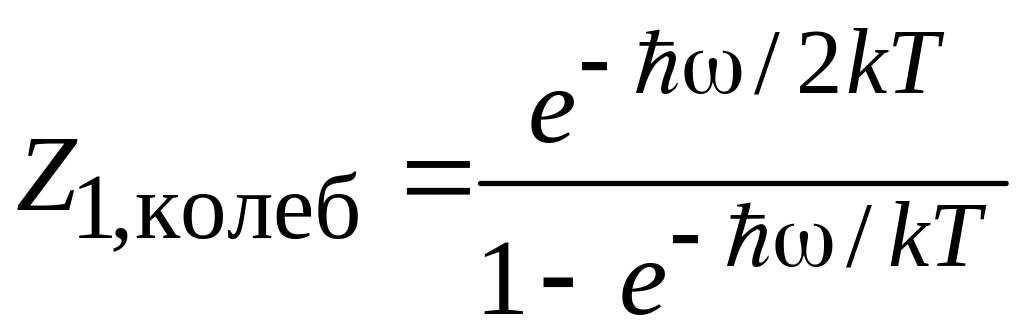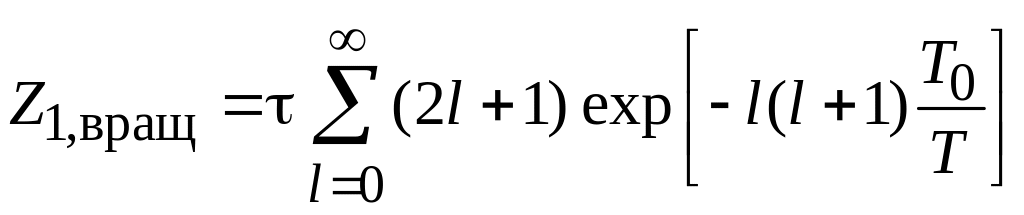(3.15б)
где
эффективная температура
.
Статистическая сумма идеального газа. Учитывая (3.14), (3.14а) и (3.14б), получаем
.
(3.16)
Для N одинаковых статистически независимых частиц энергия системы складывается из энергий частиц, а вероятность состояния системы равна произведению вероятностей состояний отдельных частиц. Экспоненциальная зависимость (3.12) и (3.14) дает
,
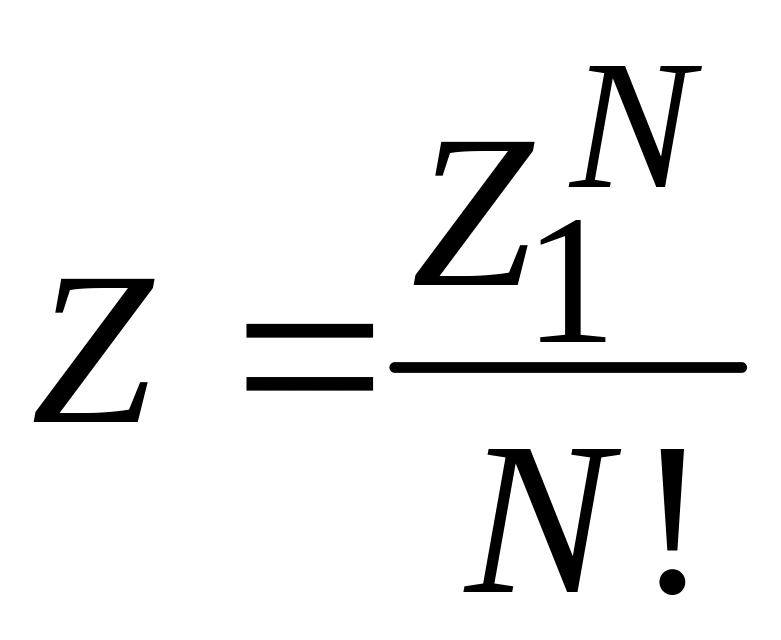(3.17)
где учтено, что N! состояний, отличающихся перестановкой тождественных частиц, физически не различимы и должны учитываться однократно. Учитывая (3.16), из (3.17) получаем
.
(3.17а)
Внутренняя энергия идеального газа связана со средней энергией частицы
.
Используя (3.13а) и (3.17), находим
.
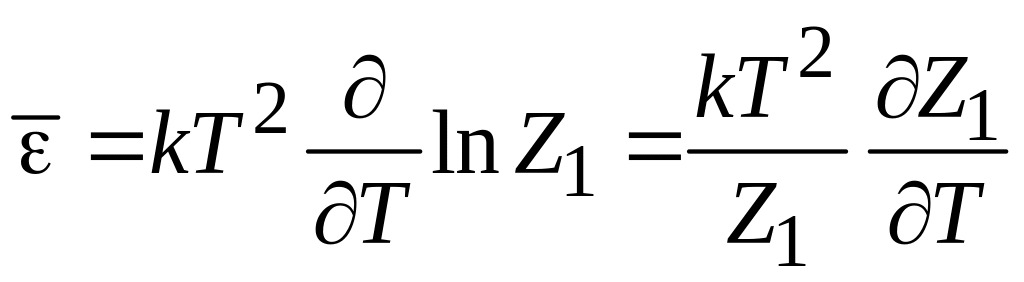(3.17б)