Квантовая статистическая физика

Квантовая статистическая физика изучает системы из большого числа частиц, подчиняющихся законам квантовой механики, из которых следует:

• дискретность спектра энергии пространственно ограниченной системы;

• вырождение состояний по энергии;

• тождественность микрочастиц;

• принцип запрета Паули для фермионов.

Рассмотрим условия, которые делают необходимым учет этих свойств.

Условия применимости классической и квантовой статистической физики

На рубеже XIX–XX вв. делались попытки применить классическую статистическую физику для описания электромагнитного теплового излучения в полости и электронного газа в металле. Оказалось, что ее следствия противоречат опыту. Например, теплоемкость металла складывается из теплоемкости ионной решетки и теплоемкости электронов проводимости , тогда . Число степеней свободы электрона равно трем и из теоремы о распределении энергии по степеням свободы следует молярная теплоемкость . Ион решетки имеет три колебательные степени свободы, на каждую приходится энергия kT, тогда . В результате из классической теории следует молярная теплоемкость металла и молярная теплоемкость диэлектрика . Измерения, выполненные при нормальной и более высокой температурах, подтвердили закон Дюлонга и Пти (П.4.3)

как для металлов, так и для диэлектриков. Следовательно, электронный газ не дает вклада в теплоемкость металла. При температуре, существенно меньшей нормальной, измеренная теплоемкость диэлектриков

,

для металлов

.

Объяснить эти результаты классическая теория не в состоянии, здесь необходимо учитывать квантовые свойства микрочастиц.

Условия применимости классического описания

1. Высокие температуры, при которых несущественна дискретность квантовых состояний:

,

где и – уровни энергии системы.

Если электрон находится в кубическом ящике со стороной L, то из краевого условия Борна–Кармана получаем

,

где n_x – целое. Откуда находим

,

.

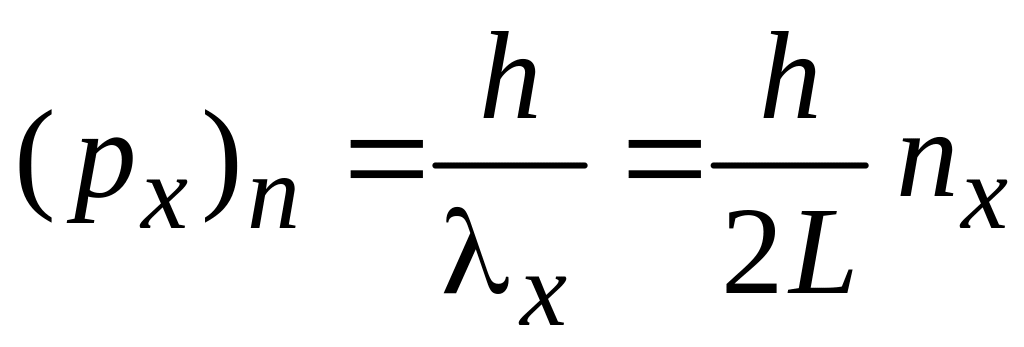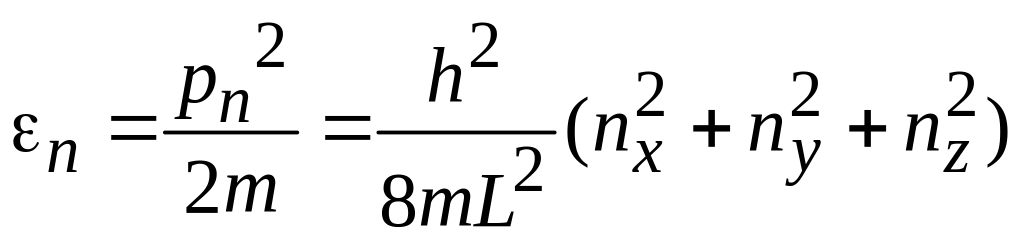Для L = 1 мм получаем , что соответствует тепловой энергии kT с температурой порядка 10^–9 К. Для частицы, находящейся в макроскопическом объеме, квантование энергии поступательного движения несущественно при больших значениях квантовых чисел и высоких температурах.

2. Большое значение параметра r системы с размерностью длины по сравнению с длиной волны де Бройля

.

Для идеального газа наиболее вероятный импульс частицы соответствует

.

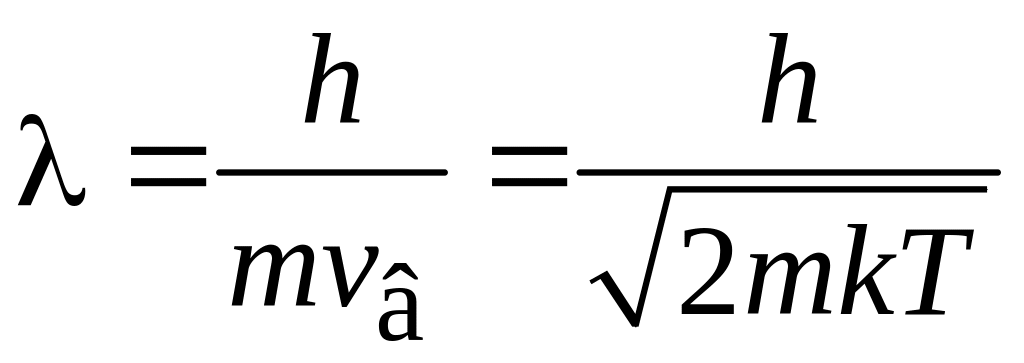Для среднего расстояния между частицами получаем , тогда

,

где n – концентрация молекул. Условие принимает вид

. (3.1)

Классическая теория идеального газа выполняется при достаточно малых концентрациях, высоких температурах и не слишком малых массах частиц. Сопоставляя (3.1) с выражением для химического потенциала (2.62а), получаем

 < 0.

В области применимости классической теории химический потенциал отрицателен.

Для гелия при нормальных условиях

, ,

, .

Выполняется и классическая физика применима.

Для электронов в металле при нормальной температуре 10^–7 см, расстояние между узлами кристаллической решетки  0,210^–7см. Условие нарушается и классическая физика не применима для электронного газа в металле.

3. Большой объем фазового пространства, приходящийся на одну частицу:

.

Для кристаллической решетки средняя кинетическая энергия узла равна

,

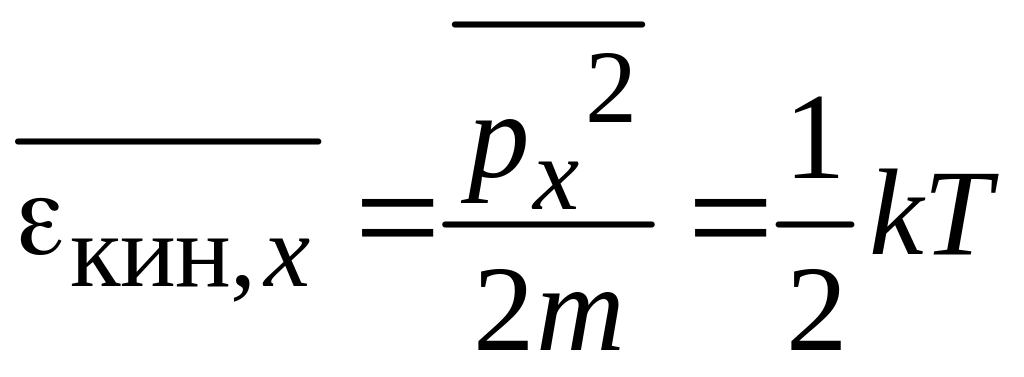тогда флуктуация

.

Потенциальная энергия упругих колебаний

,

.

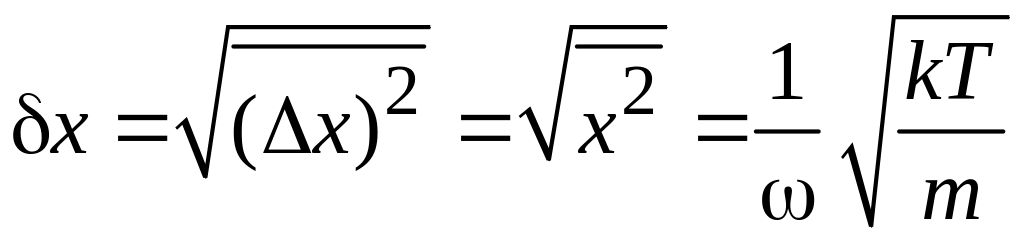В результате

,

. (3.2)

Чем прочнее кристалл, тем больше частота  собственных колебаний узлов решетки – для меди , для алмаза . В результате чем прочнее кристалл и ниже температура, тем меньше согласие с классической теорией.

Для описания систем, которые нарушают хотя бы одно полученное условие, необходимо использовать квантовую статистическую физику.