
Уровни Ландау
Состояния заряда в однородном магнитном поле получил Л.Д. Ландау в 1930 г.
Гамильтониан (5.40)
 .
.
В
декартовых координатах для поля
![]() ,
с учетом
,
в частности
,
с учетом
,
в частности
 ,
используем
,
используем
![]() ,
,
тогда
 .
(5.46)
.
(5.46)
Уравнение Шредингера получает вид

 .
.
Операторы
![]() и
и
![]() коммутируют с
коммутируют с
![]() ,
тогда решение содержит произведение
собственных функций
и
,
тогда решение содержит произведение
собственных функций
и
 ,
,
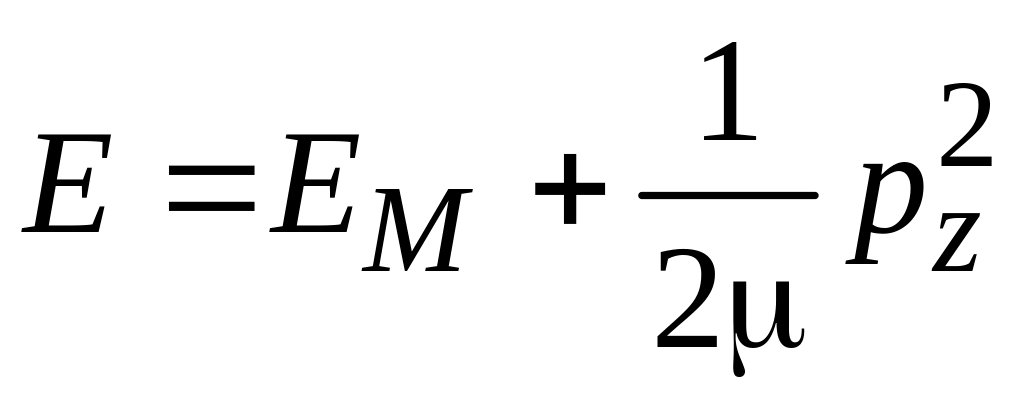 .
.
Если
движение по оси z
не ограниченное, то
![]() – любое вещественное число. Подстановка
решения в уравнение и деление его слева
на ψ дает уравнение для
– любое вещественное число. Подстановка
решения в уравнение и деление его слева
на ψ дает уравнение для
![]()

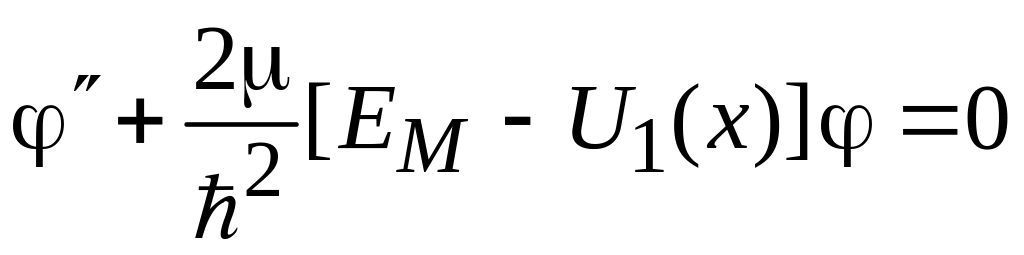 ,
,
где
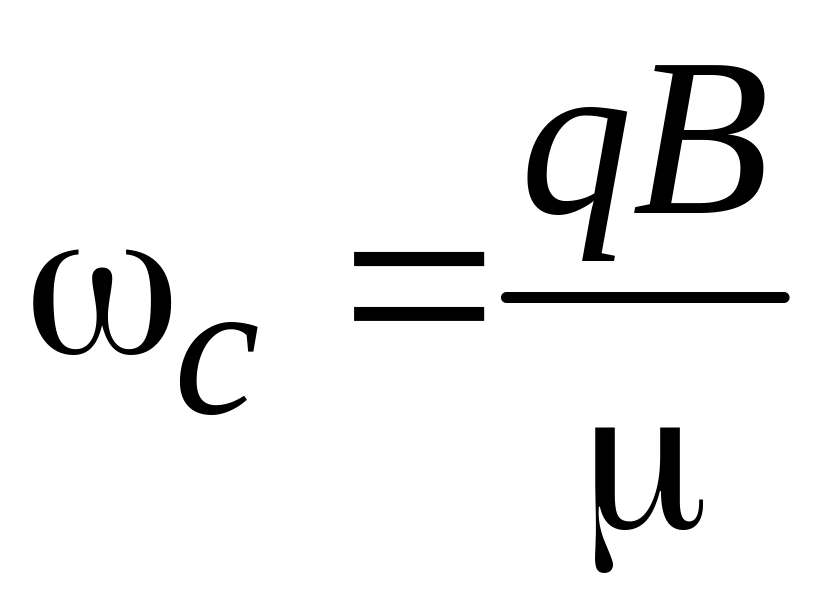 – циклотронная частота (1.23). Эффективная
потенциальная энергия
– циклотронная частота (1.23). Эффективная
потенциальная энергия
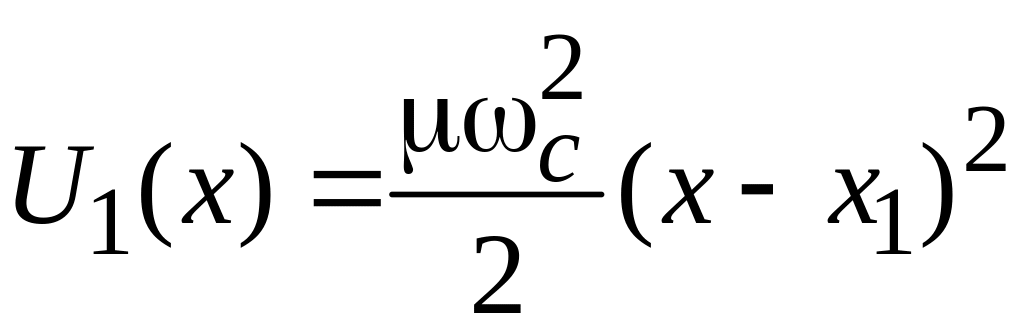
соответствует потенциальной энергии гармонического осциллятора (3.23), колеблющегося около точки:
 (5.47)
(5.47)
с
частотой
![]() и с амплитудой (3.40) нулевых колебаний
и с амплитудой (3.40) нулевых колебаний
![]() ,
где
,
где
![]() – магнитная длина. Из (3.32) получаем
– магнитная длина. Из (3.32) получаем
 ,
,
![]()
Уровни
Ландау.
Спектр энергии движения в плоскости
![]() совпадает со спектром гармонического
осциллятора. Из (3.39) находим
совпадает со спектром гармонического
осциллятора. Из (3.39) находим
 .
(5.48)
.
(5.48)
Число
состояний на уровне Ландау.
Состояние
![]() зависит от положения центра циклотронного
движения
зависит от положения центра циклотронного
движения
![]() ,
энергия (5.48) не зависит от
,
поэтому уровень Ландау вырожден. Для
движения в области
,
энергия (5.48) не зависит от
,
поэтому уровень Ландау вырожден. Для
движения в области
![]() ,
,
 условие
условие
![]() на центр (5.47) ограничивает импульс
на центр (5.47) ограничивает импульс
![]() интервалом
интервалом
![]() .
Пространственное ограничение по оси y
вызывает квантование
.
Пространственное ограничение по оси y
вызывает квантование
![]() .
Граничное условие Борна–Кармана (3.8)
требует
.
Граничное условие Борна–Кармана (3.8)
требует
 ,
,
![]() ,
,
 ,
,
где
N
– целое число. Допустимые значения
импульса имеют шаг
![]() .
Учитывая степень вырождения σ состояний
по спину и (1.32)
.
Учитывая степень вырождения σ состояний
по спину и (1.32)
![]() ,
находим кратность вырождения уровня n
,
находим кратность вырождения уровня n
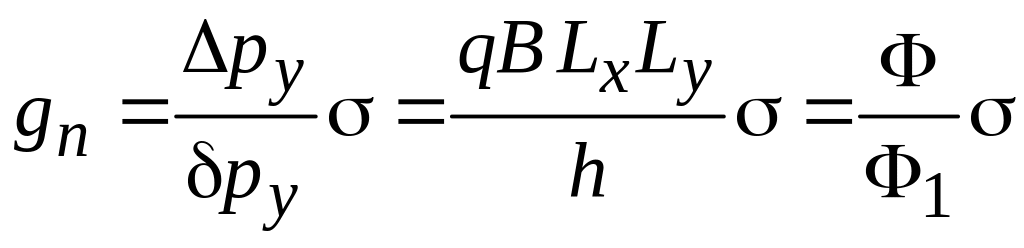 .
(5.52)
.
(5.52)
Число состояний на уровне Ландау пропорционально числу квантов магнитного потока, приходящихся на область, доступную для движения заряда.
Эффект Ааронова–Бома
Магнитное и электрическое поля выражаются через потенциалы
![]() ,
,
![]() .
.
В
классической электродинамике векторный
потенциал
![]() ,
не зависящий от времени, и скалярный
потенциал
,
не зависящий от времени, и скалярный
потенциал
![]() ,
не зависящий от координат, не действуют
на заряд. Д. Бом и Я. Ааронов показали в
1959 г., что фаза
волновой функции изменяется под действием
скалярного и векторного потенциалов,
даже в том случае, когда нет силового
действия поля на частицу.
Эффект Аронова–Бома подтвержден
интерференционными экспериментами и
свидетельствует о нелокальности
квантового состояния.
,
не зависящий от координат, не действуют
на заряд. Д. Бом и Я. Ааронов показали в
1959 г., что фаза
волновой функции изменяется под действием
скалярного и векторного потенциалов,
даже в том случае, когда нет силового
действия поля на частицу.
Эффект Аронова–Бома подтвержден
интерференционными экспериментами и
свидетельствует о нелокальности
квантового состояния.
Магнитный
эффект. Пусть
заряд q
движется перпендикулярно магнитному
полю В
по замкнутой траектории. Полуклассическое
квантование (1.22)
 ,
с учетом
,
с учетом
![]() дает
дает
 ,
(5.53)
,
(5.53)
где
![]() – магнитный поток через поверхность,
ограниченную траекторией
– магнитный поток через поверхность,
ограниченную траекторией
![]() Изменение фазы при прохождении частицей
траектории n
без магнитного поля
Изменение фазы при прохождении частицей
траектории n
без магнитного поля
 .
.
Вклад магнитного поля в фазу при движении по замкнутой траектории
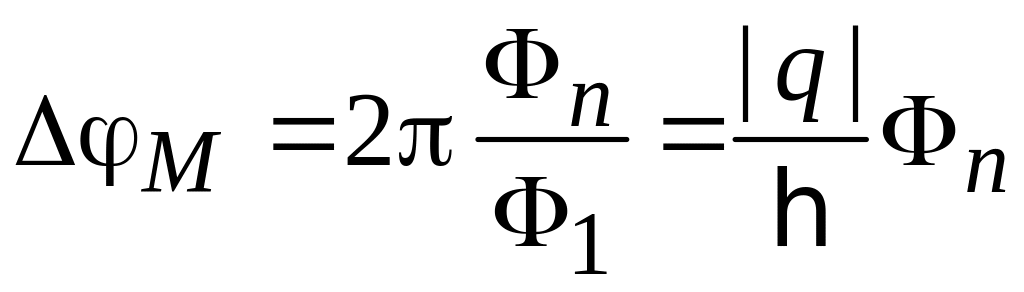 .
(5.54)
.
(5.54)
Для
незамкнутой траектории между точками
r0
и r
поток обобщается
 ,
тогда
,
тогда
 .
(5.55)
.
(5.55)
Векторный потенциал изменяет фазу волновой функции.
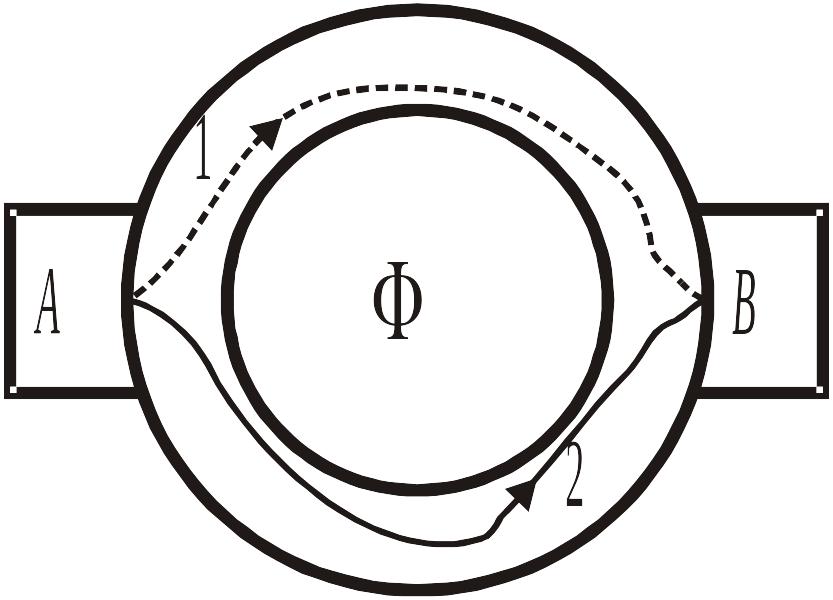
Осцилляции
сопротивления
проводящего кольца при изменении
магнитного потока исследовали Ю.В. и
Д.Ю. Шарвины в 1981 г. Кольцо из магния
диаметром (1,52)
мкм при температуре ~ 1К обеспечивает
длину когерентности электронов,
превышающую размер кольца. На платиновые
контакты А
и В
подается напряжение. Через кольцо
проходит магнитный поток Ф. Электронная
волна разделяется на контакте А,
идет по путям 1 и 2, набирая фазы φ1
и φ2,
и интерферирует на контакте В
с разностью фаз
![]() .
Учитывая, что при обращении движения
набираемая фаза меняет знак, из (5.54)
получаем
.
Учитывая, что при обращении движения
набираемая фаза меняет знак, из (5.54)
получаем
 .
.
Изменение
магнитного потока меняет разность фаз.
Максимум интерференции
![]() ,
где
,
соответствует максимуму тока между
контактами. В результате, при изменении
магнитного поля сопротивление между
контактами осциллирует с периодом
,
где
,
соответствует максимуму тока между
контактами. В результате, при изменении
магнитного поля сопротивление между
контактами осциллирует с периодом
![]() .
.
Если
через кольцо одновременно переносится
заряд
![]() ,
то период осцилляций равен
,
то период осцилляций равен
![]() .
.
Электрический
эффект. Фаза
волновой функции частицы с постоянной
полной энергией
![]() изменяется пропорционально времени
изменяется пропорционально времени
![]() .
Заряд q,
движущийся в
течение времени τ в
электрическое
поле с потенциалом
,
за счет потенциальной энергии
.
Заряд q,
движущийся в
течение времени τ в
электрическое
поле с потенциалом
,
за счет потенциальной энергии
![]() набирает дополнительную фазу
набирает дополнительную фазу
 .
(5.57)
.
(5.57)
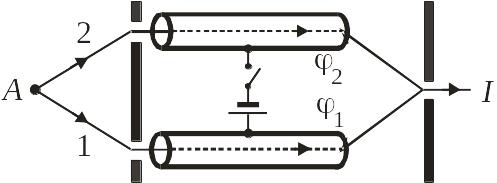
В
эксперименте электрон в виде волнового
пакета испускается в т. A,
проходит через отверстия экрана 1 и 2 и
движется внутри проводящих цилиндров,
экранирующих электрическое поле
![]() .
За время движения электрона внутри
цилиндров внешнее поле включается,
поддерживается постоянным и отключается.
На всех этапах движения силовое
воздействие на электрон отсутствует.
Согласно (5.57) на путях 1 и 2 набирается
разность фаз
.
За время движения электрона внутри
цилиндров внешнее поле включается,
поддерживается постоянным и отключается.
На всех этапах движения силовое
воздействие на электрон отсутствует.
Согласно (5.57) на путях 1 и 2 набирается
разность фаз
![]() ,
где
,
где
![]() – разность потенциалов цилиндров.
Максимальный интерференционный ток в
цепи соответствует
– разность потенциалов цилиндров.
Максимальный интерференционный ток в
цепи соответствует
![]() ,
где
,
где
![]() ,
тогда
,
тогда
![]() .
Следовательно, при изменении разности
потенциалов ток I
и сопротивление цепи осциллируют с
периодом
.
Следовательно, при изменении разности
потенциалов ток I
и сопротивление цепи осциллируют с
периодом
![]() .
(5.58)
.
(5.58)
Эффект Зеемана состоит в расщеплении уровней энергии атома в магнитном поле. Явление обнаружил Питер Зееман в 1896 г.
Для электрона в слабом однородном магнитном поле из (5.40) получаем
 ,
,
где
![]() ;
;
![]() – гамильтониан взаимодействия электрона
в атоме; отброшено малое слагаемое,
пропорциональное
– гамильтониан взаимодействия электрона
в атоме; отброшено малое слагаемое,
пропорциональное
![]() .
Используем калибровку векторного
потенциала
.
Используем калибровку векторного
потенциала
![]() ,
,
![]() ,
,
![]() ,
,
,
,
тогда
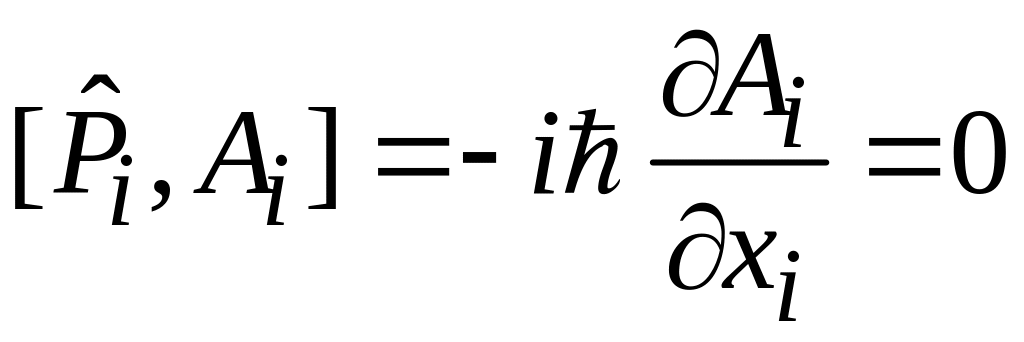 ,
,
![]() ,
,
![]() ,
,
где
![]() – оператор орбитального момента;
– оператор орбитального момента;
![]() .
В результате
.
В результате
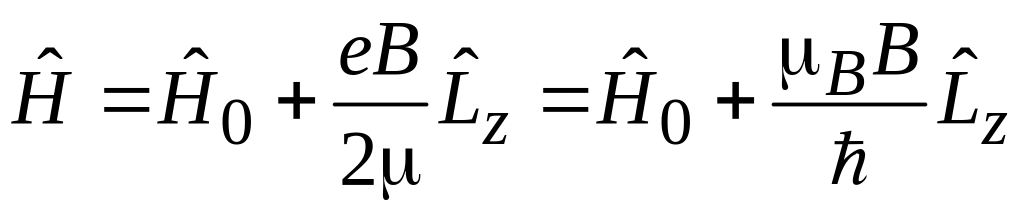 ,
,
где
![]() – гамильтониан электрона в атоме без
учета магнитного поля;
– гамильтониан электрона в атоме без
учета магнитного поля;
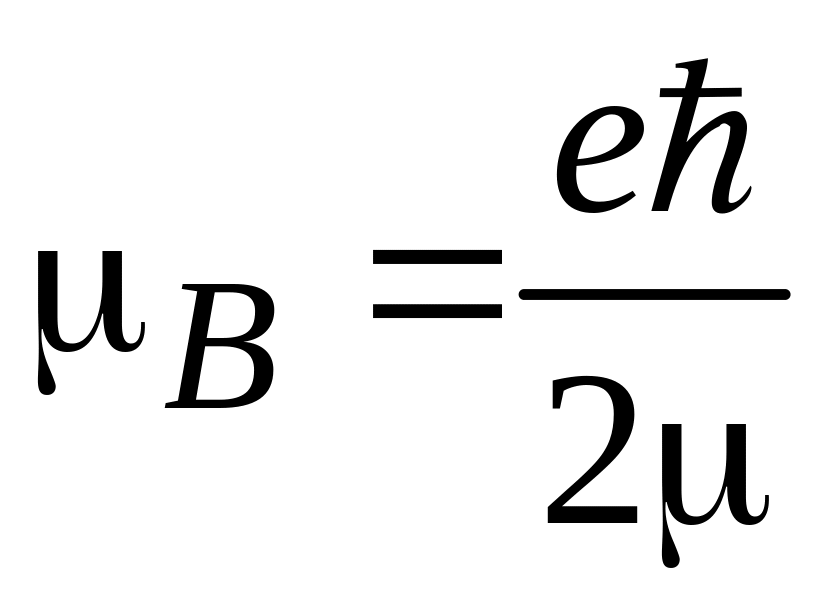 – магнетон Бора.
Для состояния
– магнетон Бора.
Для состояния
![]() с определенной проекцией орбитального
момента стационарное уравнение Шредингера
с определенной проекцией орбитального
момента стационарное уравнение Шредингера
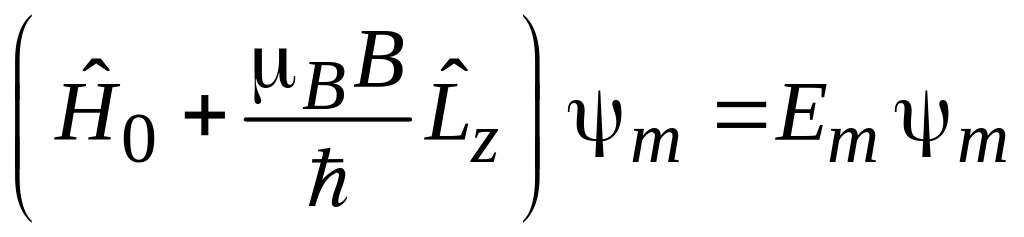 .
.
Учитывая
![]() ,
находим энергию состояния
,
находим энергию состояния
![]() ,
(П.7.16)
,
(П.7.16)
где Е0 – энергия без учета магнитного поля.
Результат
получается и в квазиклассическом
приближении. Магнитный момент орбитального
движения электрона (1.37)
![]() ,
помещенный в магнитное поле
,
помещенный в магнитное поле
![]() ,
получает дополнительную энергию
,
получает дополнительную энергию
![]() .
.
