Примеры

1. Найти состояния свободного плоского ротатора.

Если тело вращается вокруг оси z, проходящей через центр масс и совпадающей с одной из трех осей инерции, то момент центробежных сил инерции равен нулю, ось вращения неподвижная и тело называется плоским ротатором. При отсутствии потенциального поля, радиального движения и движения по оси z, из (5.15) находим гамильтониан . Уравнение Шредингера получает вид

.

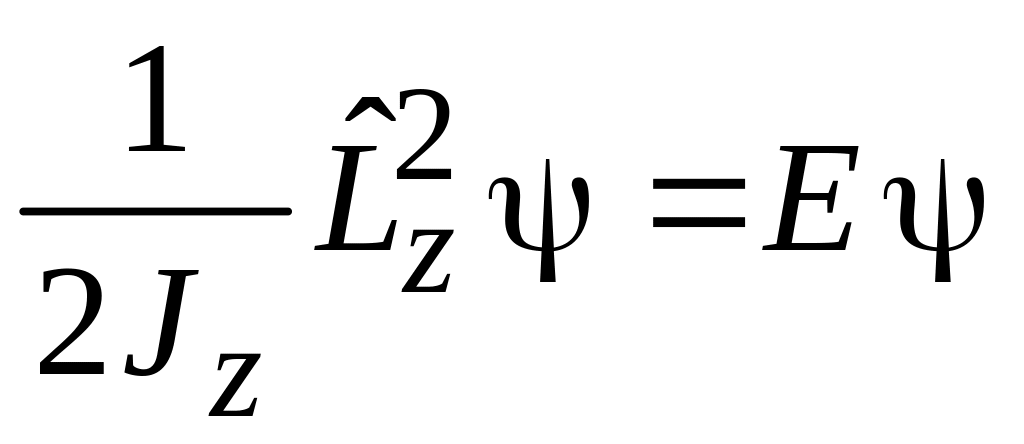Следовательно, – собственная функция оператора ,

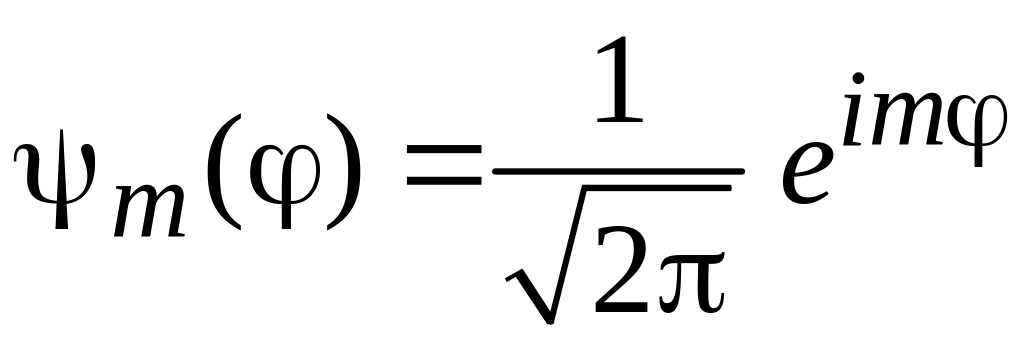, (П.6.1)

Уровни энергии

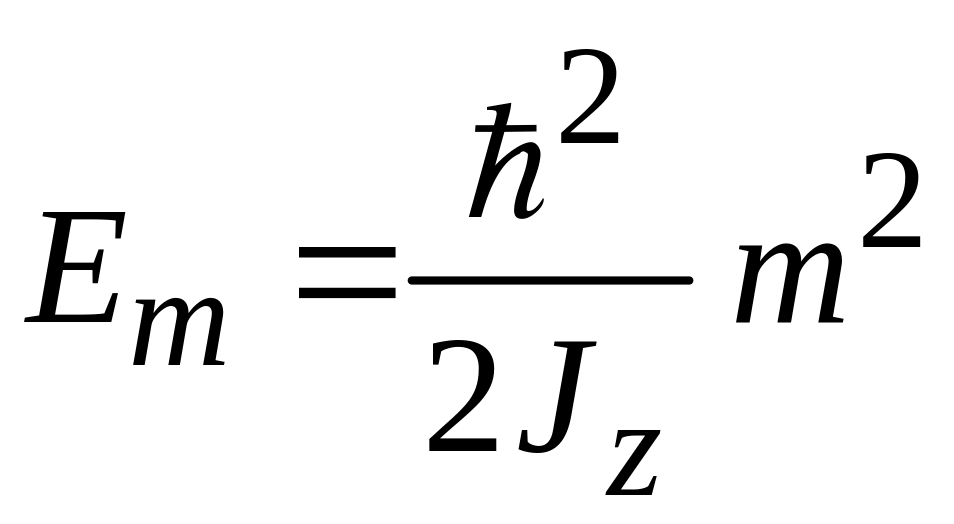(П.6.2)

при вырождены двукратно, т. к. .

6.5. Найти состояния частицы в цилиндрической полости, свободной от полей. Стенка полости радиусом а и длиной образующей s абсолютно непроницаемая.

При выполняется и уравнение (5.18)

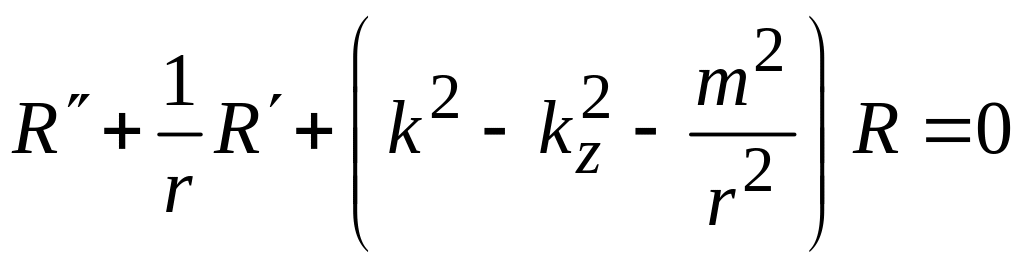
является уравнением Ломмеля, решение

,

,

где

, ,

Краевые условия дают , , где Краевое условие дает , где – корень функции Бесселя ; i – порядковый номер корня. В частности:

; ; ; ; ; .

В результате

, .

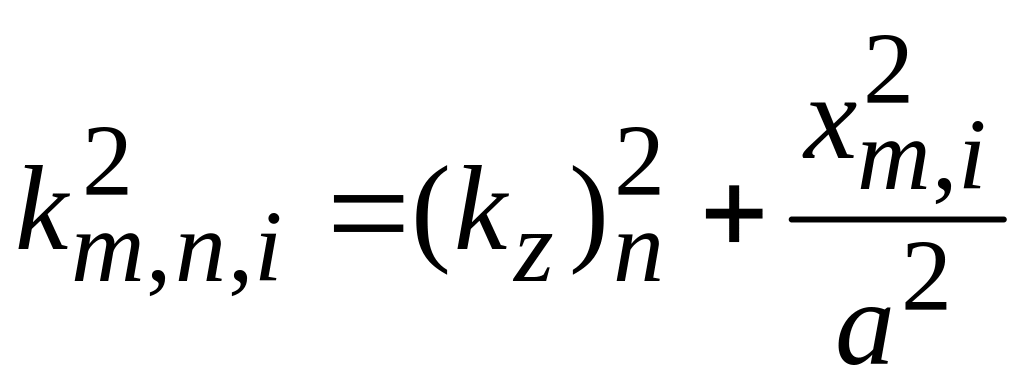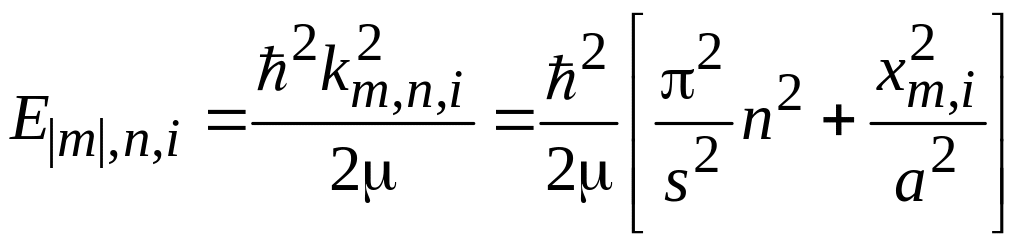Водородоподобный атом

В электронной оболочке водородоподобного атома находится один электрон, например , заряд ядра . Электрон имеет потенциальную энергию .

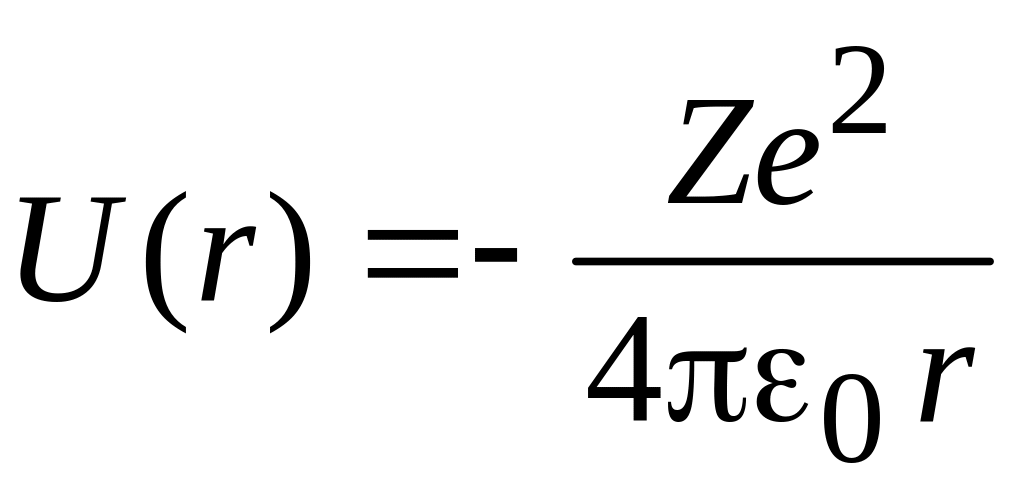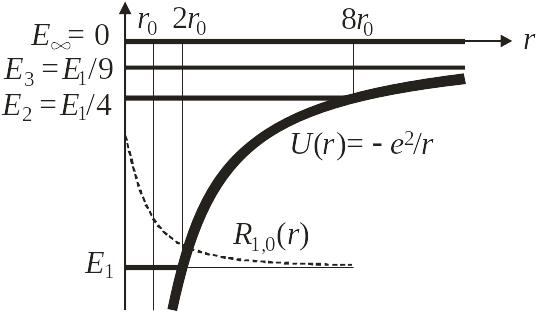
Рис. 5.1. Уровни атома водорода

Уравнение состояния. Учитывая центральную симметрию системы, для связанного состояния используем волновую функцию (5.9)

.

Из (5.10) получаем

.

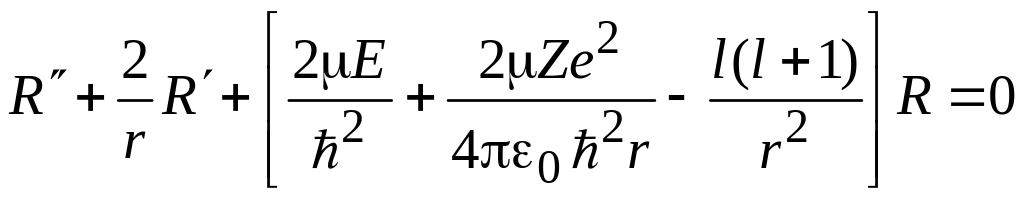Энергию выражаем через безразмерный параметр

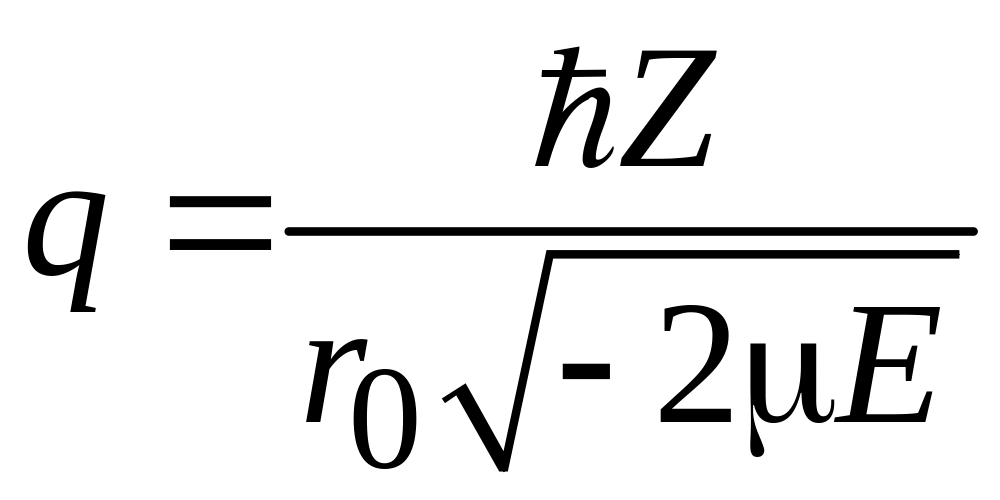, (5.21)

где

(5.22)

– боровский радиус атома водорода. Используем безразмерную переменную

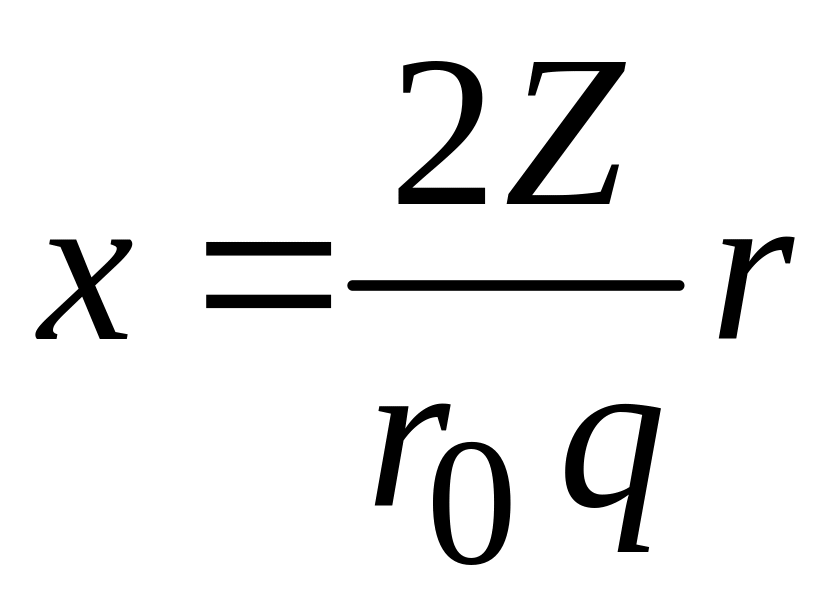, . (5.23)

Для получаем уравнение обобщенного гипергеометрического типа

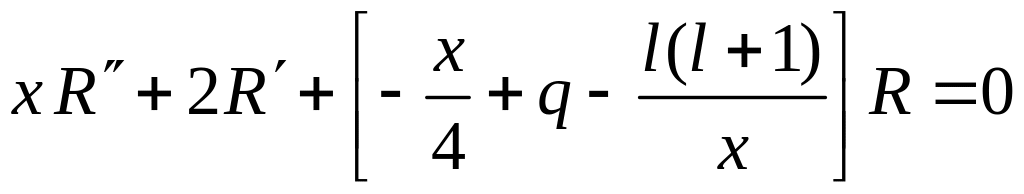. (5.24)

Существование нормы решения дает – радиальное квантовое число. Решение выражается через обобщенный полином Лагерра

, (5.25)

где . При N не целом решение выражается бесконечным рядом и при ведет себя как , поэтому норма волновой функции не существует.

Квантовые числа. Пространственная и угловая ограниченность движения приводят к дискретности спектра квантовых чисел, характеризующих состояние электрона. Эти числа соответствуют сохраняющимся величинам – энергии, моменту импульса и проекции момента импульса.

Радиальное квантовое число определяет степень полинома, входящего сомножителем в радиальную функцию, и число ее нулей.

Главное квантовое число

определяет энергию электрона. Множество состояний с одинаковым называется слоем и обозначается, соответственно: K, L, M, N,…

Орбитальное квантовое число l определяет модуль момента импульса электрона. С учетом , находим

.

Множество состояний с одинаковым называется оболочкой и обозначается, соответственно: s, p, d, f,…

Магнитное квантовое число определяет проекцию момента импульса электрона. Число состояний с одинаковым l равно .

Основное состояние: , , .

Полная энергия следует из (5.21)

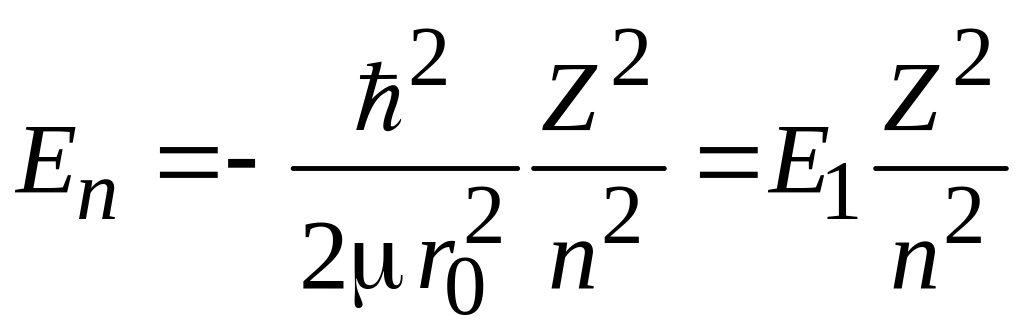, (5.26)

где

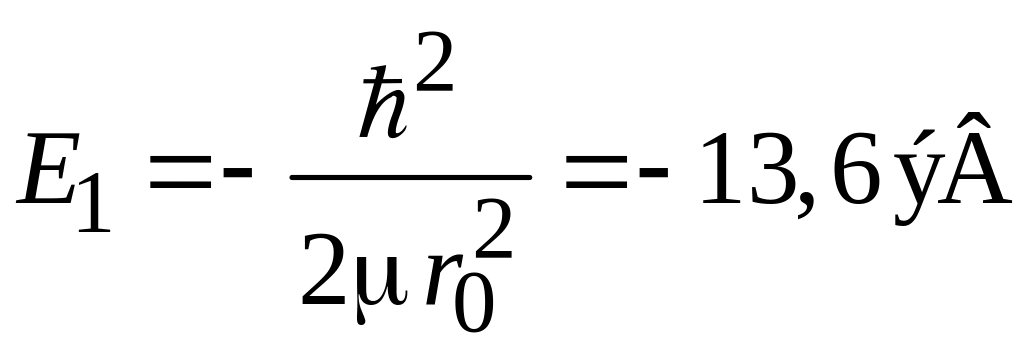
– энергия основного состояния атома водорода. Энергия не зависит от l и m. Кратность вырождения состояния n равна числу состояний с одинаковым n, тогда без учета спина электрона получаем

.

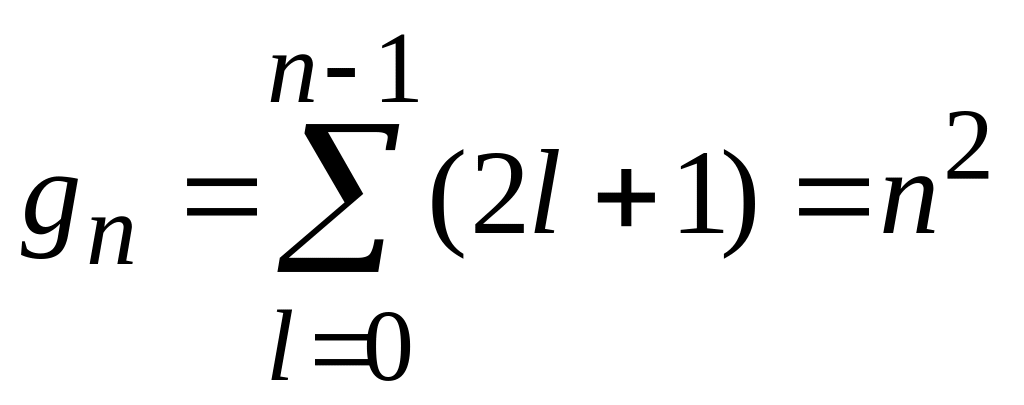Радиальная функция. Учитывая , и полагая 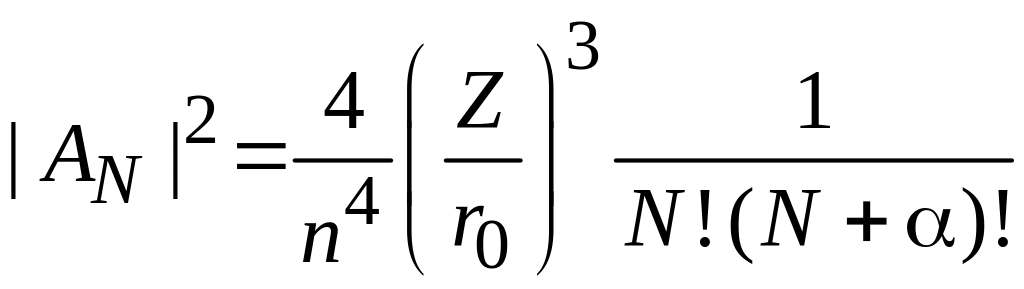, из (5.25) получаем

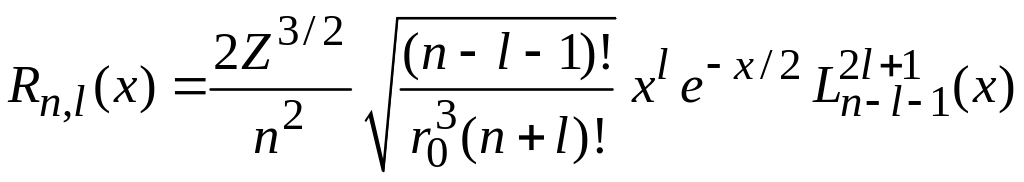. (5.27)

Выполняется условие нормировки

, . (5.28)

Для атома водорода находим

, , ;

,

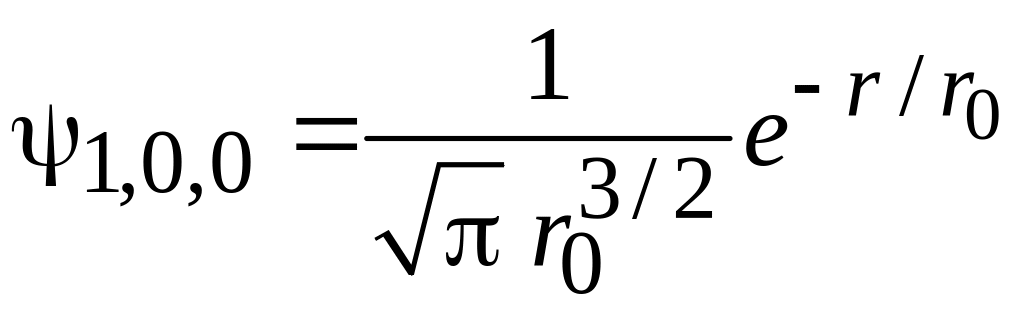– основное состояние,

, ,

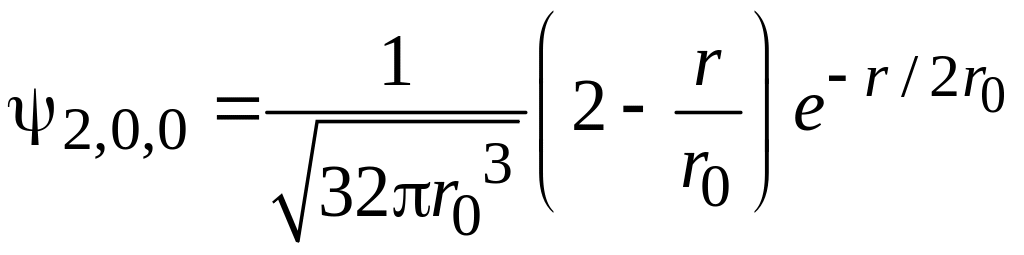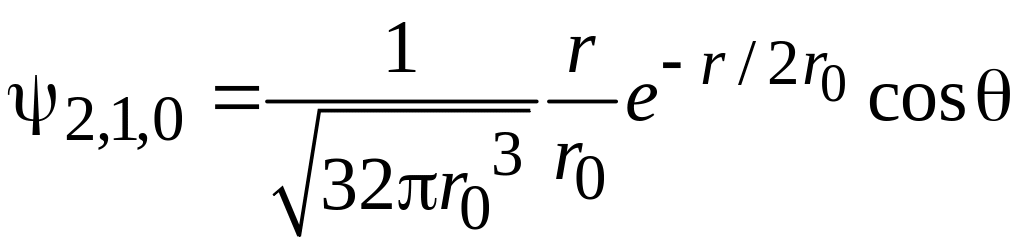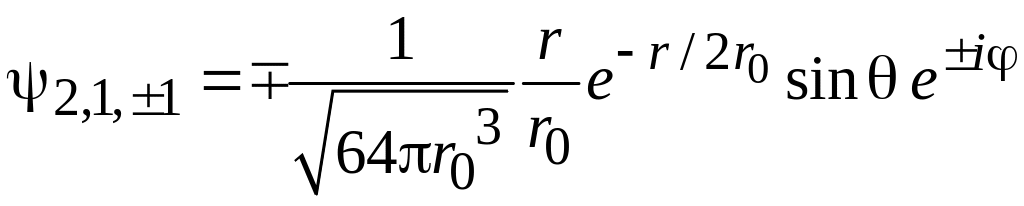. (5.30)

Состояния нормированы

. (5.31)

Ридберговский атом имеет высоковозбужденное состояние электрона с квантовыми числами . Для возбуждения атома используется лазер с перестраиваемой частотой. Далее состояние преобразуется в волновой пакет кратковременным облучением атома микроволновым излучением, что приводит к локализации электрона. К такому состоянию применима квазиклассическая теория атома Бора. Размер ридберговского атома достигает макроскопических величин. Получены возбужденные состояния атома калия с диаметром траектории электрона ~1 мм, что соответствует . Частоты переходов между соседними состояниями с большими квантовыми числами находятся в микроволновой области, а не в оптической, как для низко возбужденных состояний. Электрический дипольный момент атома P_E пропорционален его размеру, поэтому велика энергия взаимодействия атома с внешним электрическим полем .