Центральносимметричные и осесимметричные стационарные системы

Гамильтониан стационарной системы

. (5.1)

Центральная симметрия означает отсутствие в сферических координатах угловой зависимости

.

Осевая симметрия означает отсутствие в цилиндрических координатах угловой зависимости

.

Особенностью центрально- и осесимметричных систем является сохранение момента импульса.

Уравнение Шредингера в сферических координатах

Гамильтониан центрально-симметричной системы складывается из кинетических энергий радиального и углового движений и из потенциальной энергии. С учетом (5.1), (4.8) и (4.9) получаем

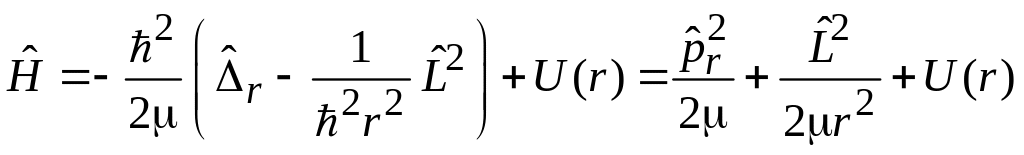. (5.7)

Из (4.5) и (5.7) находим

, , .

Момент импульса и одна из его проекций сохраняются с течением времени и имеют определенные значения вместе с энергией. Состояние характеризуется собственными значениями операторов , т. е. числами Е, l, m.

Радиальный импульс. Из (4.9)

. (5.8)

Уравнение Шредингера получает вид

.

Решение ищем в виде

.

Подстановка в уравнение, умноженное на 2μr² и деленное слева на ψ, дает

.

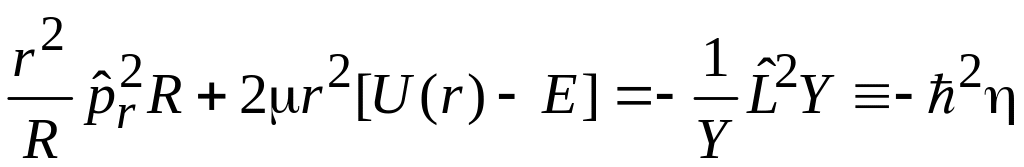Уравнение для аналогично уравнению (4.14) , поэтому и – сферическая функция. Уравнение для R дает

,

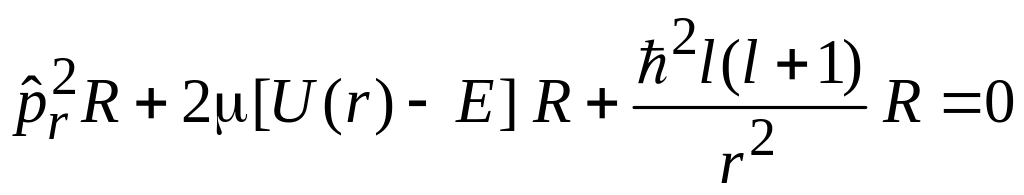тогда

. (5.9)

Радиальное уравнение с учетом (5.8) получает вид

. (5.10)

Замена (5.4)

(5.11)

с учетом дает уравнение, аналогичное (3.1):

, (5.12)

где ; ;

(5.13)

– эффективная потенциальная энергия включает центробежную энергию отталкивания от оси вращения.

Конечность требует

. (5.14)

Условие ортонормированности (5.6) для дискретного спектра

, .

Для уравнения (5.12) и решения применимы краевые условия из раздела 3.2.

Уравнение Шредингера в цилиндрических координатах

Гамильтониан системы с осью симметрии Oz

, (5.15)

где:

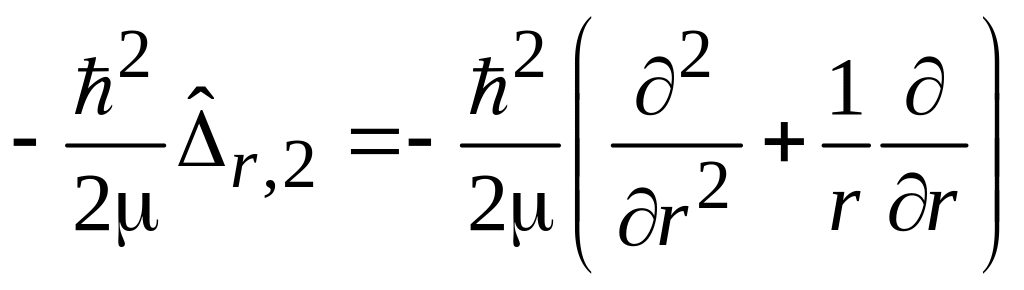– энергия радиального движения в плоскости (x,y);

– энергия вращения в плоскости (x,y), , – момент инерции;

– энергия движения по оси z, – оператор проекции импульса.

Если не зависит от z, то

, , .

Проекция момента импульса на ось z и импульс вдоль этой оси сохраняются с течением времени и имеют определенные значения вместе с энергией. Состояние характеризуется собственными значениями операторов , или числами , и m:

.

Стационарное уравнение Шредингера получает вид

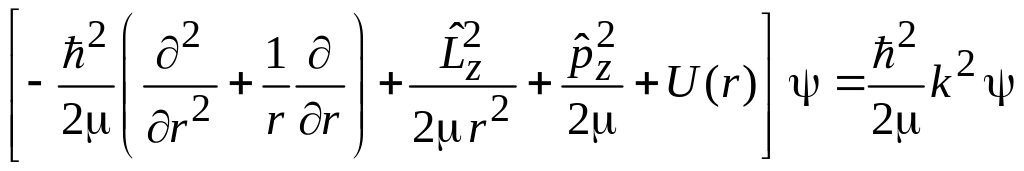. (5.16)

Переменные r, z и  разделяются. С учетом

,

ищем решение в виде

. (5.17)

Подставляем (5.17) в (5.16) и получаем радиальное уравнение

, (5.18)

где , поскольку уравнение содержит m².

Замена (5.4)

с учетом 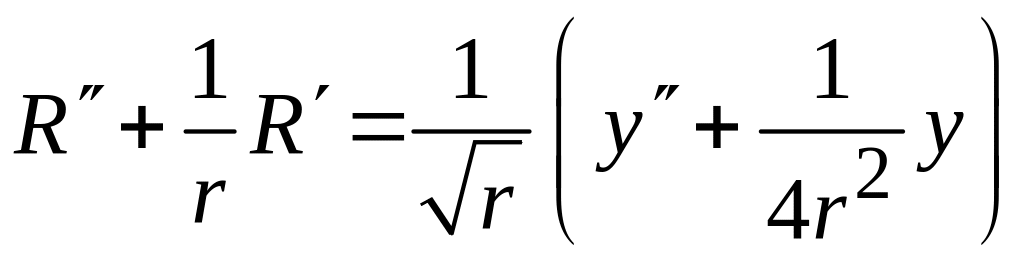устраняет первую производную и дает уравнение

(5.19)

с условие (5.14) . Эффективная потенциальная энергия

.

Ортонормированность функций дискретного спектра имеет вид (5.6)

. (5.20)

Для уравнения (5.19) и решения применимы краевые условия из раздела 3.2.