Локализация Андерсона

Примесный атом. В периодическом поле кристалла электрон с энергией, совпадающей с уровнем в разрешенной зоне, описывается волной Блоха и рассматривается как свободная квазичастица, обнаруживаемая в любом месте кристалла. При нарушении периодичности, вызванной примесным атомом, происходит захват электрона атомом. Состояние электрона оказывается в запрещенной зоне. Явление описал Ф. Андерсон в 1958 г.

Спектральное уравнение. Атом примеси в точке x₀ кристалла создает возмущение потенциальной энергии электрона . Для получения состояний электрона используем уравнение Шредингера

,

где – гамильтониан в невозмущенной решетке конечного размера. Решение разлагаем по базису N невозмущенных функций спектра разрешенной зоны

. (3.89)

Для нахождения энергии E и коэффициентов подставляем разложение в уравнение, учитываем и получаем

.

Для извлечения из суммы коэффициента c_m умножаем уравнение на , интегрируем по объему кристалла и используем

, ,

тогда получаем

. (3.90)

Учитывая (3.89), находим

. (3.91)

Подстановка и в (3.90) дает

.

Приводим к общему знаменателю и получаем алгебраическое уравнение

. (3.92)

Анализ уравнения. Уравнение степени N имеет N корней для энергий N возмущенных уровней. В левой стороне находится полином степени N, в правой – степени (N – 1).

При слабом возмущении правая сторона (3.92) равна нулю. В левой стороне энергия принимает одно из невозмущенных значений – спектр не изменяется.

При сильном возмущении в виде отталкивания , или притяжения энергия растет. В левой стороне (3.92) главный вклад дает наибольшая степень Е, тогда для одного из решений получаем . Остальные решений конечные и для них из (3.92) следует уравнение степени

,

корни которого близки корням невозмущенного уравнения. Следовательно, при локальном возмущении кристаллической решетки один уровень разрешенной зоны отщепляется и при поднимается вверх, при опускается вниз. В запрещенной зоне появляется состояние _л. Остальные уровни практически не меняют своего положения.

Состояние в запрещенной зоне разлагаем в ряд (3.89) с коэффициентами (3.91)

,

где учтено и при . Тогда получаем

,

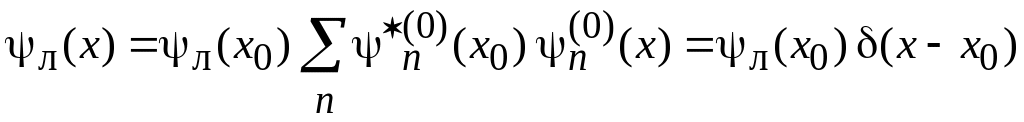где использована полнота базиса . Следовательно, при сильном возмущении электрон в запрещенной зоне локализован в области возмущения . Чем слабее возмущение, тем ближе энергия электрона к разрешенной зоне и больше область локализации. При локализованное состояние переходит в нелокализованное состояние разрешенной зоны, обнаруживаемое в любом месте кристалла.

Уровни Тамма

Кристалл со свободной границей в виде барьера при имеет

,

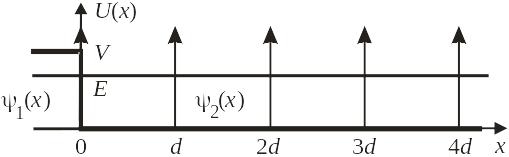
где Н(x) – функция Хевисайда; V – потенциальный барьер на поверхности кристалла. Уравнение Шредингера (3.1) имеет вид

. (3.93)

При , получаем

, . (3.94)

Используем убывающее решение

.

При уравнение (3.93) совпадает с (3.75) и получаем решение (3.76)

.

В общем случае квазиимпульс комплексный

,

Q₁ и Q₂ – вещественные.

Для вещественного квазиимпульса решение совпадает с волной Блоха в неограниченной решетке, энергия имеет зонную структуру.

Для комплексного квазиимпульса решение и энергия зависят от Q₂. У кристалла со свободной поверхностью появляются состояния в запрещенной зоне, называемые уровнями Тамма, локализованные в поверхностном слое толщиной . Возможность существования состояний электрона вблизи поверхности кристалла обосновал И.Е. Тамм в 1932 г.

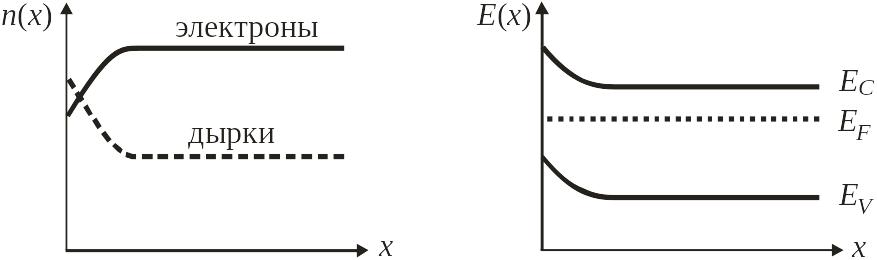
Объемная концентрация собственных носителей тока в полупроводнике , поверхностная концентрация . Плотность поверхностных уровней в слое толщиной . Поверхностные уровни изменяют концентрацию свободных электронов и дырок в поверхностном слое, изгибают границы энергетических зон. На рисунке показан полупроводник n-типа с поверхностными состояниями акцепторного типа, обогащающими поверхностный слой неосновными носителями – дырками. В результате изменяется работа выхода, размывается энергетический спектр, происходит рассеяние носителей тока, уменьшается длина свободного пробега и длина когерентности волны де Бройля. В микроэлектронике используются гетероструктуры с близкими кристаллографическими характеристиками, где одна кристаллическая решетка переходит в другую без образования открытой поверхности.

116