Примеры

1. Найти коэффициент прохождения электрона с энергией Е из металла в вакуум под действием внешнего электрического поля напряженностью E.

При образовании кристаллической решетки простого металла валентные электроны отрываются от атомов, становятся свободными и при низкой температуре имеют полную энергию , где – энергия Ферми. При низкой температуре длина свободного пробега электрона ~ межатомных расстояний (~1 см). На границе металл–вакуум на электрон действуют возвращающие силы со стороны нескомпенсированных положительных ионов решетки и электронного облака, окружающего металл. Объем металла для электрона является потенциальной ямой с работой выхода . Тепловая энергия активизирует электроны вблизи уровня Ферми и основная масса электронов не может покинуть металл. Если электрическое поле E направить к металлу, то график потенциальной энергии наклоняется. Ширина потенциального барьера становится конечной и происходит туннельный эффект, называемый холодная или автоэлектронная эмиссия электронов. Явление обнаружил Роберт Вуд в 1897 г., исследовали Ральф Фаулер и Лотар Нордгейм в 1928 г.

Однородное поле E создает при распределение потенциала и потенциальной энергии электрона

, .

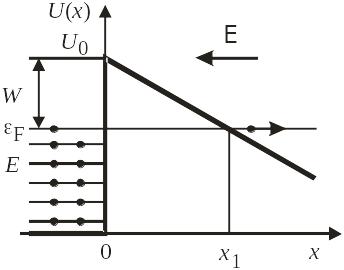
Протяженность барьера на уровне Ферми находим из , ,

.

Из (3.73)

получаем

,

.

Заменяем , находим , тогда

, (П.4.1)

где эффективное задерживающее поле

.

Автоэлектронная эмиссия дает плотность тока до 10¹⁰ А/см², используется в электронных микроскопах, рентгеновских трубках, приемниках инфракрасного излучения.

2. Найти коэффициенты отражения и прохождения через барьер частицы с .

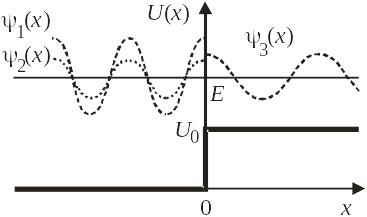
Из (3.2)

,

при и получаем падающую, отраженную и проходящую волны

, , .

, ,

Граничные условия (3.11) и (3.12) при дают

, ,

откуда

, , (П.4.2)

,

.

При происходит полное отражение .

Замена преобразует рисунок к виду

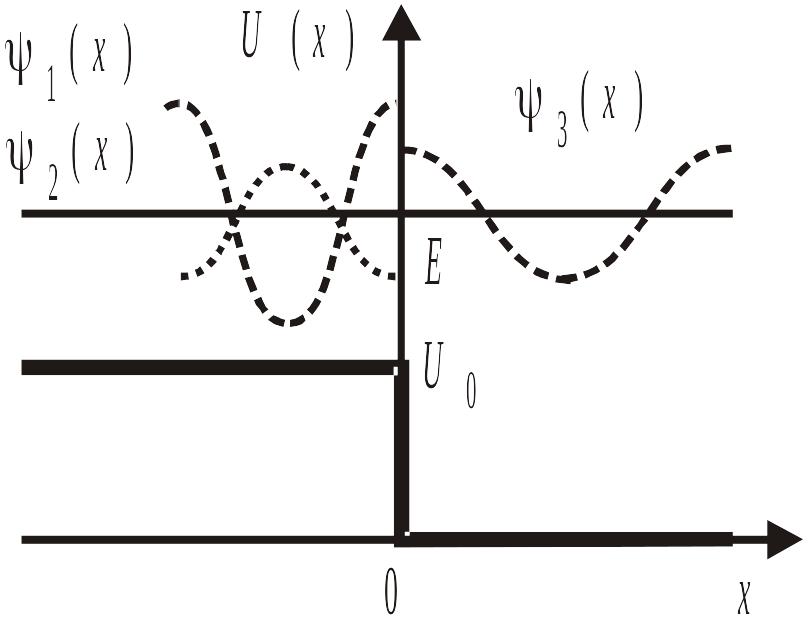
при этом

, . (П.4.3)

Функции R(E) и T(E) не изменяются – обращение движения частицы через барьер не изменяет коэффициентов отражения и прохождения.

3. Амплитуду прохождения t через систему локальных барьеров 1 и 2, показанную на рис. 3.17, выразить через амплитуды прохождения , и отражения , каждого из барьеров по отдельности. Между барьерами расстояние a, волновое число частицы k. При распространении волн сохраняется фазовая когерентность.

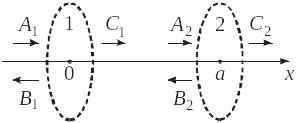
Рис. 3.17. Система барьеров

Для одиночных барьеров используем соотношения между падающими , отраженными и проходящими волнами

, , , .

Для системы барьеров

.

Учитывая отражение волны от барьера 1 с амплитудой , а также изменение фаз волн на пути между барьерами, находим

,

откуда

,

,

тогда

. (П.4.4)