Одномерное рассеяние
Частица с энергией
Е
движется вдоль
оси x
и попадает в поле
.
Падающая волна рассеивается, возникает
отраженная и проходящая волны.
Из уравнение
Шредингера (3.2) при
получаем
,
.
Частные решения:
при
падающая
волна
(3.62)
и отраженная волна
;
(3.63)
при
проходящая
волна
.
(3.64)
Амплитуды r и t – комплексные.
Из (2.72)
находим проекции плотности тока
вероятности падающей, отраженной и
проходящей волн
,
,
.
(3.65)
Коэффициент отражения (reflection)
,
(3.66)
тогда
.
(3.67)
Коэффициент прохождения (transmission)
,
(3.68)
тогда
.
(3.69)
Условие унитарности. Из уравнения непрерывности тока вероятности (2.73) следует
.
(3.70)
Подставляем (3.67) и (3.69) в (3.70) и получаем условие унитарности, от лат. unitas – «одно целое»:
(3.72)
– сумма вероятностей всех возможных процессов в системе, т. е. отражения и прохождения, равна единице.
Туннельный эффект
Прохождение барьера, недоступного для классической частицы, называется туннельным эффектом. Георгий Антонович Гамов в 1928 г. объяснил парадокс, связанный с α-распадом
.
Два протона и два нейтрона ядра урана объединяются и образуют α-частицу с энергией 4,18 МэВ. Задерживающий потенциал ядра урана составляет 8,57 МэВ. Тем не менее, ядро может распасться благодаря туннельному эффекту.
Частица с полной энергией Е в виде волны
распространяется
вдоль оси x
и встречает барьер
при
.
Возникает отраженная волна
.
Внутри барьера, согласно квазиклассическому приближению (3.60), волна экспоненциально затухает
.
За барьером
.
Коэффициент
прохождения барьера.
Из (3.68) при
находим
.
Соотношение
следует из условия сшивания (3.11) при
условии малости отраженной волны.
Учитывая
,
,
,
в квазиклассическом приближении с точностью до слабо меняющегося и близкого к единице предэкспоненциального множителя находим
.
(3.73)
Для прямоугольного
барьера шириной
и высотой
из (3.73) получаем
.
Проницаемость
барьера существенна при
,
тогда
,
.
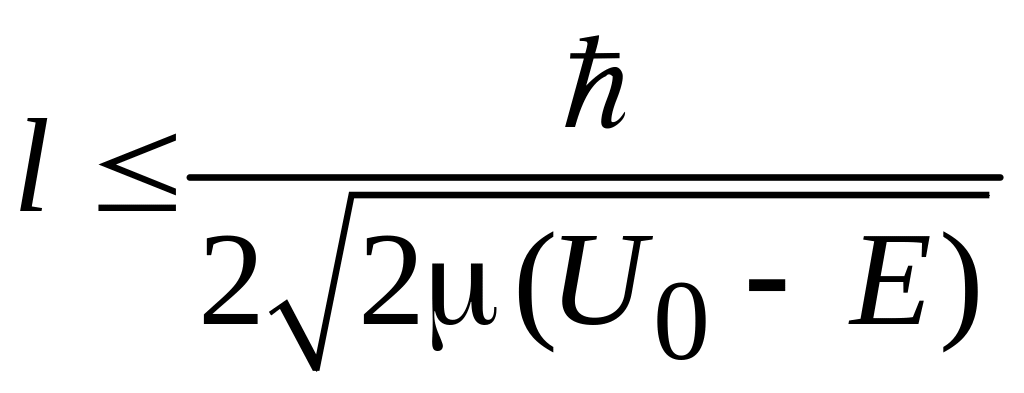(3.74)
Чем меньше масса частицы, тем более широкий и высокий барьер она преодолевает. Для макроскопического тела туннельный эффект не проявляется.
Объяснение
туннельного эффекта
основано на соотношении неопределенностей
(2.37)
.
Если частица обнаруживается внутри
барьера шириной l,
то
,
тогда
.
Это дает дополнительную кинетическую
энергию
.
Суммарная энергия
обеспечивает преодоление барьера шириной (3.74).