Одномерные стационарные задачи

Уравнение Шредингера для двухмерных и трехмерных стационарных систем с потенциальной энергией сводится в ряде случаев к одномерному уравнению Шредингера (2.59)

, (3.1)

или

, . (3.2)

Общее решение содержит полную энергию Е и два свободных параметра. Эти величины находятся из граничных условий и из нормировки волновой функции.

Одномерные стационарные состояния

Переход к одномерной задаче. Трехмерная стационарная система описывается в декартовых координатах уравнением Шредингера (2.57)

.

Если

,

то волновая функция факторизуется

и уравнение распадается на независимые одномерные уравнения

, ,

где

; .

Свободная частица. При уравнение (3.2) имеет общее решение

, . (3.3)

Волны распространяются по- и против оси x. Если краевые условия не накладываются, то спектр непрерывный .

Плотность тока вероятности находим из (2.72)

, ,

, . (3.6)

Задавая плотность электрического тока, получаем , и из (3.6) находим амплитуды волн .

Частица в потенциальном ящике. Внутри ящика размером L, где , частица с энергией Е описывается функцией (3.3). Учтем стенки ящика. Для этого расширяем определение функции на все пространство, рассматривая систему повторяющихся ящиков, и вводим периодическое условие Борна–Кармана:

. (3.8)

Подстановка (3.3) в (3.8) дает . Учитывая , где , находим, что волновое число, импульс и энергия частицы в ящике квантуются

, , ,

.

Для кристалла с характерным размером получаем расстояние между уровнями . Сравниваем с тепловой энергией частицы газа при нормальной температуре . При достаточно высокой температуре и большом ящике спектр энергии квазинепрерывный.

Состояние n занимает в координатном пространстве объем , в импульсном пространстве – , в фазовом пространстве

. (3.9)

Любое состояние в потенциальном ящике занимает фазовый объем, равный постоянной Планка.

Граничные условия для прямоугольных потенциалов

Квантовые эффекты существенны, если потенциальная энергия существенно изменяется на расстояниях порядка длины волны де Бройля. Этому условию удовлетворяют прямоугольные потенциалы, возникающие на границах металла, полупроводника, на примесях и дислокациях, в полупроводниковых гетероструктурах. Для частицы в такой системе найдем энергию и волновую функцию.

Алгоритм решения стационарного уравнения Шредингера:

1. Область определения волновой функции разбивается на участки непрерывности потенциальной энергии, на границах она изменяется скачком. На всех участках полная энергия частицы одинакова.

2. Для каждого участка записывается уравнение Шредингера и находится общее решение для волновой функции со свободными параметрами.

3. Функции соседних интервалов «сшиваются» в точках скачка потенциала. Это дает параметры и уравнение для возможных значений энергии.

4. Условие нормировки волновой функции, учитывающее все интервалы, дает последний параметр задачи.

Условия «сшивания» получим путем однократного и двукратного интегрирования уравнения Шредингера по бесконечно малому интервалу координат около точки скачка потенциала.

Конечный скачок потенциала при . Выполняем двукратное интегрирование уравнения (3.1)

по интервалу , . Для конечной функции используем

, ,

тогда

.

В результате

,

. (3.11)

Волновая функция и плотность вероятности непрерывны в точке конечного скачка потенциала.

Однократное интегрирование (3.1) дает . Первая производная волновой функции и плотность тока вероятности непрерывны в точке конечного скачка потенциала

,

. (3.12)

-образный потенциал

,

где V – среднее по единичному интервалу значение потенциальной энергии. Однократное интегрирование (3.1) с учетом дает

. (3.13)

Первая производная волновой функции в точке -образного потенциала имеет разрыв, пропорциональный величине функции. При и возможный график показан на рисунке.

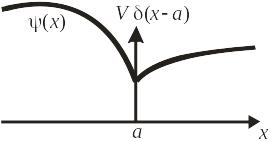
При двукратном интегрировании (3.1) учитываем

,

где Н – функция Хевисайда. Волновая функция и плотность тока вероятности непрерывны в точке -образного скачка потенциала.

Бесконечный потенциал на конечном интервале. Уравнение (3.1) существует, если во всех точках интервала

. (3.14)