5. Моделирование оптимального управления поездами метрополитена

Представленное здесь моделирование оптимального управления поездами метрополитена выполнено профессором Ходаковским В. А. [39,40,41,42].

Постановка задачи: На некоторой линии метро используется n – позиций положения поездов (станций, тупиков, мест на перегонах, оборотных тупиков, съездов), которые задаются условной точкой А_i { i = 1,2,…n}.

Расстояния между указанными позициями, отсчитываемые по рельсам с учетом направления движения поездов и возможных оборотов, известны. Поезда движутся, перемещаясь из одной позиции в другую, по графику в одном направлении в заданной последовательности, которая определяется местами их ночных стоянок в заданных позициях, плановым графиком ремонта и другими факторами.

Вследствие различных причин, график движения поездов нарушается, в результате чего поезда начинаю следовать не в той последовательности, которая требуется по плану – графику. При управлении движением каждому поезду выдаются команды на перемещение в соответствующие позиции. Существуют общие и частные команды. По общей команде все поезда перемещаются на одну позицию по направлению движения. Частные команды даются конкретным поездам.

Задача состоит в поиске такой последовательности общих и частных команд управления поездами, в результате применения которой поезда расположатся в нужной последовательности (очередности) друг за другом за минимальное время, либо с минимальным потреблением электроэнергии.

Математическая постановка задачи: Линия метрополитена может быть представлена как некоторый граф с узлами, соответствующими возможным позициям положения поездов, и ребрами, соответствующими расстояниям между этими позициями (либо интервалам времени, необходимым для преодоления поездом этих расстояний при заданной скорости). Вершинам графа поставлена в соответствие матрица D размерностью [n, n], в которой размещены числа n_шаг(i , j), соответствующие числу минимальных шагов управления, необходимых для перемещения поезда из узла i в узел j при применении оптимальной стратегии по выбранному критерию. При этом под шагом управления понимается выдача общей, или частной команды управления. Оптимальная стратегия определяется топологией линии (связями в графе). Таким образом, матрица D может быть записана в виде

. (1)

С матрицей D связана матрица OpU(i ,j), элементами которой являются оптимальные векторы управления для перемещения некоторого поезда из узла i в узел j, причем размерность этих векторов равна числу n_шаг(i , j). В указанных векторах хранятся числа, соответствующие кодам (номерам) частных матриц управления U_i.

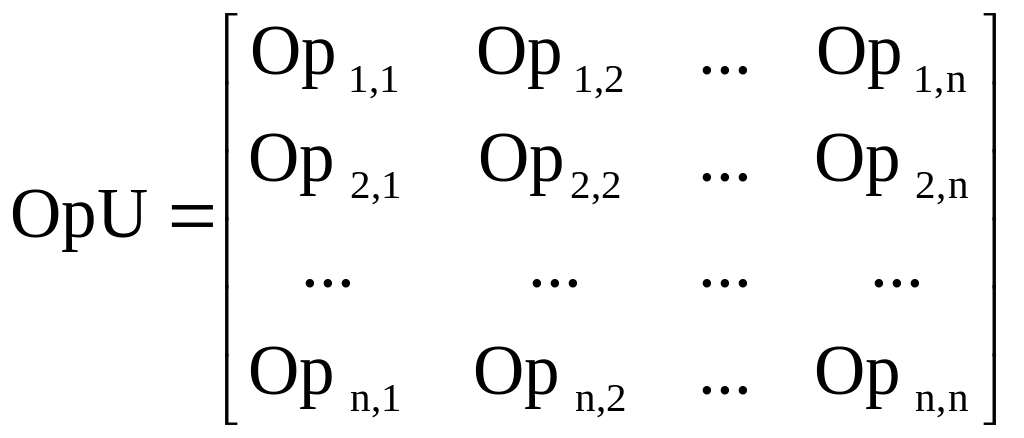(2)

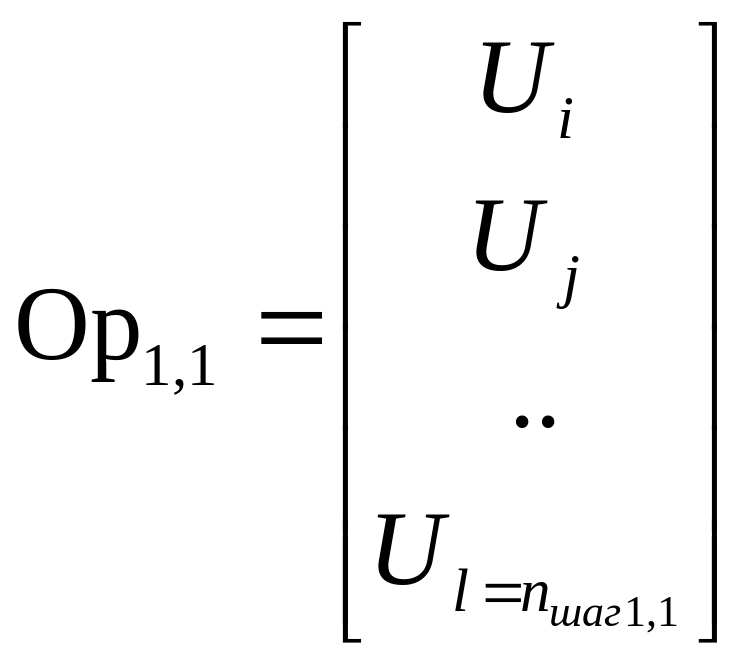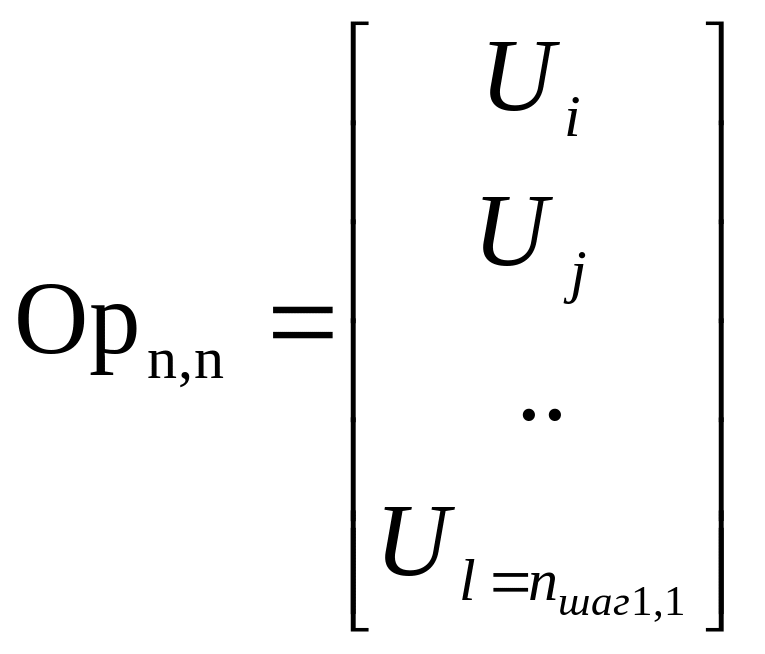…. (3)

При управлении движением поездов возможны различные управляющие воздействия

(U_i), i = 1, 2,.., m. (4)

Число управляющих воздействий m определяется связями графа. Каждое из этих управляющих воздействий представляет собой частную матрицу управления размерностью [n , n]. Все элементы частной матрицы управления равны нулю, за исключением элементов в тех строках и столбцах, на которых стоят единицы, и которые указывают на начальный узел перемещения (столбец) и на конечный узел перемещения (строка) конкретного поезда.

Для решения задачи задаются два вектора: вектор Tek[ n] текущего положения поездов на узлах, и вектор Treb[n] требуемого положения поездов на узлах. Указанным векторам соответствует матрица Str[2,n] стратегии управления, размерность которой по столбцам равна числу несоответствий в содержании векторов Tek[ n] и Treb[n] (то есть числу циклов перемещений всех поездов, которые стоят не в требуемых позициях), а размерность по строкам равна 2, причем в первой строке хранятся номер узла из которого необходимо убрать поезд, а во второй – соответственно номер узла, в который необходимо поставить поезд.

(5)

Решение поставленной выше задачи состоит в поиске такого управления поездами (выборе последовательности управляющих воздействий или произведений частных матриц управления),

), (6)

применение которого расположит поезда в нужной последовательности (очередности) друг за другом при минимальном числе шагов управления, то есть при котором

UTek = Treb. (7)

Фактически требуется найти последовательность минимальных путей в данном графе на каждом шаге управления, которые позволяют при использовании всех не занятых узлов оборота, пройти по ребрам за минимальное время. При этом поезд, занимающий неправильную позицию, и место, которое он должен в итоге занимать, приближаются друг к другу, двигаясь по минимальному пути в графе на каждом шаге управления.

Общая постановка такой задачи соответствует задаче динамического программирования с выбором оптимального управления на каждом шаге управления k.

Целевая функция управления представляет собой сумму всех шагов, которые необходимо совершить, начиная с текущего k – того шага управления, чтобы получить требуемое положение поездов на линии

, (8)

На каждом шаге выбирается такая частная матрица управления U_i , являющаяся первым элементом во всех векторах Op_i,j, требуемых для исполнения в соответствии с текущим содержанием матрицы Str, применение которой дает наибольшую разницу

 = f(k +1) – f(k) то есть   max. (9)

Решение задачи. Для проверки указанной методики решения задачи выбран пример с количеством узлов n = 30. Граф данного примера приведен на Рис.5.6.1. В примере используется два узла перегона (26, 28) с оборотными тупиками (25, 27), два концевых тупика (24, 29), семь станций: 1 – я с1 =(1, 23), 2 – я с2 =(2, 22), 3 – я с3 =(4, 20), 4 – я с4 =(6, 18), 5 – я с5 =(7, 17), 6 – я с6 =(9, 15), 7 – я с7 =(11, 13), а остальные узлы обозначают положения поездов на перегонах.

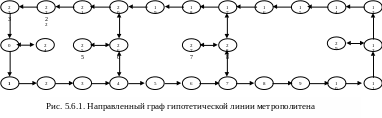
Из 3 – х строк и 11 столбцов, которая связана с графом Рис.1., причем

Для моделирования и поиска решения выбрана среда MATHCAD – 2000. При этом текущий и требуемый векторы положения поездов задавались как векторы столбцы с размерностью 1х30, но для удобства анализа эти векторы отображаются в виде матрицы из 3 – х строк и 11 столбцов, которая связана с графом Рис.5.6.1., причем числа, стоящие в матрице и не равные “0” или “88” соответствуют номеру поезда, “ ” – пустая позиция, в которой поезда нет, а “88” – позиция, в которую поезд не попадает. Ниже приведены указанные матрицы.

	С1	с2		с3		с4		с5		с6	с7
пр		9		11		10		1		8	
	6				88			88	88		7
об		2		3		4		5		12	

Текущее положение:

		с1				с2				с3				с4			с5				с6		с7
п Требуемое положение: р						12				11				10			9				8		
		1										88					88		88				7
об						2				3				4			5				6		

	с1	с2		с3		с4		с5		с6	с7
пр	23	22	21	20	19	18	17	16	15	14	13
	0	24	25	26	88	27	28	88	88	29	12
об	1	2	3	4	5	6	7	8	9	10	11

Таблица узлов:

(позиций)

Анализ текущей и требуемой позиций позволяет сделать вывод, что не в своих позициях стоят четыре поезда № 1, № 6, № 9, № 12.

Для данной топологии существует 17 частных матриц управления. Первая из них является общей и позволяет переместить все поезда, стоящие на станциях или перегонах, в следующую позицию по ходу движения, указанному в таблицах положений стрелкой. Первый поезд находится в позиции №16 на станции с5, а должен находиться в позиции “0” на станции с1. для перемещения этого поезда можно применить несколько стратегий.

Первая из таких стратегий (она оптимальна по затратам электроэнергии) состоит в перемещении поезда путем подачи общей команды несколько раз, пока поезд №1 не подойдет к ближайшему пустому узлу, где он может переждать до подхода места, где он должен стоять (то есть позиции №0, в которой стоит поезд №6.

Вторая стратегия (она оптимальна по затраченному времени) состоит в перемещении поезда №1 и одновременно поезда №6 к ближайшему узлу перегона (позиция 27), причем первый поезд достигнет ее раньше и его можно поместить в тупик (позиции 28) для ожидания подхода поезда №6. Таким образом, позиции поездов №1 и №6 поменяются местами. Аналогично можно поменять местами позиции других поездов.

При решении задачи выбора частной матрицы на каждом шаге, выбирается та из них, которая быстрее сближает позиции, либо выполняет перемещение с меньшими затратами, в зависимости от выбранного критерия.