5.3. Моделирование влияния повышения квалификации машинистов локомотивного депо на количество брака в их работе

В данном подразделе излагается одна из моделей, разработанных кандидатом технических наук Кударовым Русланом С., учеником профессора Герасименко П. В. [25].

Здесь проведено моделирование влияния курсов повышения квалификации машинистов локомотивного депо на количество брака в их работе. Моделирование выполнялось в виде регрессионной зависимости количества брака в работе машинистов от их образования, учреждения курсов повышения квалификации и количества лет после прохождения курсов повышения квалификации. Для вычисления оценок коэффициентов регрессии использовался метод максимального правдоподобия.

По экспериментальным данным построена и оценена регрессионная модель количества брака в работе машинистов одного из локомотивных депо Октябрьской железной дороги. Показано, что разработанную регрессионную модель можно использовать для определения количества машинистов при планировании курсов повышения квалификаций.

В современных рыночных условиях транспортной системы России особое внимание руководителей железнодорожных предприятий уделено профессиональной подготовке персонала занятого в эксплуатации подвижного состава. Стремление к увеличению объемов грузо- и пассажирооборотов на железных дорогах и запуск в ближайшем будущем высокоскоростных поездов при необходимости обеспечения безопасного движения поездов предъявляют высокие требования к профессиональной подготовке машинистов. Одним из основных факторов, влияющих на профессиональную подготовку машинистов, являются курсы повышения квалификации.

Оценивание влияния курсов повышения квалификации машинистов на безопасность движения поездов предполагает разработку методик, базирующихся на методах статистического моделирования. В частности, в работе [25] предложена модель зависимости риска возникновения аварийной ситуации от квалификации и числа персонала. Разработанная модель предполагает непрерывность исследуемого показателя и нормальность его распределения, а также не учитывает его связи с учреждениями курсов повышения квалификации и количеством лет после прохождения курсов повышения квалификации. Сбор экспериментальных данных для предложенной модели требует учёта всех решений (действий) персонала за исследуемый промежуток времени.

Здесь в качестве показателя безопасности движения поездов рассматривается количество брака в работе машинистов локомотивного депо [26], данные по которому содержатся в книгах ф. РБУ-7 учета случаев брака, связанного с безопасностью движения поездов. Установлено, что эмпирическая гистограмма количества брака в работе машинистов хорошо аппроксимируется распределением вероятностей Пуассона, используемого, как правило, для описания распределения частот «редких» событий [27].

Оценивание согласия эмпирической гистограммы количества брака в работе машинистов одного из локомотивных депо с теоретической функцией распределения вероятностей закона Пуассона и плотностью нормального закона (где – случайная величина количества случаев брака в работе машинистов за 5 лет) осуществлено с помощью критерия хи-квадрат. Поскольку расчетное значение 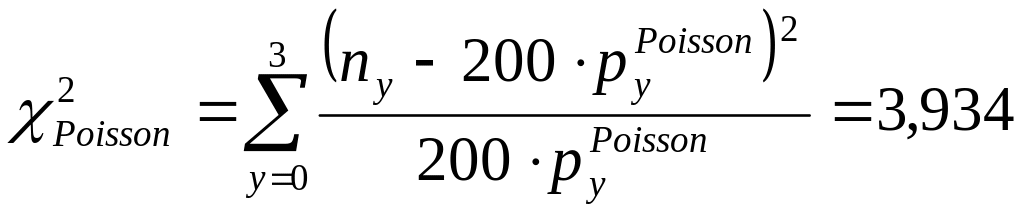^* меньше табличного и 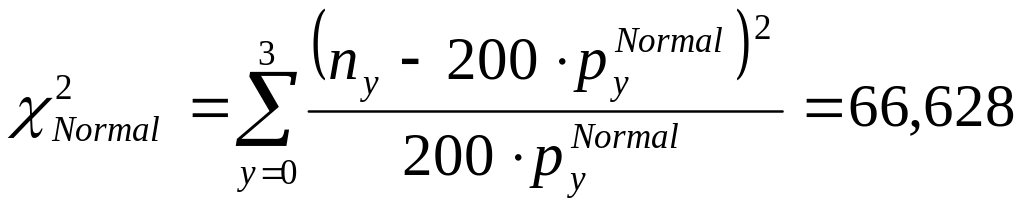^* больше табличного , то признается согласие эмпирической гистограммы количества брака в работе машинистов с распределением вероятностей Пуассона на уровне статистической значимости , и отклоняется предположение о нормальности распределения количества брака в работе машинистов.

Работа направлена на моделирование зависимости количества брака в работе машинистов локомотивного депо от учреждения курсов повышения квалификации и количества лет после прохождения курсов повышения квалификации.

При моделировании влияния курсов повышения квалификации машинистов локомотивного депо на количество брака в их работе в качестве показателей курсов повышения квалификации выступают:

1) учреждение курсов повышения квалификации

2) количество лет после похождения курсов повышения квалификации.

Кроме того, поскольку на результаты прохождения курсов повышения квалификации оказывает влияние уровень образования машинистов, в моделируемой зависимости учитывается показатель образования машиниста (уровень образования – образовательный ценз).

При вводе в модель неколичественных переменных «учреждение курсов повышения квалификации» и «уровень образования» используется техника фиктивных переменных [26]. При этом согласно [27] включены нулевые уровни неколичественных факторов («контроли»), т.е. при построении модели обследованию подлежат также машинисты, не проходившие курсы повышения квалификации и не получившие специализированного образования в соответствующем учебном заведении.

Изучаемый показатель безопасности движения поездов при построении моделируемой зависимости не дифференцируется по степени тяжести.

Таким образом, моделирование влияния курсов повышения квалификации (КПК) машинистов локомотивного депо на количество брака в их работе выполняется в виде функции регрессии

,

где – наблюдённое количество брака в работе -го машиниста за определенный временной период на текущий момент; – теоретическое значение количества брака в работе -го машиниста, вычисленное в зависимости от его образования, учреждения курсов повышения квалификации и количества лет после прохождения курсов повышения квалификации; – переменная принимающая значение 1, если -й машинист имеет -й уровень образования (начальное профессиональное, среднее профессиональное или высшее профессиональное образование), и 0, если он имеет общее образование [28]; – переменная принимающая значение 1, если -й машинист проходил курсы повышения квалификации в -м заведении, и 0, если он не проходил курсов повышения квалификации; – количество лет после прохождения курсов повышения квалификации -м машинистом на текущий момент.

Теоретические значения количества брака в работе машинистов задаются в следующем виде:

где , , …, , …, , , …, , …, – искомые оценки регрессионных параметров, которые вычисляются методом максимального правдоподобия в предположении Пуассоновского распределения количества брака в работе машинистов.

Для минимизации дисперсии оценок регрессионных параметров и с учётом специфики моделируемой зависимости, экспериментальные значения количества лет после прохождения курсов повышения квалификации преобразовываются по формуле

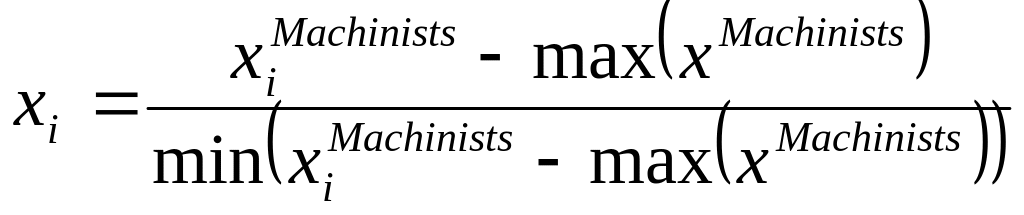. (1)

Проверка на адекватность статистической модели, построенной по имеющейся выборке, осуществляется по критерию хи-квадрат [27] с помощью вычисления девиации, которая при Пуассоновском распределении имеет вид

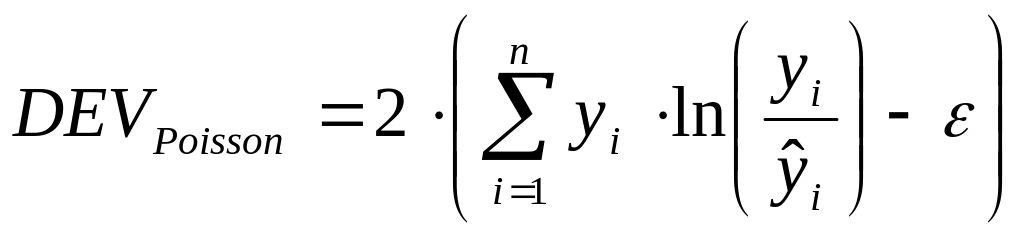, где .

Пусть введён показатель эффективности курсов повышения квалификации

, (2)

где – суммарное количество брака в работе обследуемых машинистов за исследуемый период до прохождения курсов повышения квалификации;

– суммарное количество брака в работе обследуемых машинистов после прохождения курсов повышения квалификации машинистами;

Тогда с помощью разработанной регрессионной модели можно рассчитывать значения эффективности курсов повышения квалификации на будущий краткосрочный период не более 1 года. При этом

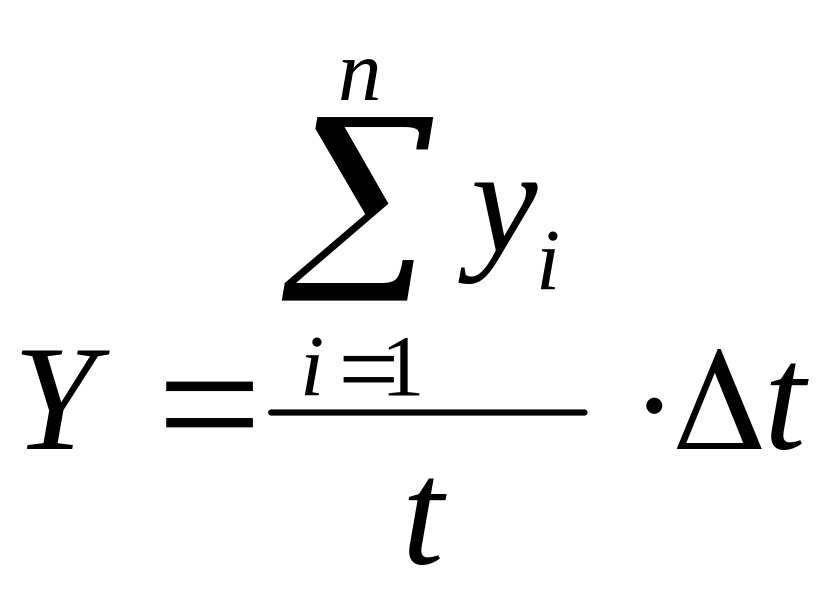и

.

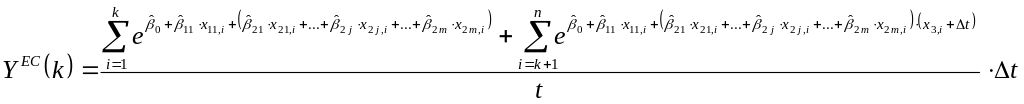Задавая пороговое значение показателя эффективности курсов повышения квалификации можно устанавливать количество машинистов при составлении планов прохождения курсов повышения квалификации на следующий год.

Использование показателя эффективности курсов повышения квалификации (2) предполагает, что условия и режим работы машинистов остаются одинаковыми в течение одного года, а также существенного влияния на количество брака в работе машинистов в течение одного года не оказывают

1) изменение технических показателей подвижного состава;

2) психофизиологическое состояние машинистов;

3) приобретенный за исследуемый период опыт.

В принятых предположениях значения показателя эффективности курсов повышения квалификации лежат в пределах . Максимальное значение эффективности курсов повышения квалификации достигается, когда количество брака в работе обследуемых машинистов после прохождения курсов повышения квалификации равно 0. Если количество брака в работе машинистов после прохождения курсов повышения квалификации не уменьшилось, то эффективность курсов повышения квалификации равно 0.

В работе излагается оценивание влияния курсов повышения квалификации на количество брака в работе машинистов одного из локомотивных депо Октябрьской железной дороги.

В соответствии с классификацией нарушений безопасности движения в поездной и маневровой работе на железных дорогах России в качестве брака в работе машинистов локомотивного депо рассматриваются не устраненные машинистами неисправности локомотива, вызвавшие задержку в пассажирском движении на 1 час и больше или в результате которых потребовался вспомогательный локомотив для пассажирского поезда.

Поскольку целью построения модели не является использования её для сравнения результатов обучения в различных учреждениях курсов повышения квалификации или образовательных учреждениях, то при планировании экспериментального сбора исследуемых показателей целесообразным являлось минимизировать количество (смешивание) уровней переменных «учреждение курсов повышения квалификации» и «уровень образования» [29].

Всевозможные комбинации учтенных в исследовании уровней образования и учреждений курсов повышения квалификации обследуемых машинистов сведены в таблицу 1.

Таблица 1. Уровни образования и учреждений КПК

	Не проходил курсов повышения квалификации	Учреждение курсов повышения квалификации
		Учебно-подготовительный центр	Учебное заведение
Общее образование
Начальное профессиональное, среднее профессиональное, высшее профессиональное

Вычисление минимального необходимого количества обследуемых машинистов осуществлялось по формуле, определяющей необходимое количество наблюдений для установления Пуассоновского закона распределения:

,

где – минимальное необходимое количество наблюдений на каждый уровень сочетания неколичественных факторов; – предполагаемое значение интенсивности брака в работе машинистов; – исследуемый период времени; – табулированный параметр, зависящий от величины и ; – доверительная вероятность; – относительная предельная ошибка; – табулированный параметр, зависящий от величины и .

На уровне статистической значимости , при априори заданном среднем количестве брака в работе машинистов локомотивного депо за период работы лет расчетное и . Поэтому для оценивания искомых параметров моделируемой зависимости обследовано 84 машиниста со стажем более 5 лет.

На каждому уровне сочетания неколичественных факторов расчетные значения статистики хи-квадрат меньше соответствующего табличного , что подтверждает Пуассоновость условного распределения количества брака в работе машинистов.

Преобразованные по соотношению (1) экспериментальные значения количества лет после прохождения курсов повышения квалификации для обследуемых машинистов представлены в таблице 2.

Таблица 2. Преобразованные значения количества лет после прохождения квалификации

Экспериментальные значения	5 лет	6 лет	7 лет	8 лет	9 лет	10 лет	11 лет	12 лет	13 лет	14 лет	15 лет
Значения вводимые в модель	1	0,9	0,8	0,7	0,6	0,5	0,4	0,3	0,2	0,1	0

Оценки регрессионных параметров для имеющейся выборки вычислены в Excel методом Ньютона с точность до на 6-й итерации и представляют собой вектор .

Вычисленные оценки коэффициентов регрессии позволили записать искомые функции регрессии для каждого уровня сочетания образования и учреждений курсов повышения квалификации (таблица 3).

Таблица 3. Регрессионные зависимости брака в работе машинистов от количества лет после прохождения КПК на всех уровнях образования и учреждений КПК

	Общее образование	Начальное профессиональное, среднее профессиональное, высшее профессиональное
Не проходил КПК
УПЦ
ПГУПС, СПбТЖТ

Достаточно близкое к нулю значение девиации свидетельствует об адекватности построенной модели зависимости количества брака в работе машинистов обследуемого депо от их образовании, учреждении курсов повышения квалификации и количества лет после прохождения курсов повышения квалификации. Использование критерия хи-квадрат позволило установить, что построенная модель является статистически значимой на уровне , поскольку .

Для верификации построенной регрессионной зависимости обследованы оставшиеся 45 машинистов обследуемого локомотивного депо, имеющих профессиональное образование и проходившие курсы повышения квалификации в учебно-подготовительных центрах или учебных заведениях. По критерию хи-квадрат подтверждена достоверность исследования на уровне значимости , т. к. .

Вычисленные значения показателя эффективности курсов повышения квалификации на следующий год работы приведены в таблице 4.

Таблица 4. Прогнозные значения показателя эффективности КПК

	Машинисты, допустившие 4 брака за последние 5 лет	Машинисты, допустившие 3 и 4 брака за последние 5 лет	Машинисты, допустившие 2, 3 и 4 брака за последние 5 лет
Предполагаемое количество машинистов при составлении планов КПК	2	5	16
Прогнозируемое количество брака в работе обследуемых машинистов на следующий год	13	12	10
Прогнозные значения показателя эффективность КПК	0,03	0,09	0,24

С учетом заданного значения показателя эффективности курсов повышения квалификации предполагаемое количество машинистов при составлении планов курсов повышения квалификации равно 6.

Итак, здесь проведено моделирование влияния курсов повышения квалификации на количество брака в работе машинистов локомотивного депо. Моделирование выполнено в виде регрессионной зависимости количества брака в работе машинистов от их образования, учреждения курсов повышения квалификации и количества лет после прохождения курсов повышения квалификации. Вычисление оценок коэффициентов регрессии произведено методом максимального правдоподобия, а оценивание качества функции регрессии – по критерию хи-квадрат с помощью вычисления девиации.

По экспериментальным данным построена и оценена регрессионная модель количества брака одного из локомотивных депо Октябрьской железной дороги. Установлена статистическая значимость разработанной модели и достоверность проведенного исследования на уровне значимости .

Показано, что использование разработанной регрессионной модели позволяет устанавливать количество машинистов при планировании курсов повышения квалификаций.