0. 4.5. Имитационная модель системы массового обслуживания

1. Сущность метода имитационного моделирования состоит в имитации объекта (системы, процесса и т. д.) с помощью определенных математических, логических, программных и технических приемов и средств.

Применение метода имитационного моделирования к системам массового обслуживания состоит в моделировании процесса поступления заявок в систему, в моделировании распределения заявок по обслуживающим устройствам, моделировании процесса обслуживания, накопления результатов и обработки результатов для получения содержательных выводов о характеристиках системы (среднего числа заявок в очереди, среднего числа занятых устройств, вероятности отказа и т. д.).

Реализация имитационных моделей в настоящее время осуществляется главным образом на компьютерах и с помощью математических пакетов программ, установленных на этих компьютерах.

Для более четкого и ясного представления о характере имитационных моделей систем массового обслуживания, а также для того, чтобы иметь возможность обсуждать проблемы, связанные с имитационным моделированием таких систем, рассмотрим простейшую систему массового обслуживания с отказами с n обслуживающих устройств и со случайными моментами поступления заявок и случайными временами обслуживания заявок.

Составим имитационную модель такой системы для реализации на компьютерах с целью получения характеристик системы.

Введем следующие обозначения:

t_j – время освобождения j-го устройства от обслуживания;

t_з – время занятости устройства обслуживанием (случайная величина);

T_k – время поступления k-й заявки;

Т_кон – время окончания опыта;

τ_k – интервал времени между двумя соседними заявками (случайная величина);

N – общее число опытов, например, рабочих дней и т. д.;

j – индекс номера опыта;

k – индекс номера заявки;

i – индекс номера обслуживающего устройства;

n – общее число обслуживающих устройств.

Система не предусматривает очереди, и заявки, заставшие все устройства обслуживания занятыми, получают отказ. Для определения приближенных значений характеристик системы в модели предусмотрен подсчет числа выполненных заявок и числа заявок, получивших отказ.

Блок-схема модели системы представлена на рис. 4.5.1. Рассмотрим, как работает алгоритм модели.

В блоке 1(номера блоков указаны цифрами справа, сверху, реже слева от блока) задается номер опыта (например, номер рабочего дня). В блоке 2 задаются начальные условия каждого опыта: первая заявка поступает в момент 0: Т₁ = 0; все устройства обслуживания свободны: t₁= t₂=…= t_n=0; первая заявка имеет номер 1: k=1.

В блоке 3 проверяется условие, попала ли заявка со временем прихода T_k в рамки окончания опыта, т. е. условие T_k<T_кон. Если попала, то в блоке 5 начинается проверка занятости устройств обслуживания; если не попала, то в блоке 4 организуется процедура завершения опыта.

В блоке 7 осуществляется проверка условия, свободно ли i-е устройство обслуживания к моменту поступления k-й заявки T_k.

Если i-е устройство обслуживания свободно, то заявка поступает на обслуживание: в блоке 10 моделируется случайное время занятости устройства t_з, затем в блоке 12 формируется новое время освобождения i-го устройства от обслуживания:

t_i =T_k+ t_з и в блоке 14 к счетчику числа выполненных заявок добавляется единица.

Таким образом, либо в блоке 13, либо в блоке 14 завершается присутствие k-й заявки в СМО: заявка либо будет обслужена, либо получит отказ, и необходимо приступить к рассмотрению следующей заявки.

В блоке 15 моделируется случайное значение интервала времени τ_k между двумя очередными заявками; в блоке 16 формируется новое значение времени поступления очередной заявки: T_k+1= T_k+ τ_k, а в блоке 17 – номер новой заявки и управление передается блоку 3 для рассмотрения этой заявки.

Рассмотрим теперь процедуру завершения моделирования. В блоке 6 увеличивается на единицу номер опыта (например, номер рабочего дня), а в блоке 8 проверяется условие, является ли этот опыт последним: если опыты еще не завершены («да» в блоке 8), то очередной опыт моделируется (управление передается блоку 2), если же опыты завершены («нет» в блоке 8), то далее в блоке 18 осуществляется обработка результатов эксперимента.

Под обработкой результатов моделирования понимается получение приближённых значений характеристик СМО. Например, в рассмотренной здесь модели нетрудно получить следующие характеристики СМО с отказами:

- среднее число обслуженных заявок как среднее арифметическое выполненных заявок, накопленных в счетчике заявок, по всем N опытам;

- среднее число отказов как среднее арифметическое отказов, накопленных в счетчике отказов, по всем N опытам;

- вероятность отказа как среднее арифметическое отношений числа отказов ко всем заявкам, поступившим в систему (сумма значений двух вышеуказанных счетчиков), по всем N опытам.

Особенностью и достоинством имитационных моделей СМО по сравнению с аналитическими методами, рассмотренными в предыдущей главе, является то, что в них могут быть рассмотрены СМО с любыми законами распределения времен поступления заявок и любыми законами времен обслуживания, достаточно лишь смоделировать эти величины в соответствии с их законами в блоках 10, 12, 15, 16. На практике, для получения этих законов необходимо организовывать статистическое экспериментирование для получения значений величин времен поступления заявок и времен обслуживания («хронометраж»).

Недостатком имитационных моделей является то, что они могут быть реализованы лишь при конкретных числовых значениях всех величин, входящих в моделируемую систему, и для исследования моделей с меняющимися в некотором диапазоне параметрами (например, число устройств обслуживания n) необходимо достаточно объемное по времени моделирование.

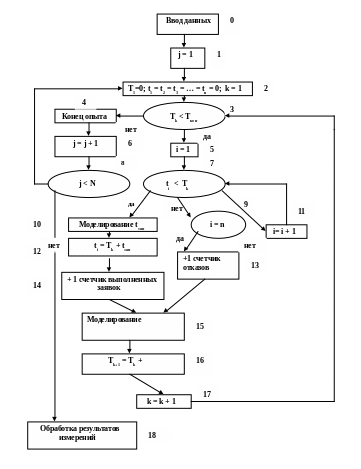
Рис. 4.5.1. Блок-схема модели системы массового обслуживания

5. НЕКОТОРЫЕ МОДЕЛИ СИСТЕМ

ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

5.1. Модель оптимального по стоимости управления вагонами с учетом

иностранных вагонов и вагонов различных форм собственности

В данном разделе излагаются результаты моделирования процессов регулирования вагонопотоков с учетом вагонов различных форм собственности и различных стран. Эти результаты получены профессионалами – железнодорожниками высокого уровня Ковалевым В.И., Елисеевым С.Ю, Осьмининым А.Т. и математиком специалистом по математическому моделированию Дегтяревым В.Г. Результаты изложены в многочисленных публикациях, основными из которых являются статьи в Вестнике ВНИИЖТ [10], в Известиях Международной Академии наук высшей школы [11] и в учебном пособии [12].

Использование математических методов для моделирования и управления вагонопотоками на советских и российских железных дорогах имеет уже почти полувековую историю [13].

В настоящее время основными методами решения проблемы оптимального регулирования вагонопотоков являются методы линейного программирования, вообще, и транспортная задача линейного программирования, в частности. Эти методы положены в основу задействованных или разрабатываемых автоматизированных систем управления вагонным парком [14].

Особенностью нынешнего периода использования вагонного парка на территории Российских железных дорог (РЖД) является наличие на РЖД значительного количества вагонов других государств. Правила эксплуатации, учета и взаиморасчетов за пользование такими вагонами определены межгосударственными соглашениями между железнодорожными ведомствами стран СНГ и Балтии [15]. Естественно, что решение проблемы оптимального регулирования вагонопотоков не может быть выполнено без учета этой достаточно многочисленной категории вагонов. В монографии Е.М. Тишкина [14] обсуждаются и решаются некоторые частные задачи, связанные с использованием иностранных вагонов, однако, при формулировке задач регулирования порожних вагонопотоков [13, с. 201-206] этот учет практически не осуществляется.

В более поздних разработках сотрудников ВНИИЖТа [16, 17, 18], несмотря на значительное продвижение в направлении квалифицированного решения проблемы регулирования вагонопотоков на современном уровне, также не производится учет наличия парка иностранных вагонов.

Между тем, с экономической точки зрения проблема стоит достаточно серьезно. Из источника [19] следует, что в 2000 году на территориях других государств находилось 37582 российских вагона (наиболее крупными «держателями» вагонов являлись Украина (11640), Казахстан (7665), Белоруссия (4243), Эстония (4240), Латвия (3432) и т.д.). С другой стороны, в том же 2000 году на территории РЖД находилось 26115 вагонов других государств (наибольшее количество вагонов относилось к вагонам Казахстана (9204), Украины (7050), Белоруссии (4524), Узбекистана (1760) и т.д.). Отсюда видно, что в 2000 году общий баланс в пользу России и это отражается в плате за использование вагонов (по данным [19] сальдо 196099,3 тыс. швейцарских франков в пользу России). Однако, по материалам совещаний в МГТС РФ, уже в 2001 году баланс был не в пользу России.

Вывод, который отсюда может быть сделан, состоит в том, что иностранные вагоны невыгодно после их разгрузки держать в резерве, так как за каждый день задержки вагона государству – владельцу необходимо платить штраф, невыгодно также их загружать и отправлять в произвольном направлении, так как в этом случае также увеличивается срок задержки и, как следствие, увеличивается штраф. Экономически наиболее разумным будет решение: загружать и отправлять в «попутном» направлении. Термин в «попутном» направлении в данном случае означает, что, во-первых, вагон действительно приближается к межгосударственному пункту передачи вагона государству-владельцу и, во-вторых, что доход, получаемый от использования вагона для доставки груза, превышает эксплуатационные расходы по перемещению вагона с учетом штрафа за задержку вагона.

В последнее время на территории РЖД все более и более увеличивается парк российских вагонов других, кроме МГТС, форм собственности (компаний-операторов, экспедиторских компаний крупных фирм и т.д.).

Относительно этих вагонов положение еще более сложное, чем с иностранными вагонами. Дело в том, что нет общероссийского типового соглашения между МПС и фирмами-владельцами вагонов. Соглашения, как правило, заключаются между дорогами, входящими в состав МПС, и владельцами вагонов и эти соглашения могут существенно отличатся одно от другого. Например, там вообще может отсутствовать пункт о возможном использовании вагонов службами МПС, поэтому в априорной постановке задачи о регулировании вагонопотоков может присутствовать такая характеристика, как вероятность использования вагона службами МПС. В дальнейшем будем именовать подобные вагоны как вагоны «других форм собственности».

Насколько нам известно, проблема регулирования вагонопотоков с учетом такого подразделения вагонов в научной литературе ранее не обсуждалось.

Очевидно, разумно в отношении этих вагонов применять такой же подход, как и в отношении иностранных вагонов.

Ниже дается постановка и решение проблемы оптимального регулирования вагонопотоков с учетом вагонов трех форм собственности: МПС России, иностранных и других форм собственности. Поскольку целесообразность использования «чужого» вагона оценивается полезностью перевозки на нем груза в «попутном» направлении, то задача принимает вид задачи двойной оптимизации: оптимизация порожнего пробега вагонов и оптимизация развоза груза. Это типично для оптимального регулирования вагонопотоков, где часто применяются методы многократной оптимизации [20].