Р ис.1.59. Фчх схемы, приведенной на рис.1.57,

при R₁=3R₂.

Используя приведенную методику, нетрудно вывести формулы коэффициентов передачи более сложных цепей, в том числе цепей с двумя конденсаторами.

Умение получать выражения для коэффициентов передачи RC-цепей в комплексной форме можно использовать для нахождения переходных характеристик. Для этого в выражении для сопротивления емкости синусоидальному току необходимо заменить jω на оператор р. При этом получаем операторное выражение для сопротивления емкости . Законы Ома и Кирхгофа можно также выразить в операторной форме, заменяя İ на Ι(p) и на U(p). Используя эти замены, можно найти коэффициент передачи RC-цепи также в операторной форме. Сделаем это для простейшей интегрирующей RC-цепочки (рис.1.48). Запишем уравнения: , . Отсюда , где τ=RC.

Для простейшей дифференцирующей RC-цепочки получим: , где τ=RC.

Для нахождения переходных характеристик теперь достаточно от операторной формы К(р) перейти к оригиналу К(t). Таблицы формул оригиналов и их операторных выражений для типовых случаев приводятся в учебниках [ ]. Таким образом, если возникают трудности в построении переходных характеристик RC-цепей, то можно используя операторный метод и таблицы перехода от операторной формы к оригиналам, получить выражения переходных характеристик RC-цепей.

Вопросы и задачи для самопроверки:

1. Может ли через конденсатор протекать переменный ток?

2. Какое напряжение возникнет на конденсаторе, если его подсоединить к источнику синусоидального тока?

3. Чему равно сопротивление конденсатора протекающему по нему синусоидальному току?

4. Дайте определение амплитудно-частотной и фазочастотной характеристикам?

5. Как использовать законы Кирхгофа для RC-цепи, находящейся под воздействием синусоидального напряжения?

6. Как определить ток, протекающий через конденсатор, если известно приложенное к нему синусоидальное напряжение?

7. Как определить коэффициент передачи цепи при

= 0?

8. Как определить коэффициент передачи цепи при

= ∞?

9. Как определяются верхняя и нижняя граничные частоты в RC - цепях?

10. Чему может быть равен максимальный фазовый сдвиг между входным и выходным напряжениями в интегрирующих и дифференцирующих цепях?

11. Как влияют на АЧХ интегрирующей RC - цепи сопротивление генератора и паразитная емкость нагрузки?

12. Как изменится АЧХ дифференцирующей цепочки из-за влияния сопротивления генератора?

13. Как изменится АЧХ дифференцирующей цепочки из-за влияния паразитной емкости нагрузки?

14. Нарисуйте АЧХ следующих цепочек:

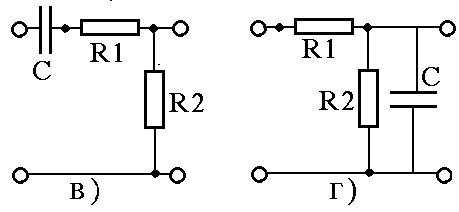
15. Нарисуйте ФЧХ для цепей, приведенных в предыдущем вопросе.

1.6. RLC–цепи при синусоидальном сигнале.

Рассмотрим процессы, происходящие в катушке индуктивности, при воздействии на нее синусоидального напряжения (рис.1.60, Е₀sint – идеальный источник напряжения).

Рис.1.60. Катушка индуктивности, находящаяся под воздействием источника синусоидального напряжения.

При положительной полуволне напряжения происходит увеличение тока, протекающего через катушку индуктивности после момента t₁ (рис.1.61) в указанном на рисунке направлении (рис.1.60). До этого момента в катушке была накоплена магнитная энергия, которая вызывала ток, текущий в противоположном направлении. После момента t₁ в катушке постепенно накапливается магнитная энергия, причем вектор магнитной индукции меняется на 180^о. Рост тока прекратится, когда синусоидальное напряжение генератора станет равным нулю (момент времени t₂). Но ток при этом не прекратится, т.к. в катушке была накоплена магнитная энергия.

Рис.1.61. Синусоидальное напряжение и ток в катушке

индуктивности.

Ток будет лишь уменьшаться, т.к. на катушку начинает действовать напряжение противоположной полярности. При достижении момента t₃, когда напряжение генератора будет минимально, ток упадет до нуля. При этом магнитная энергия также станет равной нулю. Но при t₃<t<t₄ на катушку продолжает действовать отрицательное напряжение, которое приведет к появлению тока, противоположному указанному на рисунке направлению. В теории электрических цепей показано, что при воздействии на катушку индуктивности сигнала от генератора синусоидальных напряжений, ток также будет изменяться по синусоидальному закону при этом, как видно из приведенного рисунка, напряжение будет опережать ток в катушке индуктивности на 90^о.

Из физической сути происходящих в катушке изменений, очевидно, что накапливаемая в катушке индуктивности магнитная энергия препятствуют изменению тока, причем, чем быстрее будет изменяться напряжение, тем большим будет сопротивление катушки этим изменениям. В тоже время магнитная энергия, накапливаемая в катушке и препятствующая изменению тока, будет тем больше, чем больше величина индуктивности. Из этих соображений понятна формула, которая выводится в теории электрических цепей: Z_L=jωL, где Z_L – сопротивление индуктивности при синусоидальном сигнале,

j — мнимая единица, показывающая, что напряжение на катушке индуктивности опережает ток на 90^о, ω – круговая частота синусоидального тока. Как и в случае для конденсатора, катушку индуктивности можно считать линейным элементом, а при расчете цепей, содержащих этот компонент использовать законы Ома и Кирхгофа. Если катушка индуктивности имеет магнитный сердечник, то при достаточно больших токах намагничивания возникает гистерезис в магнитном материале и катушку уже нельзя считать линейным элементом.

Используя полученную формулу нетрудно рассчитать цепи, содержащие катушку индуктивности, при воздействии на них синусоидального напряжения. Рассчитаем АЧХ и ФЧХ ин тегрирующей RL–цепи, приведенной на рис.1.62.

Рис.1.62. Интегрирующая RL–цепь.

Ток в цепи равен , а напряжение на выходе будет равно: .

Таким образом, коэффициент передачи цепи равен

Если сравнить полученную формулу с формулой для коэффициента передачи интегрирующей RC–цепи (4), то, как видим, формулы идентичны. Отличие состоит лишь в том, что постоянная времени данной цепи равна L/R. Поскольку коэффициенты передачи идентичны, то идентичны будут АЧХ и ФЧХ данной RL–цепи и интегрирующей RC–цепи. Также будут идентичны АЧХ и ФЧХ дифференцирующих RL и RC–цепей.

Например, если в случае интегрирующей RL-цепочки R=100 Ом, L=10 мкГн, то =(10*10^-6/100 ) с=10^-7 с=0,1 мкс, а

f_В Гц≈1,6 МГц.

Рассмотрим RLC–цепь (рис.1.63) при воздействии синусоидального напряжения.

Рис.1.63. RLC–цепь – звено фильтра нижних частот.

Ток в цепи можно определить по формуле: .

Напряжение на выходе будет равно .

Отсюда коэффициент передачи равен .

Для нахождения АЧХ найдем модуль коэффициента

передачи:

. (12)

Из формулы (12) видно, что при w=0 ½ (jw)½=1.

В подкоренном выражении знаменателя формулы (12) есть два слагаемых, одно из которых при определенных значениях w становится близким к нулю. Докажем, что при этом ½ (jw)½ может стать больше 1. Функция ½ (jw)½имеет максимум при минимальном значении подкоренного выражения в знаменателе выражения (12). Выразим квадрат знаменателя A через переменную x= . Отсюда A(x) = +x . Продифференцировав A(x) по x и приравняв производную нулю, получим: -2(1-xLC)LC+ =0 или 2x .

При условии x=0 и w=0, т.е. максимум функции ½ (jw)½ находится на частоте w=0. Если 2LC , то x= , а = . Отсюда ½ (j )½= . При выбранных L и C ½ (j )½>1 или½ (j )½<1, в зависимости от значения R.

Например, если L=0,5 мГн, С=1 нФ, то, в зависимости от значения R, возможны различные случаи. Положим R=1 кОм. В этом случае, как показывает анализ, выброса в АЧХ не возникает, а f_В=224,5 Гц. При R>1 кОм выброса также не будет.

В случае, если R=10 Ом, на частоте f₀=224,5 Гц возникает большой выброс в АЧХ, а именно =70,7.

В этом случае в RLC-цепи возникает резонанс. Если при этом подать на вход импульсный сигнал, то на выходе получатся затухающие колебания большой длительности.

И з формулы (12) видно, что при R=0 ½K(jw₀)½=¥, что соответствует возбуждению в схеме незатухающих колебаний с частотой w₀=1/ . На рис.1.64 приведены зависимости ½ (jw)½ от частоты при различных R.

Рис.1.64. АЧХ RLC–звена фильтра нижних частот.

Приведенная на рис.1.63 RLC–цепь обычно используется в качестве звена фильтра нижних частот (фильтра, который пропускает только низкие частоты и подавляет высокие).