Р ис.1.2.Электрическая цепь из батареи, проводов и лампочки.

Для идеального случая (пренебрегаем внутренним сопротивлением батарейки и сопротивлением проводов) схема цепи, изображенной на рис.1.2, представлена на рис.1.3, где введены следующие обозначения: Е_Б – э.д.с. батарейки, величина которой равна разности потенциалов, создаваемых на ее внешних зажимах, R_Л – сопротивление нити накала электрической лампочки. Разность потенциалов или напряжение на лампочке U_Л равны э.д.с. батарейки Е_Б=U_Л, причем напряжение можно измерить вольтметром. Через лампочку потечет ток. Силу тока через лампочку обозначим I и напомним, что сила тока равна количеству электрического заряда, протекающего через какое-то сечение проводника за единицу времени. Ток измеряется в амперах (А) амперметром или миллиамперметром (микроамперметром). Известно, что силу тока I на участке цепи, обладающим каким-то сопротивлением R, можно определить по закону Ома: I=U/R, где сопротивление измеряется в Омах. Таким образом, для рассматриваемой цепи получаем:

I_Л= U_Л/ R_Л=Е_Б/R_Л. Например, если Е_Б=5В, а R=25 Ом, то сила тока получается равной: I=5/25=0,2А=200 мА (миллиампер).

Р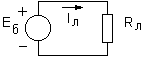 ис.1.3.Идеализированная схема цепи,

состоящей из батарейки, проводов и лампочки.

Закон Ома изучается в школе, но иногда студенты путают связь между U, I и R. Чтобы избежать этого, можно использовать аналогию с течением реки, вытекающей из водохранилища. В этом случае напряжение в электрической цепи аналогично перепаду высот между уровнем воды в водохранилище и нижней точкой выбранного участка реки. Ток в электрической цепи аналогичен объему воды, протекающей в единицу времени через сечение реки. Очевидно, что чем больше перепад высот, тем больше скорость течения реки и больший объем текущей воды в единицу времени. Соответственно для электрической цепи, чем больше напряжение, т.е. разность потенциалов, тем больше ток.

Аналогия с течением реки помогает понять и смысл термина «сопротивление». Чем длиннее русло реки, чем оно уже, тем меньший объем воды протекает за единицу времени по реке при одинаковом перепаде высот. Соответственно, чем длиннее и тоньше провода, тем больше сопротивление проводов и меньшее количество электрического заряда протекает в электрической цепи за единицу времени при одинаковой э.д.с. источника.

Величина, обратно пропорциональная R, называется проводимостью G=1/R. С использованием этой величины закон Ома будет иметь вид: I=UG.

Аналогия с рекой помогает понять и законы Кирхгофа, знание которых необходимо для анализа электрических цепей.

Первый закон Кирхгофа гласит: алгебраическая сумма токов, протекающих через узел цепи, равна нулю. По-другому этот закон можно сформулировать так: сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из этого узла. Этот закон иллюстрирует рис.1.4.

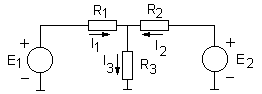
Рис.1.4. Пример, иллюстрирующий первый закон

Кирхгофа.

Для схемы, приведенной на рис.1.4: I₃=I₁+I₂. Очевидна аналогия: сколько воды в единицу времени пройдет через сечение русел каждой из двух сливающихся рек, столько же воды будет протекать в единицу времени через сечение русла реки после слияния двух рек.

Второй закон Кирхгофа гласит, что алгебраическая сумма э.д.с. в замкнутом контуре электрической цепи равна алгебраической сумме падений напряжений на сопротивлениях в этой же цепи. Проиллюстрируем выполнение этого закона на примере цепи, состоящей из батарейки, проводов и лампочки, изображенной на рис.1.2. По сравнению с идеальным случаем учтем внутреннее сопротивление батарейки и сопротивление проводов (рис.1.5).

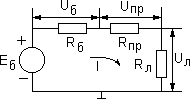
Рис.1.5. Полная схема цепи, состоящей из батарейки,

проводов и лампочки.

Для приведенной на рис.1.5 схемы это означает, что E_Б=U_Б+U_ПР+U_Л, где E_Б – э.д.с. батарейки, U_Б – падение напряжения на внутреннем сопротивлении батарейки R_Б, U_ПР – падение напряжения на сопротивлении проводов R_ПР, U_Л – падение напряжения на сопротивлении нити накала R_Л. С учетом закона Ома получаем: Е_Б=I(R_Б+R_ПР+R_Л).

Заметим, что максимальный ток, отдаваемый электрической батареей во внешнюю цепь, получается в режиме короткого замыкания, при котором R_ПР=R_Н=0, и он равен / R_Б. Если этого тока недостаточно для питания внешней цепи, то, казалось бы, его можно увеличить, если параллельно включить две идентичные батарейки с э.д.с. Е_Б1=Е_Б2 и R_Б1=R_Б2. В действительности всегда Е_Б1≠Е_Б2 и R_Б1≠R_Б2, и ток I. = Е , протекающий между батарейками, будет их разряжать. Срок службы батареек будет существенно меньше, чем гарантированно производителем.

И з второго закона Кирхгофа очевидно, что если два резистора с сопротивлениями R₁ и R₂ включить последовательно (рис.1.6а), то суммарное сопротивление этого последовательного сопротивление резисторов R_∑ будет равно сумме сопротивлений R_∑=R₁+R₂, т.к. ток, протекающий по сопротивлениям, будет одинаков, а падение напряжения на двух сопротивлениях будет равно сумме падений на каждом из них: E_Б=U₁+U₂=IR₁+IR₂=I(R₁+R₂)=IR_∑.

а) б)

Рис.1.6. а) последовательное включение сопротивлений,

б) параллельное включение сопротивлений.

Если два сопротивления включить параллельно друг другу (рис.1.6б), то, как следует из первого закона Кирхгофа, суммироваться будут не напряжения, а токи: I=I₁+I₂=E/R₁+E/R₂=E(1/R₁+1/R₂). Таким образом, если заменить два параллельно включенных сопротивления эквивалентным сопротивлением R_ЭКВ, то его величина должна обеспечивать одинаковый ток в цепи: I=E/R_ЭКВ=E(1/R₁+1/R₂). Отсюда 1/R_ЭКВ=1/R₁+1/R₂ или R_ЭКВ=R₁R₂/(R₁+R₂).

Следует отметить, что эквивалентное сопротивление при параллельном соединении двух сопротивлений получается меньше меньшего из них. Например, R₁=6 Ом, R₂=3 Ом, R_ЭКВ=(6*3)/(6+3)= 2 Ом.

Внутреннее сопротивление источника (генератора) электрической энергии характеризует его свойства. Различают два случая: источник постоянного напряжения и источник постоянного тока. Источник постоянного напряжения имеет внутреннее сопротивление обычно гораздо меньшее, чем сопротивление подключаемых к нему цепей. В идеальном источнике напряжения внутреннее сопротивление равно нулю, как и было нами предположено для схемы на рис.1.3. В идеальном источнике тока внутреннее сопротивление равно бесконечности. Для удобства расчетов в схемах возможна замена источников напряжения на источники тока и наоборот. Например, источник постоянного напряжения с э.д.с., равной E, и внутренним сопротивлением R_Г можно заменить источником тока с тем же внутренним сопротивлением и силой тока, равной E/R_Г (рис.1.7).

Р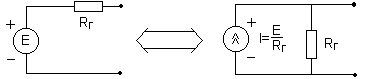 ис.1.7. Эквивалентные преобразования

источников напряжения и тока.

Убедимся в том, что преобразование генератора напряжения в генератор тока является эквивалентным, т.е. расчеты с использованием этих эквивалентных генераторов дают одинаковый результат. Пусть к этим генераторам подключено одинаковое сопротивление нагрузки R_Н (рис.1.8).

Рис.1.8. Схемы эквивалентных источников напряжения а)

и тока б) с одинаковым сопротивлением нагрузки.

Необходимо рассчитать ток в нагрузке. Для схемы с источником напряжения (рис.1.8а) одинаковый ток I_Н протекает по сопротивлениям R_Г и R_Н. По второму закону Кирхгофа Е=U_Rг+U_Rн, где U_Rг – падение напряжения на сопротивлении R_Г, U_Rн – падение напряжения на сопротивлении R_Н. По закону Ома: U_Rг=I_НR_Г, U_Н=I_НR_Н. Отсюда получим, что Е= I_Н(R_Г+R_Г) или .

Для схемы с источником тока (рис.1.8б) токи в сопротивлениях R_Г и R_Н будут разные. По первому закону Кирхгофа сумма этих токов равна току генератора , , или .

Оба тока, протекая по соответствующему сопротивлению, создают одинаковое напряжение U₁₀, определяемое формулой: U₁₀=I_ГR_Г=I_НR_Н= . Отсюда получаем I_НR_Н=Е-I_НR_Г или , что совпадает со значением тока, полученного выше. Таким образом, доказана эквивалентность преобразования источников напряжения и тока.

Р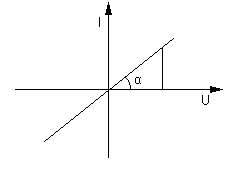 ассмотренные нами цепи и компоненты и их схемы называются линейными, т.к. для них зависимость тока от напряжения (вольтамперная характеристика) имеет линейный характер. Например, зависимость тока от приложенного напряжения к резистору линейна, как это показано на рис.1.9.

Рис.1.9. Вольтамперная характеристика сопротивления.

Тангенс угла наклона прямой на рис.1.9 по закону Ома обратно пропорционален величине сопротивления: tg=I/U=1/R.

Для линейных цепей удобно использовать принцип наложений или, как иногда его называют, принцип суперпозиций. Суть его заключается в том, что для нахождения каких-либо напряжений и токов в линейных цепях можно определять их последовательно сначала от одного источника э.д.с., затем от другого и т.д., а потом суммировать результаты этих расчетов. Также находятся напряжения и токи от источников тока, результаты также суммируются. Результаты расчетов напряжений или токов, обусловленные действием всех э.д.с., суммируются с аналогичными результатами, полученными из-за действия всех источников тока. При этих расчетах должно выполняться правило: если мы находим напряжение или ток от одного источника э.д.с. или источника тока, то все другие источники э.д.с. закорачиваются, а источники тока исключаются из схемы, и участок цепи при этом разрывается. Например, в рассмотренной нами схеме на рис.1.4 падение напряжения U₃ на сопротивлении R₃ можно вычислить следующим образом. Закорачиваем источник E₂, получаем следующую схему для расчета (рис.1.10а).

Рис.1.10. Эквивалентные схемы для расчета схемы, приведенной на рис.1.4, методом наложений.

Параллельное соединение сопротивлений R₂ и R₃ равно . Отсюда из второго закона Кирхгофа и закона Ома следует, что , а . Следовательно, _.

В схеме, приведенной на рис.1.10б, закорочен источник E₁. Параллельное соединение сопротивлений R₁ и R₃ равно . Отсюда из второго закона Кирхгофа и закона Ома следует, что , а . Следовательно, _.

Суммируя U₃^′ и U₃^″, получаем искомое напряжение

.

П риведем расчет схемы, в которой кроме источника э.д.с., используется источник (генератор) постоянного тока (рис.1.11а). Определим напряжение на сопротивлении .

Рис.1.11. а) Схема, содержащая источник э.д.с. – E_Б

и источник тока – I, и б) и в) эквивалентные схемы

для расчета ее методом наложений.

Из эквивалентной схемы (рис.1.11б), в которой источник тока исключен, получаем: .

Из эквивалентной схемы (рис.1.11в), в которой источник э.д.с. закорочен, получаем:

Суммируя и , получаем напряжение :

При расчете электрических цепей часто используют понятия коэффициента передачи. Коэффициент передачи напряжения определяют как отношение выходного напряжения к входному.

Допустим, имеется четырехполюсник (цепь, имеющая два входа и два выхода), приведенный на рис.1.12.

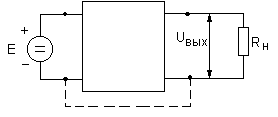
Рис.1.12. Схема четырехполюсника с входным источником э.д.с. и нагрузочным сопротивлением.

К входным клеммам четырехполюсника подключен источник э.д.с. К выходным клеммам четырехполюсника подключено нагрузочное сопротивление. Коэффициент передачи напряжения для данной цепи определяется следующим образом: K=U_ВЫХ/E.

В электронных цепях одна из входных клемм соединяется с одной из выходных клемм, как это показано пунктиром на рис. 1.12. Такая цепь называется трехполюсником. В электронных измерительных приборах и источниках питания общая с входом и выходом клемма обычно заземляется (соединяется с металлическими батареями отопления). В других электронных приборах (например, радиоприемниках, телевизорах, мобильных телефонах) общая клемма соединяется с одной из шин электропитания.

На основе трехполюсника можно выполнить делитель напряжений. Коэффициент передачи делителя напряжений, состоящего из двух резисторов (рис.1.13) можно определить, используя второй закон Кирхгофа: E=I(R₁+R₂), U_ВЫХ=IR₂: K=U_ВЫХ/E= R₂/(R₁+R₂). Например, если R₁=2 кОм, R₂=1 кОм, то К=1/(1+2)=0.33… Заметим, что К в пассивной цепи, с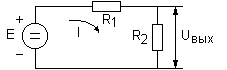 остоящей из резисторов, всегда меньше единицы.

Рис.1.13. Делитель напряжений, состоящий из двух

резисторов.