Практическое занятие №5 Элементарные преобразования матриц. Метод Гаусса

Напомним элементарные преобразования матрицы:

1. перестановка местами двух строк (столбцов) матрицы;

2. умножение всех элементов строки (столбца) матрицы на число, не равное нулю;

3. прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число, не равное нулю;

4. отбрасывание нулевой строки (столбца);

5. транспонирование матрицы.

Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Обозначение АВ.

При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такая матрица называется канонической: .

Пример 1. Привести к каноническому виду матрицу:

.

Решение.

Выполним элементарные преобразования:

Решение системы линейных уравнений методом Крамера и матричным способом удобно в случае решения систем 2-х или 3-х уравнений.

В случае решения систем большего числа уравнений и неизвестных проще использовать метод Гаусса, который состоит в последовательном исключении переменных.

Метод Гаусса отличается от методов Крамера и матричного еще и тем, что его можно применять при решении систем, имеющих уравнений и неизвестных. При решении систем линейных уравнений методом Гаусса удобно использовать запись в матричной форме.

Преобразования Гаусса удобно проводить, осуществляя элементарные преобразования не с самими уравнениями, а с матрицей их коэффициентов. В общем случае, если дана система из уравнений и неизвестных, матрица имеет вид:

.

Эта матрица называется расширенной матрицей системы.

Система, которая соответствует преобразованной матрице , эквивалентна исходной системе, т.е. имеет те же решения.

Замечание:

При решении систем методом Гаусса элементарные преобразования расширенной матрицы выполняются только со строками.

Рассмотрим возможные случаи на примерах.

Пример 1. Решить систему методом Гаусса .

Решение. Составим расширенную матрицу системы и выполним над ней элементарные преобразования (только по строкам):

(-7)

(-2)

 



(-3)

 .

Преобразованной матрице соответствует система:

или

Ответ: .

Пример 2. Решить систему методом Гаусса

Решение. Составим расширенную матрицу системы и выполним над ней элементарные преобразования (только по строкам):

(-2)

(-4)

(-1)

 

 .

Полученной матрице соответствует система, в которой третье уравнение имеет вид:

,

(неверно)  решений нет.

Ответ: решений нет

Выполнить задания:

1) Решить систему методом Гаусса:

а)

б)

в)

г)

д)

Раздел II. Аналитическая геометрия на плоскости Практическое занятие №6

Координаты точки. Расстояние между двумя точками. Деление отрезка в данном отношении. Площадь треугольника

Расстояние между двумя точками. Направление отрезка. Площадь треугольника

Рис. 1.

Случай 1. Пусть даны две точки тогда расстояние между ними равно:

(1)

Случай 2. Расстояние от начала координат до точки равно:

(2)

Направление отрезка АВ на плоскости ХОY определяется углом наклона этого отрезка к направлению оси ОХ (рис. 1).

Угол , образованный отрезком АВ и положительным направлением оси ОХ, равен:

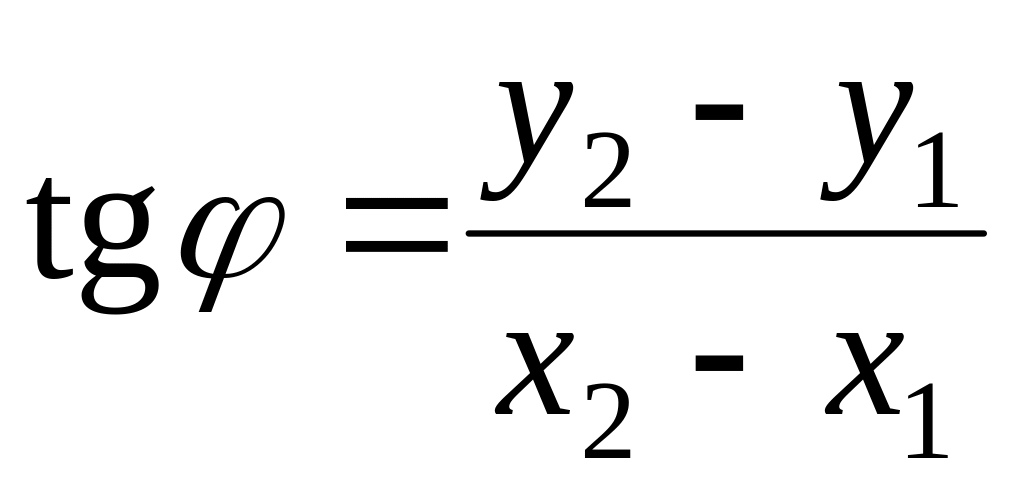. (3)

Если , то угол острый, если , то угол тупой.

Пусть даны координаты трех точек – вершин треугольника.

, , . Тогда площадь равна:

(4)

Утверждение.

Признаком того, что три различные точки лежат на одной прямой, может служить равенство нулю площади соответствующего треугольника:

, т.е. (5)

Пример 1. Под каким углом к положительному направлению оси Ох наклонен отрезок, соединяющий точки и ?

Решение.

По формуле (3) имеем:

.

Так как тупой угол, (по таблице).

Пример 2. Найти площадь треугольника, вершины которого находятся в точках: , , .

Решение.

По формуле (4) имеем:

.

Пример 3. Доказать, что три точки , , лежат на одной прямой.

Доказательство. Проверим, выполняется ли равенство (5):

в определителе второго порядка 1-й и 2-й столбцы пропорциональны с коэффициентом пропорциональности , следовательно, определитель равен нулю (по свойству определителя). Таким образом, равенство (5) выполняется, тем самым, доказано, что данные три точки лежат на одной прямой.

Деление отрезка в данном отношении

1. Общий случай.

Если даны две точки и , то координаты третьей точки (см. рис.2), лежащей с ними на одной прямой, равны:

Рис. 2

, (6)

где отношение, в котором точка С делит отрезок АВ.

Утверждение.

Каждой точке прямой АВ соответствует определенное значение параметра t, и, обратно, каждому значению параметра t соответствует единственная точка С на отрезке АВ.

2. Частный случай.

Если точка делит отрезок АВ пополам, то , следовательно, получим формулы:

. (7)

Пример 4. Отрезок АВ, соединяющий точки , разделить в отношении 1:2.

Решение.

По условию требуется найти координаты точки , которая делит отрезок АВ в отношении .

По формуле (6) имеем:

Т.о.,

Выполнить задания:

1. Отрезок АВ соединяет точки и . Найти длину отрезка АВ и угол между ним и положительным направление оси Ох.

2. Найти периметр треугольника, если даны координаты его вершин: .

3. Доказать, что треугольник прямоугольный, если даны координаты его вершин: .

4. Точки и три вершины параллелограмма. Найти четвертую вершину.

5. Отрезок АВ, соединяющий точки и , разделить в отношении .

6. Найти площадь треугольника, вершины которого находятся в точках: .

7. Доказать, что три точки лежат на одной прямой.