Практическое занятие №12

Определенный интеграл, его приложения. Длина дуги кривой. Площадь фигуры

Пусть функция определена на отрезке . Разделим отрезок на n произвольных частей точками , выберем на каждом элементарном отрезке произвольную точку и найдем длину каждого такого отрезка: .

Интегральной суммой для функции на отрезке называется сумма вида , причем эта сумма имеет конечный предел I, если для каждого найдется такое число , что при неравенство выполняется при любом выборе чисел .

Определенным интегралом от функции на отрезке (или в пределах от a до b) называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:

.

Теорема существования определенного интеграла

Если функция непрерывна на , то предел интегральной суммы существует и не зависит от способа разбиения отрезка на элементарные отрезки и от выбора точек . Числа a и b соответственно называются нижним и верхним пределом интегрирования. Если на , то определенный интеграл геометрически представляет собой площадь криволинейной трапеции – фигуры, ограниченной линиями (см. рис.).

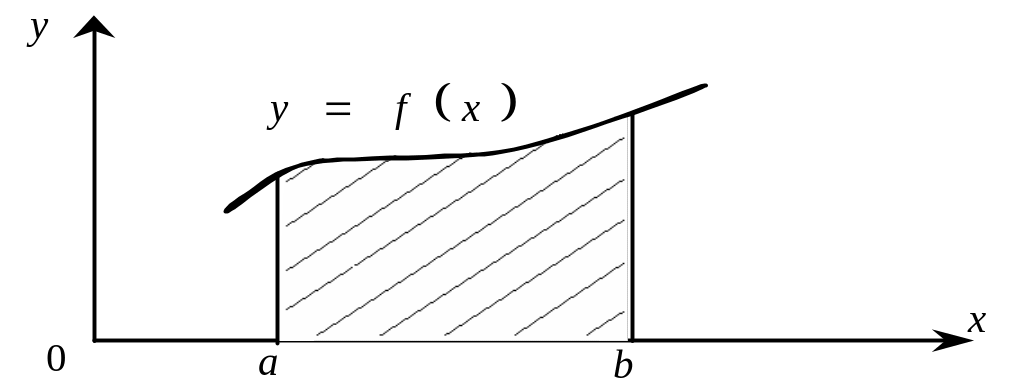
Рис. 5

Основные свойства определенного интеграла

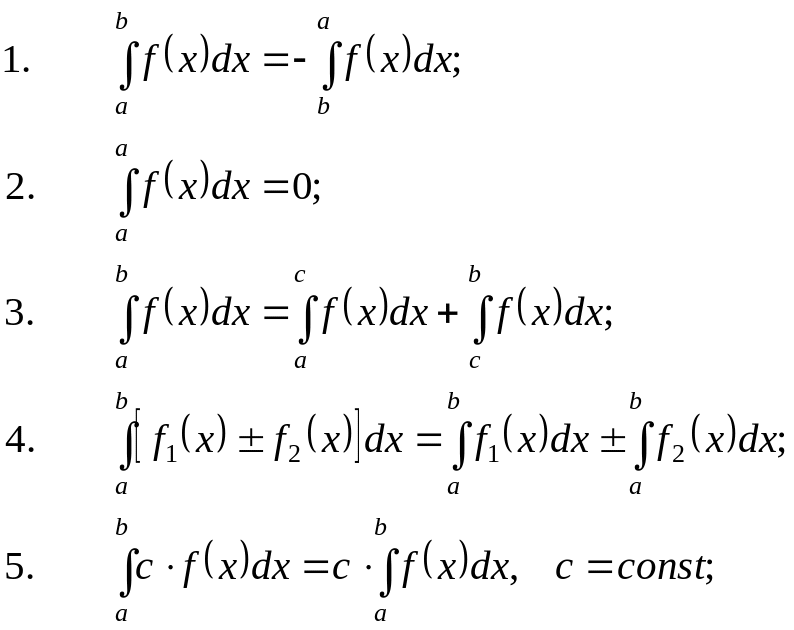
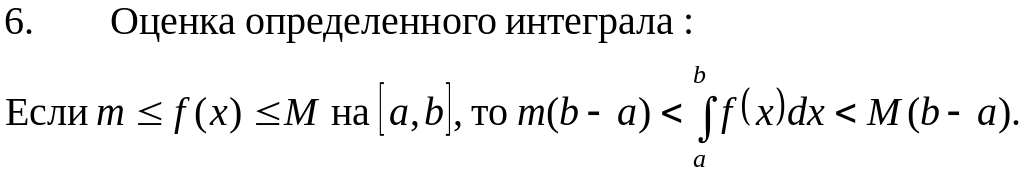
Правила вычисления определенного интеграла

1) Формула Ньютона-Лейбница:

где первообразная для , т.е.

2) Интегрирование по частям:

,

где непрерывно дифференцируемые функции на отрезке .

3) Замена переменной:

где функция, непрерывная вместе со своей производной на отрезке –функция, непрерывная на .

4) Если нечетная функция, т.е. , то

Если четная функция, т.е. то

Пример 1. Найти интегралы:

Решение. a) Применяя таблицу основных интегралов и пользуясь формулой Ньютона-Лейбница получим:

б) Пользуясь свойствами и правилами вычисления определенного интеграла, получаем:

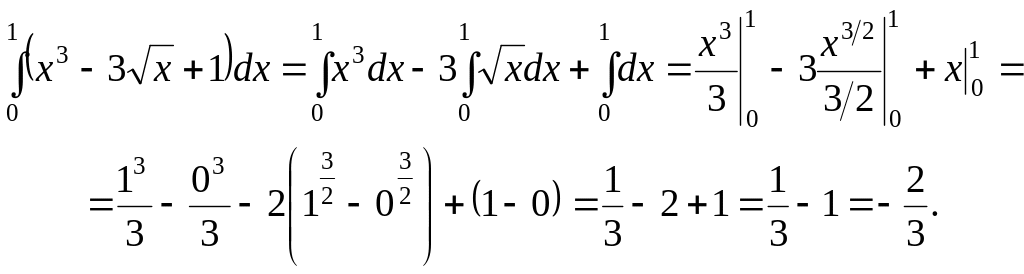
Выполнить задания:

1) Вычислить определенные интегралы:

а) ;

б) ;

в) ;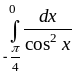

г) ;

д) .

2) Найти длину дуги кривой: .

3) Найти площадь фигуры, ограниченной линией .