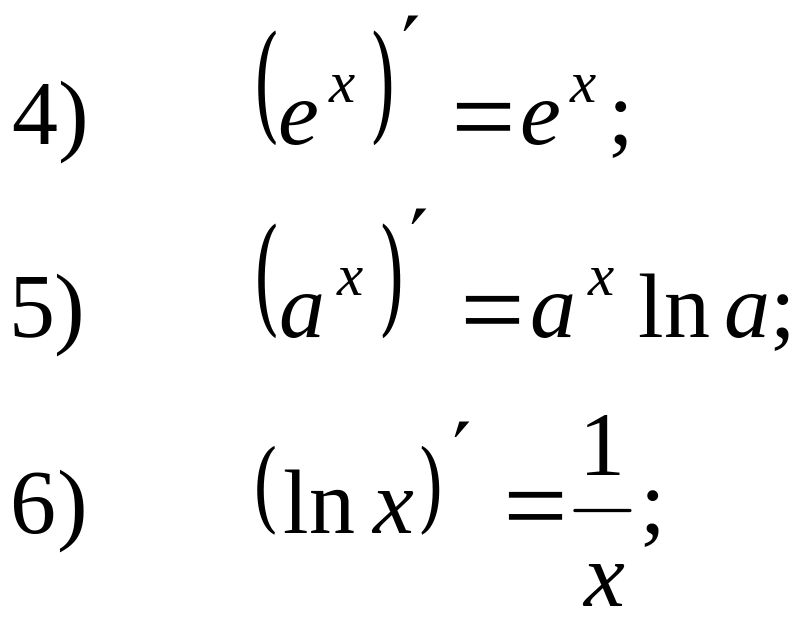Формулы и основные правила дифференцирования функций
|
|
|
|
Основные правила дифференцирования
Пусть
С –
постоянная,
функции,
имеющие производные.
Тогда:
7) если
т.е.
где функции
и
имеют производные, то
(правило дифференцирования сложной
функции).
Пример 3. Применяя формулы и правила дифференцирования, найти производные следующих функций:
Решение. 
.
Применим
правило дифференцирования
:
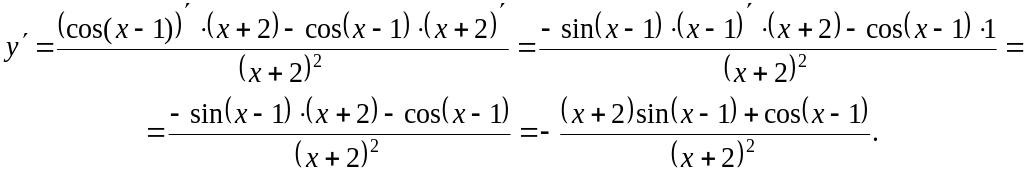
Выполнить задания:
Найти:
а)
если
;
б)
,
если
.
Найти производные функций:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
ж)
|
|
Найти дифференциал dy и приращение
функции
при
.Найти дифференциалы первого порядка функций:
а) 
б) 
в) 
Написать уравнение касательной и нормали к графику функции
в данной точке, если:
а) 
б) 
6) Написать
уравнение касательной к кривой
в точке
.
Практическое занятие №10
Неопределенный интеграл. Непосредственное интегрирование и с использованием таблицы интегралов
Если
для всех
выполняется
,
то функция
называется первообразной
для функции
на множестве
.
Пример
1. 
.
Любая непрерывная функция имеет бесконечное множество первообразных, которые отличаются друг от друга постоянным слагаемым.
Неопределенным
интегралом
от функции
(обозначается
)
называется совокупность всех ее
первообразных:
.
Пример
2.
.
Здесь
знак
интеграла, х
– подынтегральная функция, x
dx –
подынтегральное выражение, х
– интегральная переменная.
Отыскание неопределенного интеграла называется интегрированием функции.
Основные свойства неопределенного интеграла
Таблица основных неопределенных интегралов
|
|
Во
всех формулах 1-18
функция,
имеющая непрерывную производную.
Пример 3. Найти интегралы:
Решение. а) Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов:
1)
,
где
монотонная,
непрерывно дифференцируемая функция
новой переменной t.
Формула замены переменной в этом случае
имеет вид:
2)
Пусть аргументом подынтегральной
функции является функция
,
тогда обозначим
,
где u
– новая переменная. Формула замены
переменной при такой подстановке:
При
нахождении
применим подстановку второго вида.
Пусть
тогда
Имеем:
б) Непосредственным интегрированием получаем:
Выполнить задания:
Применяя табличные интегралы, найти:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Практическое занятие №11 Метод интегрирования заменой переменной и по частям
Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов:
1)
, где
монотонная,
непрерывно дифференцируемая функция
новой переменной t.
Формула замены переменной в этом случае
имеет вид:
2)
Пусть аргументом подынтегральной
функции является функция
,
тогда обозначим
,
где
новая
переменная.
Формула замены переменной при такой подстановке:
Пример
1. Найти
.
Решение.
Пусть
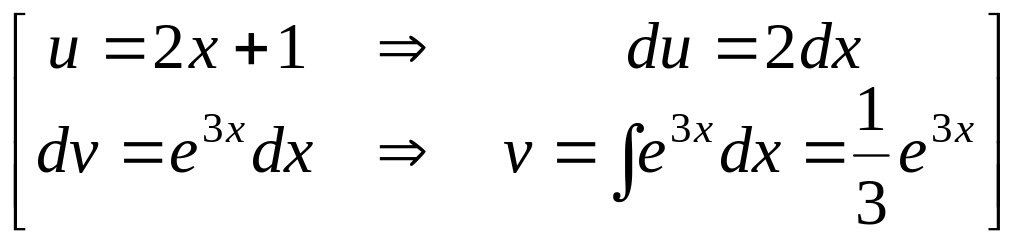(можно положить
).
Следовательно, по формуле интегрирования
по частям:
.
Пример 2. Найти интегралы методом замены переменной:
Решение.
а)
Пусть
,
тогда
Имеем:
Если
дифференцируемые
функции, то справедлива формула:
(1)
Эта формула используется в тех случаях,
когда подынтегральное выражение
можно так представить в виде
так, что стоящий в правой части равенства
(1) интеграл при надлежащем выборе
выражений u и dv может оказаться
проще исходного интеграла.
При этом следует иметь в виду, что к u следует относить множители, которые упрощаются при дифференцировании. Формула (1) может применяться неоднократно.
Укажем некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям.
1. Интегралы вида
где
многочлен,
k – число. Удобно
положить
,
а за
обозначить
все остальные сомножители.
2. Интегралы вида
Удобно положить
,
а за u обозначить
остальные сомножители.
3. Интегралы вида
,
где а и b – числа.
За u
можно принять функцию
.
Пример
3. Найти
.
Решение.
Пусть
.
Поэтому
Пример
4. Найти
Решение.
Пусть
.
Поэтому
Выполнить задания:
1) Вычислить интегралы с помощью замены переменной:
а) 
; б) 
;
в) 
; г) 
;
д) 
; e) 
;
ж) 
; з) 
;
и) 
.
2) Вычислить интегралы, применяя формулу интегрирования по частям:
а) 
;
б) 
;
в) 
.