49

Раздел III. Введение в математический анализ Практическое занятие №9 Предел. Производная явно заданной и сложной функций

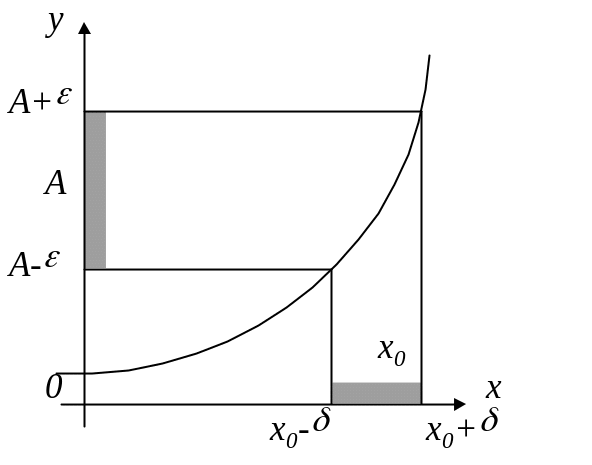
Число А называется пределом функции если функция определена в некоторой окрестности точки , исключая, может быть, саму эту точку, и каково бы ни было число , всегда можно указать такое число , что из выполнения неравенства следует выполнимость неравенства .

Рис.4

Если число А является пределом функции при , пишут . В практике вычисления пределов большое место занимают так называемые первый и второй замечательные пределы: Первый замечательный предел: (х – радианная мера угла).

Второй замечательный предел: , где 2,7182... – иррациональное число, служащее основанием натуральных логарифмов, обозначаемых

Предел – важнейшее понятие математики. Понятие предела опирается на интуитивное представление о процессе изменения и неограниченного приближения.

lim – это первые три буквы латинского слова limes, которое и означает «пределы». Слово limes для обозначения предела впервые употребил И. Ньютон, символ lim ввел французский ученый С. Люилье в 1786г., а выражение первым записал У. Гамильтон в 1855г.

Пример 1. а) Найти предел .

Решение. Используя теоремы о пределах, находим

.

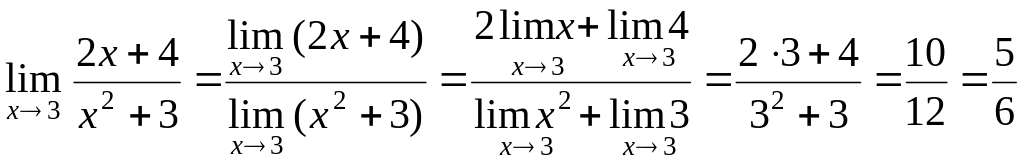б) Найти предел .

Решение. Если предел знаменателя равен нулю, а предел числителя не равен нулю, то предел дроби равен бесконечности:

,

где означает, что х принимает значения больше 3.

Если имеем неопределенность вида или , необходимы преобразования.

в) Найти предел: .

Числитель и знаменатель дроби при равны нулю. Выполним тождественные преобразования: решим квадратные уравнения

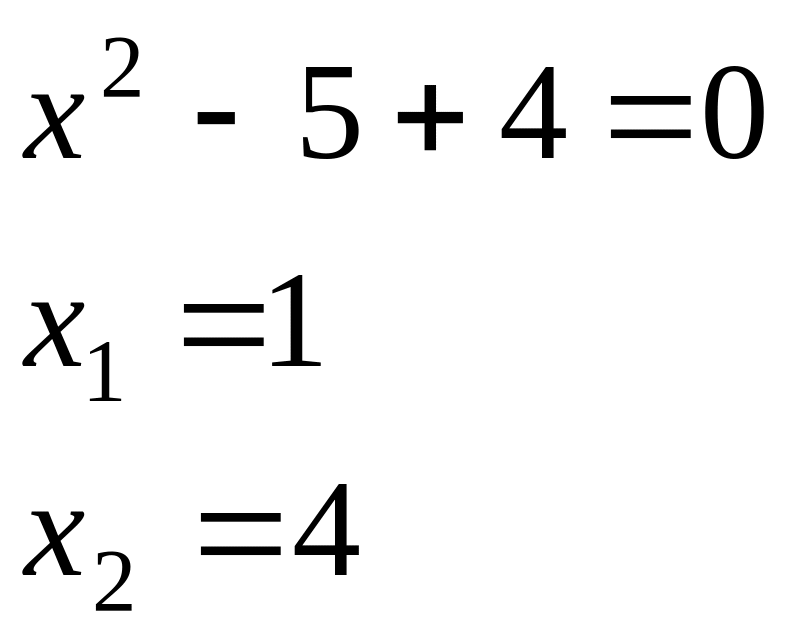и

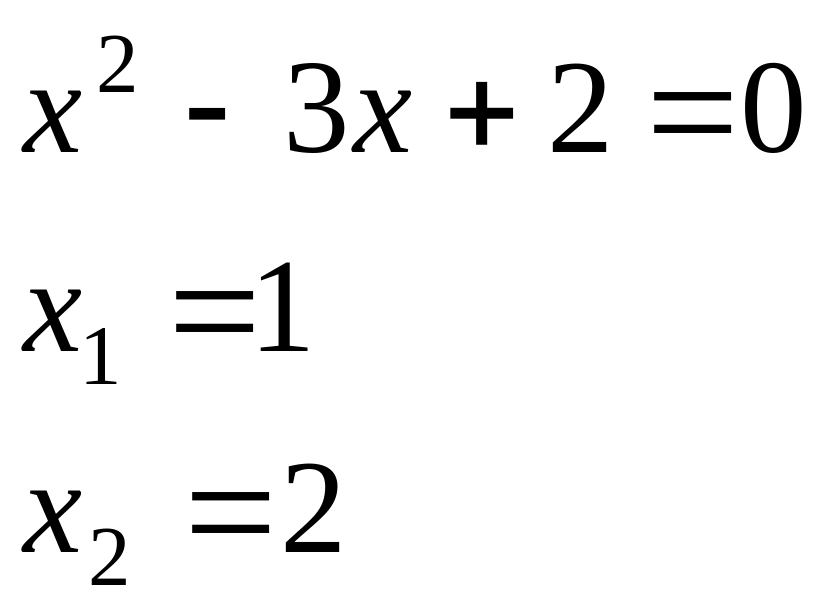
Квадратный трехчлен , где числа, не равные нулю, х – переменная, можно разложить на множители по формуле:

где корни квадратного трехчлена.

Т.о.

Функции совпадают в окрестности точки , поэтому их пределы равны при :

.

г) Найти предел: .

Преобразуем дробь, разделив числитель и знаменатель на :

.

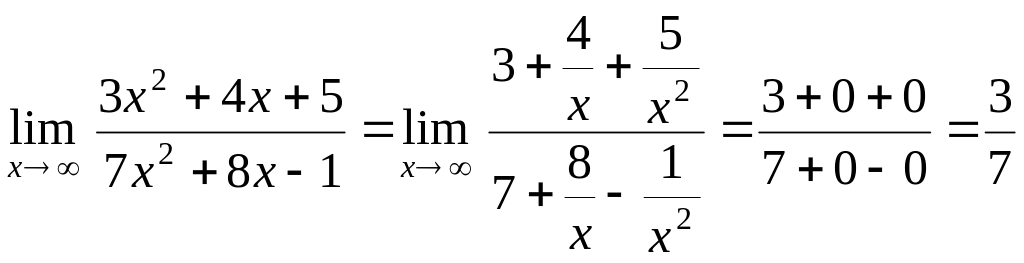Совокупность всех значений переменной, которые она может принять в условиях рассматриваемого вопроса, называется областью изменения этой переменной. Основным вопросом математического анализа является не изучение изменения одной переменной самой по себе, а изучение зависимости между двумя или несколькими переменными при их совместном изменении.

Если между двумя переменными имеется такая связь, что значения, одной из них определяются значениями другой, то говорят, что эти переменные связаны между собой функциональной зависимостью.

Если в силу некоторого правила каждому значению переменной х из ее области изменения соответствует одно определенное значение переменной у, то переменная у называется функцией переменной х.

Область изменения аргумента х называют областью определения функции у.

Пример 2. а) Областью определения функции служит отрезок , т.е. совокупность значений х, удовлетворяющих соотношениям .

б) Областью определения функции является отрезок , т.к.

Пусть и значения аргумента, а соответствующие значения функции Разность называется приращением аргумента, а разность приращением функции на отрезке .

Производной от функции по аргументу х называется конечный предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:

.

Производная обозначается также . Геометрически производная представляет собой угловой коэффициент касательной к графику функции в точке х, т.е. .

Производная есть скорость изменения функции в точке х.

Отыскание производной называется дифференцированием функции.