4.4 Параметри функціонування замкнутої Пуассонівської системи масового обслуговування при кількості постів обслуговування більше 1

Якщо n>5, то усі параметри функціонування замкнутої Пуассонівської системи масового обслуговування визначають для n=1,2,3,4,5 і n, яке дорівнює розрахованому числу постів обслуговування (в нашому випадку n=3).

Оскільки n>1, то доцільно для розрахунку ймовірностей використовувати рекурентні формули [1]:

, (4.16)

де (4.17)

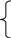, 0<kn,

Y_k= (4.18)

, n<km.

. (4.19)

Скориставшись формулами (4.19), (4.17) та (4.18) визначимо характеристики системи масового обслуговування при n=3, m=13, ^’=0,005 хв^-1, =0,014 хв^-1.

=^’/=0,005/0,014=0,357.

₀=1; ;

; ;

; ;

……. .

Розрахунок ведемо до k=m, або коли точність розрахунку визначається чотирма нулями після коми (у нашому прикладі розрахунок виконуємо до k=m=13).

Визначаємо суму =4,998+11,598+…+0,3765=187,822.

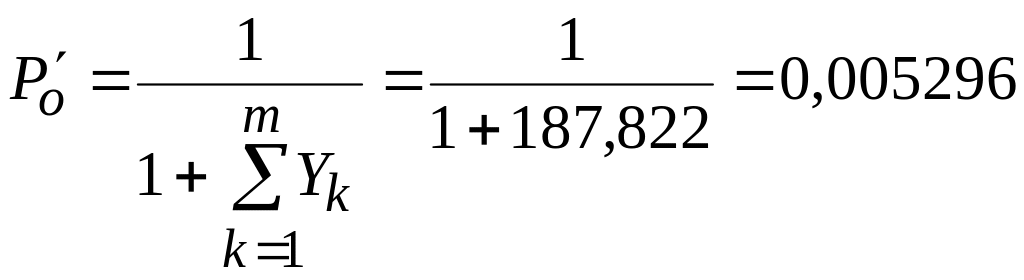
(4.20)

Після визначення Р₀ за формулою (4.16) розрахуємо:

Р₁=Y₁ Р₀=4,9980,005296=0,02647;

Р₂=Y₂ Р₀=11,5980,005296=0,06142 і т.д.

Результати розрахунків заносимо у таблицю 4.1.

Середнє число автомобілів, які очікують навантаження в цьому випадку визначатиметься за формулою [1]:

=Р₄+2Р₅+…+10Р₁₃=0,114813251+20,136627769+…

…+100,001993782=3,09 (4.21)

Середня кількість навантажувальних механізмів, що простоюють внаслідок відсутності автомобілів визначається за формулою [1]:

=3Р₀+2Р₁+Р₂=30,00529598+20,026469308+

+0,061422029=0,114. (4.22)

Середній час простою автомобіля в пункті навантаження, хв.. визначається за формулою [1]:

, (4.23)

де:

,

.

Таблиця 4.1 – Результати розрахунків Пуассонівської системи масового обслуговування при n>1

k	Yk	Pk	kPk	(k-n)Pk	(n-k)Pk
1	2	3	4	5	6
0 1 2 3 4 5 6 7 8 9 10 11 12 13	1 4,998 11,597859 16,56174265 21,67932113 25,79829215 27,63007799 26,30383425 21,91109393 15,64452106 9,308490033 4,430841256 1,581810328 0,376470858	0,00529598 0,026469308 0,061422029 0,87710658 0,11481325 0,136627769 0,14632834 0,13930458 0,116040715 0,082853071 0,049297577 0,023465647 0,008377236 0,001993782	0 0,026469308 0,122844059 0,263131974 0,459253005 0,683138844 0,877970043 0,975162061 0,928325722 0,745677636 0,49297577 0,258122113 0,10052683 0,025919168	0 0 0 0 0,114813251 0,273255538 0,438985021 0,55721832 0,580203576 0,497118424 0,345083039 0,187725173 0,075395123 0,019937821	0,015887941 0,052938616 0,61422029 0
	187,8224546	0,994703963	5,96	3,09	0,114

Середній час очікування навантаження, хв. визначається за формулою [1]:

=125-69,18=55,82 хв. (4.24)

За результатами розрахунків зробити висновки.