2. Модели авторегрессии
Достаточно распространены авторегрессионные модели вида:
.
(8.1)
Для модели (8.1), как
и в модели с распределенными лагами,
параметр
характеризует краткосрочное изменение
под воздействием
на 1 единицу. Параметр
по существу представляет собой величину
из преобразования Койка, т.е.
и показывает коэффициент снижения
лаговых коэффициентов при увеличении
значения лага в соответствии с концепцией
их геометрического убывания. Следовательно,
к моменту времени
результат
изменится дополнительно на
единиц, а к моменту времени
дополнительное изменение
составит
единиц, к моменту времени
-
и т.д. Соответственно долгосрочный
мультипликатор окажется равным:
(в предположении
бесконечного числа лагов).
Учитывая геометрическую прогрессию лаговых коэффициентов,
- долгосрочный
мультипликатор изменения
.
В силу того, что в авторегрессии в правой части содержатся лаговые эндогенные переменные, принято считать, что оценка параметров традиционным МНК дает неудовлетворительные результаты.
Предположим, что рассматривается модель авторегрессии вида (8.1) .
Применение для
оценивания параметров уравнения (8.1)
традиционного МНК возможно, если
выполняется предпосылка МНК относительно
отсутствия автокорреляции остатков.
Между тем при наличии в правой части
лаговой зависимой переменной может
иметь место автокорреляция остатков.
Кроме того, может иметь место и зависимость
объясняющей переменной
с остатками
,
т.е. нарушается предпосылка о
гомоскедастичности остатков. В силу
этого классический метод наименьших
квадратов в малых выборок даст смещенные
оценки параметров.
Одним из возможных методов оценивания параметров модели (8.1) является метод инструментальных переменных. Суть метода состоит в том, что вместо лаговой зависимой переменной , для которой нарушается предпосылка МНК, используется другая переменная, называемая инструментальной. При этом инструментальная переменная должна обладать двумя свойствами:
она должна быть тесно коррелированна с лаговой переменной ;
она не должна коррелировать с остатками
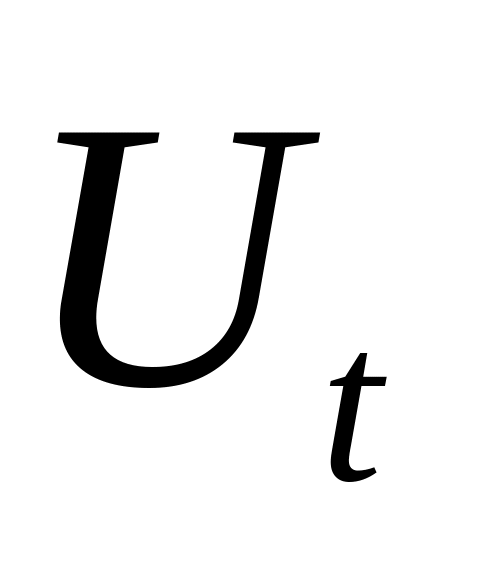(случайными ошибками).
Иными словами, от модели авторегрессии (8.1) необходимо перейти к модели вида:
.
(8.2)
Результаты регрессии
по модели (8.2), естественно, зависят от
того, насколько удачно подобрана
инструментальная переменная. В качестве
инструментальной переменной можно,
например, взять оценку
,
т.е.
,
полученную по регрессии
от
.
Поскольку в модели (8.1) предполагается наличие зависимости от , то можно предположить, что также имеет место зависимость от , т.е. найдем регрессию
.
. (8.3)
Используя для
оценки параметров уравнения (8.3) обычный
МНК, что возможно ввиду отсутствия в
правой части модели лаговой зависимой
переменной, найдем теоретические
значения
,
которые и будут рассматриваться как
значения инструментальной переменной
в модели (8.2). Далее вновь применяем МНК
уже к модели (8.2), т.е. по существу оценка
параметров модели авторегрессии (8.1)
будет найдена исходя из модели вида
.
(8.4)
Если вместо оценки подставить выражение (8.3), то получим следующую модель:
.
(8.5)
Она представляет собой модель с распределенным лагом, оценка параметров которой может быть дана МНК.
Таким образом, используя в качестве инструментальной переменной оценки , исходя из регрессии (8.3), модель авторегрессии (8.1) заменяется на модель с распределенным лагом (8.5).