3. Устранение гетероскедастичности

При установлении гетероскедастичности возникает необходимость преобразования модели с целью устранения данного недостатка. Вид преобразования зависит от того, известны или нет дисперсии отклонений .

Метод взвешенных наименьших квадратов (ВНК) применяется для известных для каждого наблюдения значениях . В этом случае можно устранить гетероскедастичность, разделив каждое наблюдаемое значение на соответствующее ему значение среднего квадратического отклонения. В этом суть метода взвешенных наименьших квадратов.

Для простоты изложения опишем ВНК на примере парной регрессии:

. (5.8)

Разделим обе части (5.8) на известное :

. (5.9)

Положив , получим уравнение регрессии без свободного члена, но с дополнительной объясняющей переменной Z и с «преобразованным» отклонением :

. (5.10)

При этом для выполняется условие гомоскедастичности. Действительно, . Так как по предпосылке 1⁰ МНК , то , и тогда

.

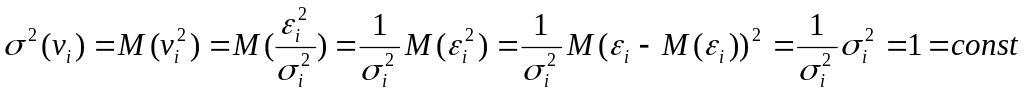Следовательно, для преобразованной модели (5.10) выполняются предпосылки 1⁰-5⁰ МНК. В этом случае оценки, полученные по МНК, будут наилучшими линейными несмещенными оценками.

Для применения ВНК необходимо знать фактические значения дисперсий отклонений. На практике такие значения известны крайне редко. следовательно, чтобы применить ВНК, необходимо сделать реалистические предположения о значениях .

Например, может оказаться целесообразным предположить, что дисперссии отклонений пропорциональны значениям (рис. 5.4,а) или значениям (рис. 5.4,б).

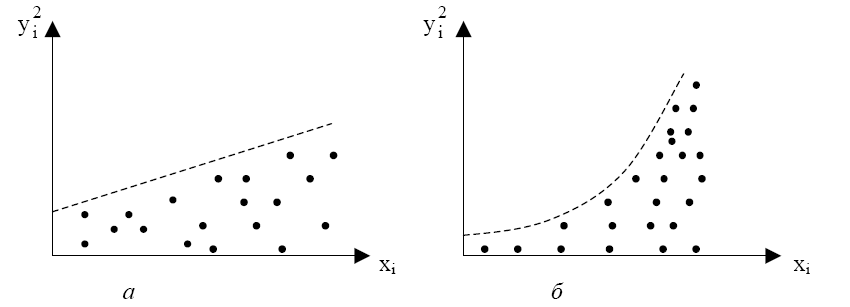
Рис. 5. 4

Дисперсии пропорциональны (рис 5.4,а):

( - коэффициент пропорциональности).

Тогда уравнение (5.8) преобразуется делением его левой и правой частей на :

. (5.11)

Несложно показать, что для случайных отклонений выполняется условие гомоскедастичности. Следовательно, в регрессии (5.11) применим обычный МНК. Действительно, в силу выполнимости предпосылки имеем:

.

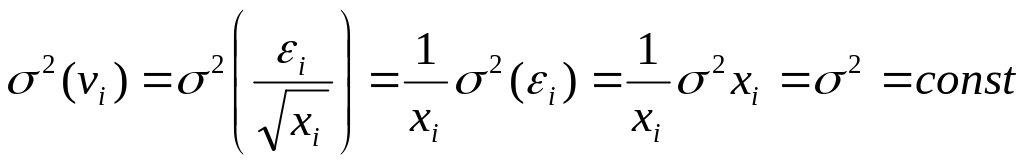Таким образом, оценив для (5.11) по МНК коэффициенты и , затем возвращаются к исходному уравнению регрессии (5.8).

4. Автокорреляция остатков, ее последствия. Обнаружение автокорреляции остатков

Автокорреляция остатков обычно встречается в регрессионном анализе при использовании данных временных рядов. Поэтому в дальнейших выкладках вместо символа i используется символ t, отражающий момент наблюдения, объем выборки при этом будем обозначать символом T. В экономических задачах значительно чаще встречается так называемая положительная автокорреляция ( ), нежели отрицательная автокорреляция ( ).

В большинстве случаев положительная автокорреляция вызывается направленным постоянным воздействием некоторых неучтенных в модели факторов.

Среди основных причин, вызывающих появление автокорреляции, можно выделить ошибки спецификации, инерцию в изменении экономических показателей, эффект паутины, сглаживание данных.

Последствия автокорреляции в определенной степени сходны с последствиями гетероскедастичности. Среди них при применении МНК обычно выделяют следующие:

1. Оценки параметров, оставаясь линейными и несмещенными, перестают быть эффективными. Следовательно, они перестают обладать свойствами наилучших линейных несмещенных оценок (BLUE-оценок).

2. Дисперсии оценок являются смещенными. Часто дисперсии, вычисляемые по стандартным формулам, являются заниженными, что влечет за собой увеличение -статистик. Это может привести к признанию статистически значимыми объясняющие переменные, которые в действительности таковыми могут и не являться.

3. Оценка дисперсии регрессии 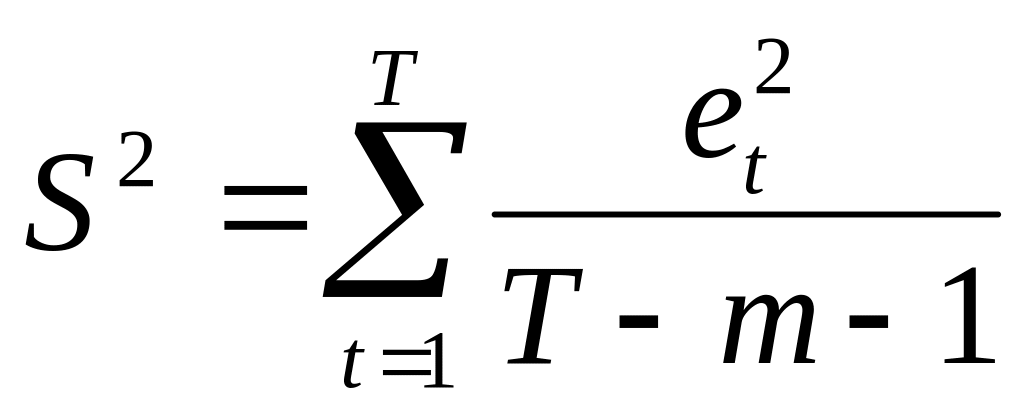является смещенной оценкой истинного значения 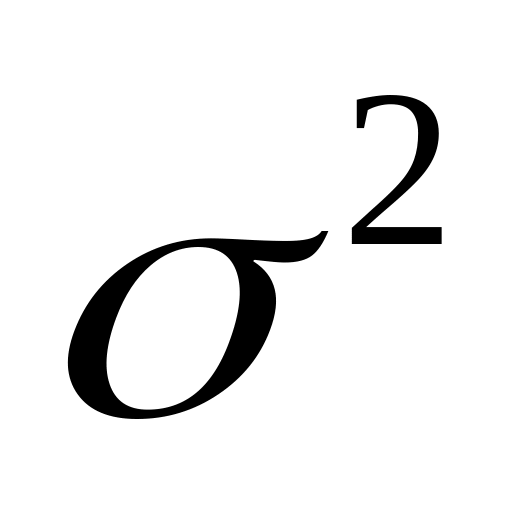, во многих случаях занижая его.

4. В силу вышесказанного выводы по - и -статистикам, определяющим значимость коэффициентов регрессии и коэффициента детерминации, возможно, будут неверными. Вследствие этого ухудшаются прогнозные качества модели.

В силу неизвестности значений параметров уравнения регрессии неизвестными будут также и истинные значения отклонений . Поэтому выводы об их независимости осуществляются на основе оценок , полученных из эмпирического уравнения регрессии. Рассмотрим возможные методы определения автокорреляции.

1. Графический метод.

Существует несколько вариантов графического определения автокорреляции. Один из них, увязывающий отклонения с моментами их получения (их порядковыми номерами ), приведен на рис. 5.5. Это так называемые последовательно-временные графики. В этом случае по оси абсцисс обычно откладываются либо время (момент) получения статистических данных, либо порядковый номер наблюдения, а по оси ординат – отклонения (либо оценки отклонений ).

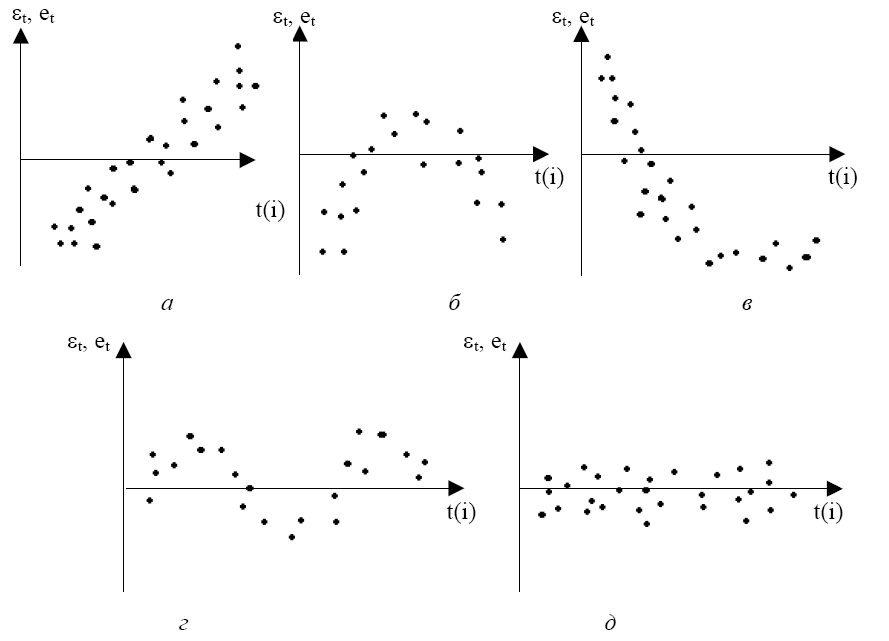
Рис. 5. 5

Естественно предположить, что на рис. 5.5, а-г имеются определенные связи между отклонениями, т.е. автокорреляция имеет место. Отсутствие зависимости на рис. 5.5,д скорее всего свидетельствует об отсутствии автокорреляции.

Например, на рис. 5.5,б отклонения вначале в основном отрицательные, затем положительные, потом снова отрицательные. Это свидетельствует о наличии между отклонениями определенной зависимости. Более того, можно утверждать, что в этом случае имеет место положительная автокорреляция остатков. Она становится весьма наглядной, если график 5.5,б дополнить графиком зависимости от (рис. 5.6).

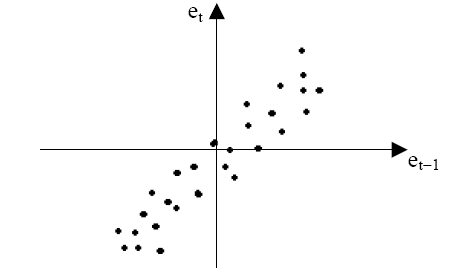
Рис. 5. 6

Подавляющее большинство точек на этом графике расположено в I и III четвертях декартовой системы координат, подтверждая положительную зависимость между соседними отклонениями.

Следует заметить, что в современных компьютерных прикладных программах для решения задач по эконометрике аналитическое выражение регрессии дополняется графическим представлением результатов. На график реальных колебаний зависимой переменной накладывается график колебаний переменной по уравнению регрессии. Сопоставив эти два графика, можно выдвинуть гипотезу о наличии автокорреляции остатков. Если эти графики пересекаются редко, то можно предположить наличие положительной автокорреляции остатков.

2. метод рядов.

Этот метод достаточно прост: последовательно определяются знаки отклонений . Например,

(-----)(+++++++)(---)(++++)(-),

т.е. 5 «-», 7 «+», 3 «-», 4 «+», 1 «-» при 20 наблюдениях.

Ряд определяется как непрерывная последовательность одинаковых знаков. Количество знаков в ряду называется длиной ряда.

Визуальное распределение знаков свидетельствует о неслучайном характере связей между отклонениями. Если рядов слишком мало по сравнению с количеством наблюдений , то вполне вероятна положительная автокорреляция. Если же рядов слишком мало, то вероятна отрицательная автокорреляция. Для более детального анализа предлагается следующая процедура. Пусть

– объем выборки;

– общее количество знаков «+» при наблюдениях (количество положительных отклонений );

– общее количество знаков «-» при наблюдениях (количество положительных отклонений );

– количество рядов.

При достаточно большом количестве наблюдений ( ) и отсутствии автокорреляции СВ имеет асимптотически нормальное распределение с

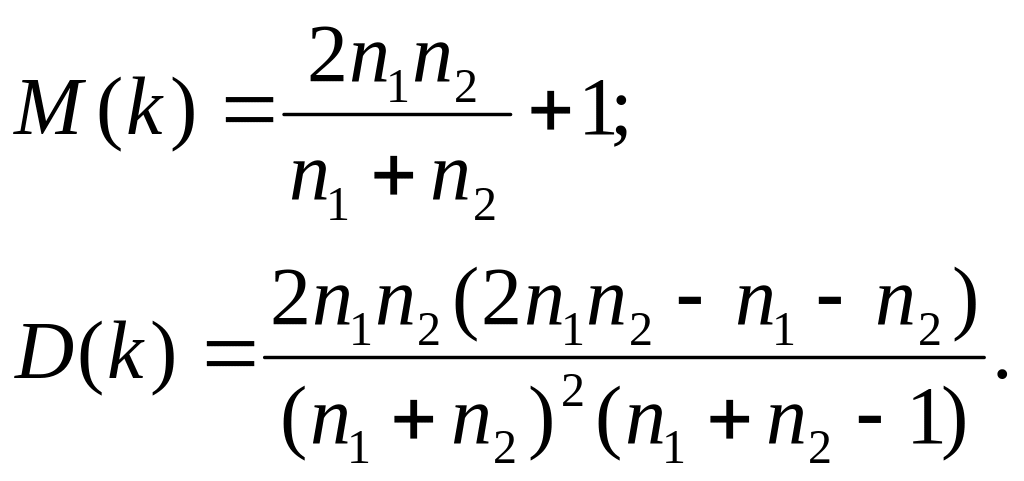
Тогда, если , то гипотеза об отсутствии автокорреляции не отклоняется.

Для небольшого числа наблюдений ( ) Свед и Эйзенхарт разработали таблицы критических значений количества рядов при наблюдениях . Суть таблиц в следующем.

На пересечении строки и столбца определяются нижнее и верхнее значения при уровне значимости .

Если , то говорят об отсутствии автокорреляции.

Если , то говорят о положительной автокорреляции.

Если , то говорят об отрицательной автокорреляции.

В нашем примере . По таблицам определяем . Поскольку , то применяется предположение о наличии положительной автокорреляции при уровне значимости .

3. Критерий Дарбина-Уотсона.

Наиболее известным критерием обнаружения автокорреляции первого порядка является критерий Дарбина-Уотсона. Общая схема критерия Дарбина-Уотсона изложена в моделях временных рядов (см.тема7,стр. ).

При установлении автокорреляции необходимо в первую очередь

проанализировать правильность спецификации модели.Если после ряда

усовершенсвований регрессии автокорреляция по-прежнему имеет место, то возможны определенные преобразования, устраняющие автокорреляцию. Среди них выделяется авторегрессионная схема первого порядка AR(1).