
- •Эконометрического моделирования План лекции
- •Введение
- •1.Предмет, цель и задачи эконометрики.
- •2.Этапы становления эконометрики
- •3. Введение в эконометрическое моделирование
- •4. Основные математические предпосылки эконометрического моделирования
- •5. Основные этапы и проблемы эконометрического моделирования
- •Контрольные вопросы:
- •Тема 2. Парная линейная регрессия и корреляция План лекции
- •Введение
- •1. Модель линейной парной регрессии. Метод наименьших квадратов
- •2. Коэффициент корреляции
- •3. Основные положения регрессионного анализа. Теорема Гаусса – Маркова
- •4. Оценка значимости уравнения регрессии. Коэффициент детерминации
- •5. Построение интервальных прогнозов по модели парной регрессии
- •Контрольные вопросы:
- •Тема 3. Множественный регрессионный анализ План лекции
- •Введение
- •1. Классическая нормальная линейная модель множественной регрессии
- •2. Оценка параметров классической регрессионной модели методом наименьших квадратов
- •3. Предпосылки для множественного регрессионного анализа.
- •Теорема Гаусса-Маркова.
- •4. Стандартизированное уравнение линейной множественной регрессии
- •Контрольные вопросы:
- •Тема 4. Множественная корреляция План лекции
- •Введение
- •1. Множественная линейная корреляционная зависимость
- •2. Частные коэффициенты корреляции
- •3. Коэффициент множественной корреляции
- •4. Отбор факторов в случае линейной множественной регрессии
- •Контрольные вопросы:
- •Тема 5. Линейные регрессионные модели
- •1. Суть гетероскедастичности, ее последствия
- •2. Тесты, позволяющие выявить наличие гетероскедастичности остатков
- •3. Устранение гетероскедастичности
- •4. Автокорреляция остатков, ее последствия. Обнаружение автокорреляции остатков
- •Контрольные вопросы:
- •Тема 6. Линейные регрессионные модели
- •1. Фиктивные переменные
- •2. Модели регрессии с фиктивными переменными сдвига
- •3. Модели регрессии с фиктивными переменными наклона
- •4. Критерий г. Чоу
- •Контрольные вопросы:
- •Тема 7. Модели временных рядов План лекции
- •Введение
- •1. Понятие временного ряда. Общий вид модели временного ряда
- •2. Проверка гипотезы существования тенденции
- •3. Стационарные временные ряды и их характеристики. Автокорреляционная функция
- •Авторегрессия первого порядка. Тест Дарбина-Уотсона
- •4. Аналитическое выравнивание (сглаживание) временного ряда
- •6. Процесс построения аддитивной модели временного ряда
- •7. Прогнозирование на основе моделей временного ряда
- •8. Понятие об авторегрессионных моделях и моделях скользящей средней
- •Контрольные вопросы:
- •Тема 8: модели с лаговыми переменными План лекции
- •Введение
- •1. Модели с распределенными лагами
- •2. Модели авторегрессии
- •3. Авторегрессионные модели и их моделирование
- •Контрольные вопросы:
- •Тема 9. Системы линейных одновременных уравнений План лекции
- •Введение
- •1. Структурная и приведенная формы моделей
- •2. Проблема идентификации
- •Матрица коэффициентов (1)
- •Матрица коэффициентов (2)
- •Матрица коэффициентов (3)
- •3. Оценивание параметров структурной модели
- •Условные данные по пяти регионам
- •Контрольные вопросы:
- •Используемая литература
3. Стационарные временные ряды и их характеристики. Автокорреляционная функция
Важное значение в анализе временных рядов имеют стационарные временные ряды, вероятностные свойства которых не изменяются во времени.
Временной ряд
называется стационарным,
если совместное распределение вероятностей
наблюдений
![]() такое же, как и
наблюдений
такое же, как и
наблюдений
![]() при любых
,
при любых
,
![]() и
и
![]() .
Другими словами, свойства строго
стационарных рядов
.
Другими словами, свойства строго
стационарных рядов
![]() не зависят от момента
,
т.е. закон распределения и его числовые
характеристики не зависят от
.
Следовательно, математическое ожидание
не зависят от момента
,
т.е. закон распределения и его числовые
характеристики не зависят от
.
Следовательно, математическое ожидание
![]() ,
среднее квадратическое отклонение
,
среднее квадратическое отклонение
![]() могут
быть оценены по наблюдениям с помощью
формул:
могут
быть оценены по наблюдениям с помощью
формул:
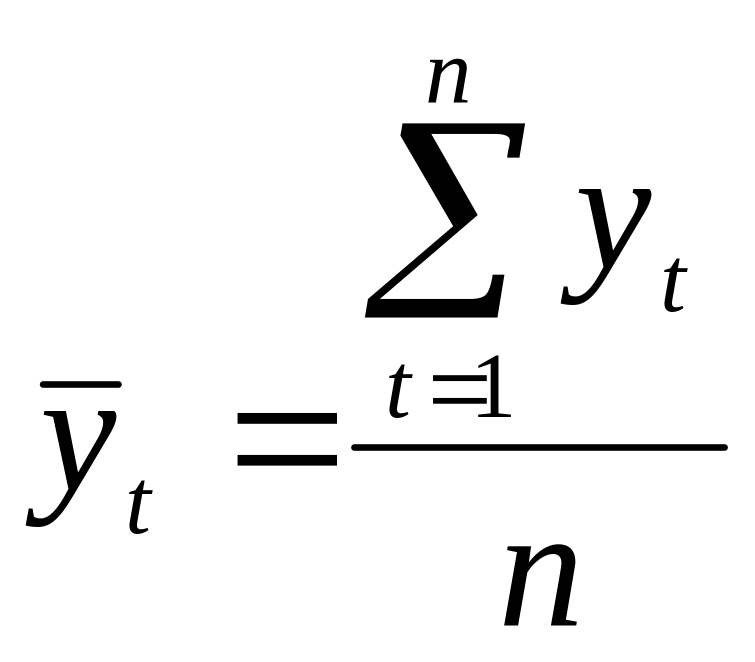 (7.4)
(7.4)
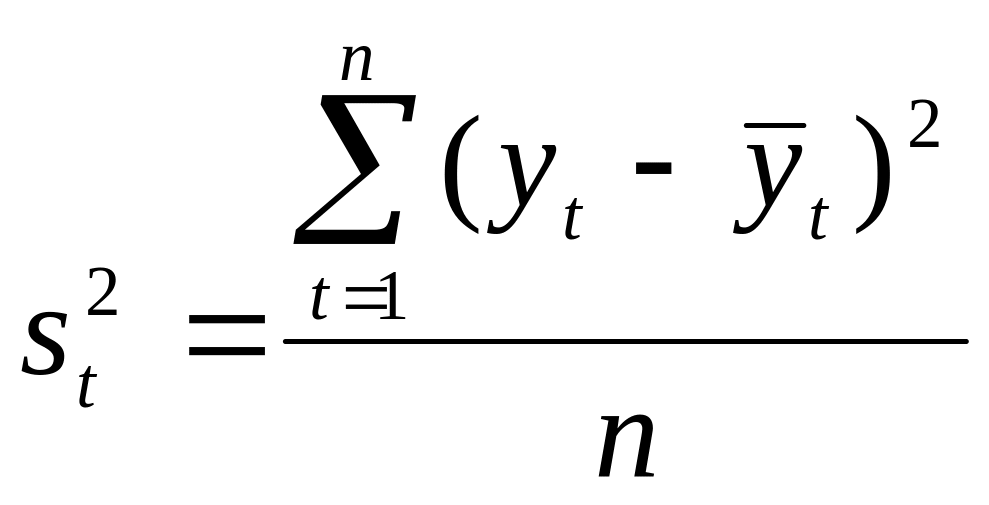 (7.5)
(7.5)
Простейшим примером стационарного временного ряда, у которого математическое ожидание равно нулю, а ошибки некоррелированы, является «белый шум».
Степень тесноты связи между последовательностями наблюдений временного ряда и (сдвинутых относительно друг друга на единиц, или, как говорят, с лагом ) может быть определена с помощью коэффициента корреляции
![]() (7.6)
(7.6)
Т.к.
![]() измеряет корреляцию между членами
одного и того же ряда, его называют
коэффициентом
автокорреляции,
а зависимость
– автокорреляционной
функцией.
В силу стационарности временного ряда
автокорреляционная функция
зависит только от лага
,
причем
измеряет корреляцию между членами
одного и того же ряда, его называют
коэффициентом
автокорреляции,
а зависимость
– автокорреляционной
функцией.
В силу стационарности временного ряда
автокорреляционная функция
зависит только от лага
,
причем
![]() ,
т.е. при изучении можно ограничиться
рассмотрением только положительных
значений
.
,
т.е. при изучении можно ограничиться
рассмотрением только положительных
значений
.
Статистической
оценкой
является выборочный
коэффициент автокорреляции
![]() ,
определяемый по формуле:
,
определяемый по формуле:
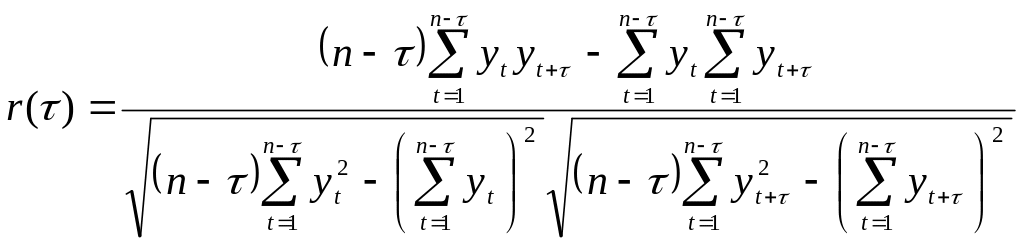 (7.7)
(7.7)
Функцию называют выборочной автокорреляционной функцией, а ее график – коррелограммой.
При расчете
следует
помнить, что с увеличением
число
![]() пар наблюдений
пар наблюдений
![]() уменьшается, поэтому лаг
должен быть таким, чтобы число
было достаточным для определения
.
Обычно ориентируются на соотношение
уменьшается, поэтому лаг
должен быть таким, чтобы число
было достаточным для определения
.
Обычно ориентируются на соотношение
![]() .
.
Для стационарного временного ряда с увеличением лага взаимосвязь членов временного ряда ослабевает, и автокорреляционная функция должна убывать (по абсолютной величине). В то же время для ее выборочного (эмпирического) аналога , особенно при небольшом числе пар наблюдений , свойство монотонного убывания (по абсолютной величине) при возрастании может нарушаться.
Наряду с
автокорреляционной функцией при
исследовании стационарных рядов
рассматривается частная
автокорреляционная функция
![]() ,
где
есть частный
коэффициент корреляции между членами
временного ряда
, т.е. коэффициент корреляции между
и при устранении влияния промежуточных
между
и
членов.
,
где
есть частный
коэффициент корреляции между членами
временного ряда
, т.е. коэффициент корреляции между
и при устранении влияния промежуточных
между
и
членов.
Статистической
оценкой
является выборочная
частная автокорреляционная функция
![]() ,
где
– выборочный
частный коэффициент корреляции,
определяемый по формуле (7.6) или (7.7).
Например, выборочный частный коэффициент
автокорреляции 1-го порядка между членами
временного ряда
,
где
– выборочный
частный коэффициент корреляции,
определяемый по формуле (7.6) или (7.7).
Например, выборочный частный коэффициент
автокорреляции 1-го порядка между членами
временного ряда
![]() при устранении влияния
при устранении влияния
![]() может быть вычислен по формуле:
может быть вычислен по формуле:
![]() (7.8)
(7.8)
где
![]() – выборочные коэффициенты автокорреляции
между
и
– выборочные коэффициенты автокорреляции
между
и
![]() и
и
![]() и
и
![]() .
.
Пример 2
Таблица 2
Год, |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Спрос, |
213 |
171 |
291 |
309 |
317 |
362 |
351 |
361 |
Приведены данные, отражающие спрос на некоторый товар за восьмилетний период (усл. ед.), т.е. временной ряд спроса .
По данным таблицы
2 для временного ряда найти среднее
значение, среднее квадратическое
отклонение, коэффициенты автокорреляции
(для лагов
![]() )
и частный коэффициент автокорреляции
1-го порядка.
)
и частный коэффициент автокорреляции
1-го порядка.
Решение.
Среднее значение временного ряда находим по формуле:
![]() (ед.).
(ед.).
Дисперсию и среднее квадратическое отклонение можно вычислить по формуле, но в данном случае проще использовать соотношение
![]()
![]() (ед.)
(ед.)
где
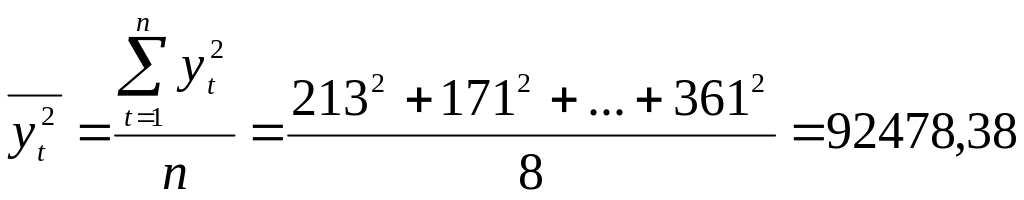
Найдем коэффициент
автокорреляции
временного ряда (для лага
![]() ),
т.е. коэффициент корреляции между
последовательностями семи пар наблюдений
и
),
т.е. коэффициент корреляции между
последовательностями семи пар наблюдений
и
![]() :
:
|
213 |
171 |
291 |
309 |
317 |
362 |
351 |
|
171 |
291 |
309 |
317 |
362 |
351 |
361 |
Вычисляем необходимые суммы:
![]()
![]()
![]()
![]()
![]()
Теперь по формуле (7.7) коэффициент автокорреляции
![]() .
.
Коэффициент
автокорреляции
![]() для лага
для лага
![]() между членами ряда
между членами ряда
![]() по шести парам наблюдений вычисляем
аналогично:
по шести парам наблюдений вычисляем
аналогично:
![]() .
.
Для определения
частного коэффициента корреляции 1-го
порядка
![]() между членами ряда
между членами ряда
![]() при исключении влияния
при исключении влияния
![]() вначале найдем (по аналогии с предыдущим)
коэффициент автокорреляции
вначале найдем (по аналогии с предыдущим)
коэффициент автокорреляции
![]() между
членами ряда:
и
между
членами ряда:
и
![]() :
:![]() ,
а затем вычислим
,
а затем вычислим
![]() по
формуле (7.8):
по
формуле (7.8):
![]()
Знание автокорреляционных функций оказывает существенную помощь при подборе и идентификации модели анализируемого временного ряда и статистической оценке его параметров.
