2. Частные коэффициенты корреляции

Обычно кроме анализа таблицы парных коэффициентов корреляции для отбора существенных факторов вычисляют частные коэффициенты корреляции, определяют надежность полученных коэффициентов регрессии по t – критерию и другие методы.

При анализе последней таблицы парных коэффициентов корреляции связи можно обратить внимание на то, что связи между изучаемыми переменными довольно сложным образом переплетаются между собой. Поэтому целесообразно рассмотреть вопрос о взаимосвязи между факторами при условии, что некоторые или все остальные факторы остаются неизменными.

Для выявления такой взаимосвязи используются коэффициенты частной корреляции.

Вычислим коэффициент частной корреляции между факторами у и х₁ при условии, что фактор х₂ закреплен на постоянном уровне (остается неизменным), тогда он равен

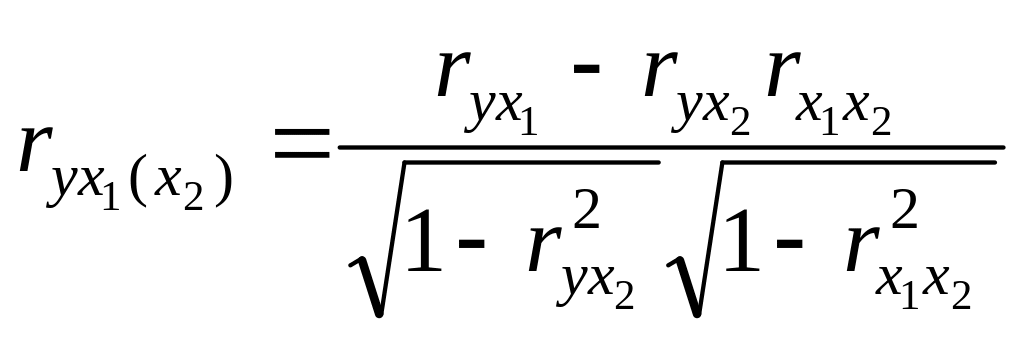(4.2)

Если закреплен лишь один фактор, то такой коэффициент корреляции называется частным коэффициентом корреляции первого порядка. Если закреплены два фактора, то – второго порядка и т.д. Тогда обычный коэффициент парной корреляции можно называть частным коэффициентом корреляции нулевого порядка.

В выражении (4.2) частный коэффициент первого порядка (закреплен один фактор х₂ в скобках) выражается через коэффициенты нулевого порядка.

Частные коэффициенты корреляции второго порядка можно выразить через коэффициенты первого порядка при помощи соотношения

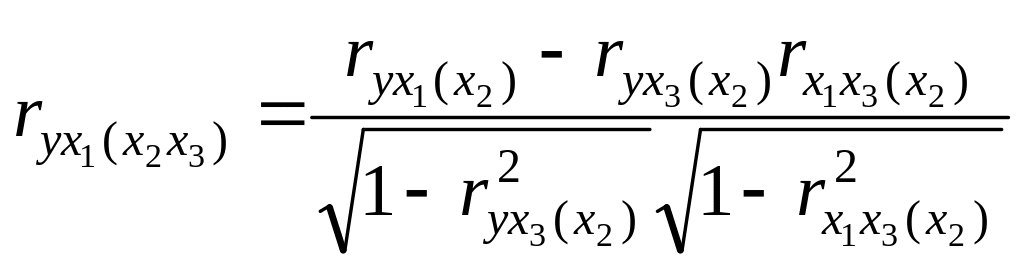(4.3)

Аналогично можно записать соотношения, выражающий частный коэффициент корреляции k-го порядка через коэффициенты (k-1)-го порядка. Частные коэффициенты корреляции изменяются по величине от 0 до 1.

Следует отметить, что малость частных коэффициентов корреляции низших порядков не гарантирует малости коэффициентов более высокого порядка. Например, и могут быть оба малыми, а может быть велик.

Предположим, , тогда (4.2) запишется в виде

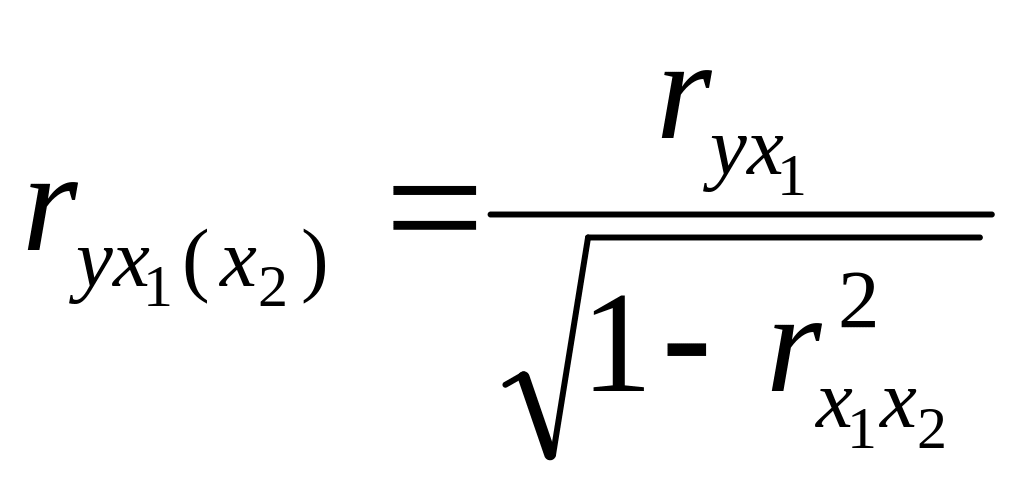(4.4)

если мал, а велик, то может быть также большим.

Пример 3.

Дано , , вычислить .

Решение.

После предварительного отбора факторов на основе парных и частных коэффициентов корреляции производятся оценки параметров , обычно они осуществляются по методу наименьших квадратов. Система нормальных уравнений в случае линейной зависимости (4.1) имеет вид

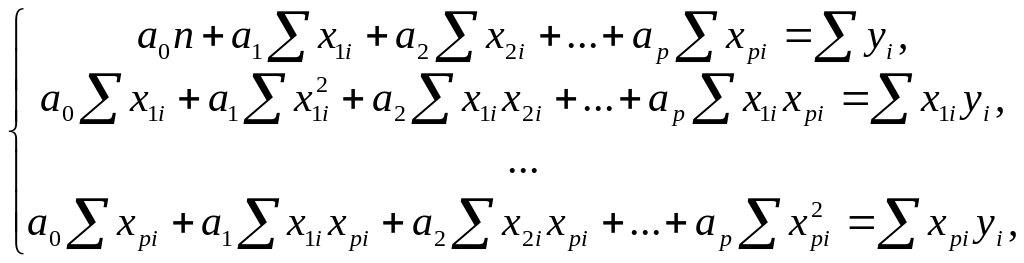
Решение такой системы может быть получено по теореме Крамера (с использованием определителей), методом Гаусса (последовательным исключением неизвестных) и другими методами.

3. Коэффициент множественной корреляции

Для определения тесноты связи между фактором у и совокупностью факторов в случае линейной зависимости применим коэффициент множественной корреляции R. Коэффициент изменяется в интервале от 0 до 1, причем, в отличие от коэффициентов парной корреляции, он берется по абсолютной величине. Если линейной корреляционной связи между у и нет то R=0. Если R=1, то связь функциональная. Выражение, по которому вычисляется коэффициент корреляции, имеет вид

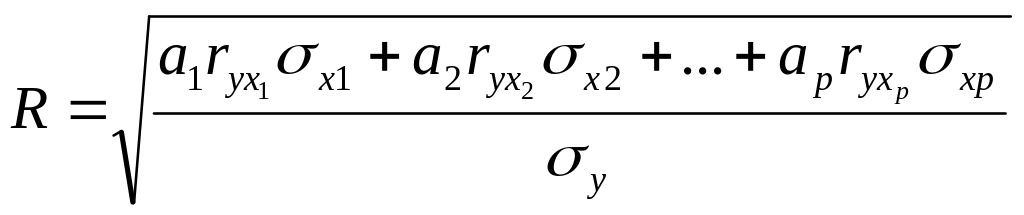
где – коэффициенты регрессии уравнения (4.1); – парные коэффициенты корреляции; – среднее квадратическое отклонение фактора ; – среднее квадратическое отклонение у.

Обычно интерпретируется не сам коэффициент корреляции R, а его квадрат R², который называется коэффициентом множественной детерминации. Напомним, что R² характеризует долю вариации зависимой переменной, обусловленной регрессией. Чем ближе R² к единице, тем лучше регрессия описывает зависимость между объясняющими переменными и зависимой переменной. Например, если коэффициент множественной корреляции R=0,7, то коэффициент множественной детерминации R²=0,49, т.е. 49% вариаций объясняется факторами, включенными в уравнение регрессии, а 51% – прочими факторами.

Существенность отличия от нуля выборочного коэффициента множественной корреляции проверяется на основе F-критерия (критерий Фишера). Вычисляется величина

(4.6)

где R – множественный коэффициент корреляции; p – число факторов ; n – число наблюдений.

Найденное значение критерия F сравнивается с F_табл при числе степеней свободы и заданном уровне значимости . Если расчетное значение F превышает табличное, то гипотеза о равенстве коэффициента множественной корреляции нулю отвергается и связь считается существенной.

Пример 4.

Дано: R=0,75, p=4, n=16, определить существенность связи.

Решение.

Вычислим критерий F по формуле (4.6):

F=0,5625∙(16-4-1)/4∙(1-0,5625)=3,53.

F_табл=3,36 при и уровне значимости 0,95. Расчетное значение F-критерия превышает табличное, поэтому можно сделать вывод о существенности связи.