Дискретные случайные величины.

8. Дискретная случайная величина Х задана законом распределения, представленным в таблице:

xi	-4	-3	-2	-1	1
pi	0,1	0,2c2	0,3	0,1c	0,3

1.Найти константу с. Ответ обосновать.

2.Найти математическое ожидание случайной величины Х.

3.Найти дисперсию случайной величины Х.

4.Построить график функции распределения случайной величины Х.

5.Найти вероятность Р{-3  X  1}.

Непрерывные случайные величины.

9. Плотность распределения непрерывной случайной величины Х имеет вид:

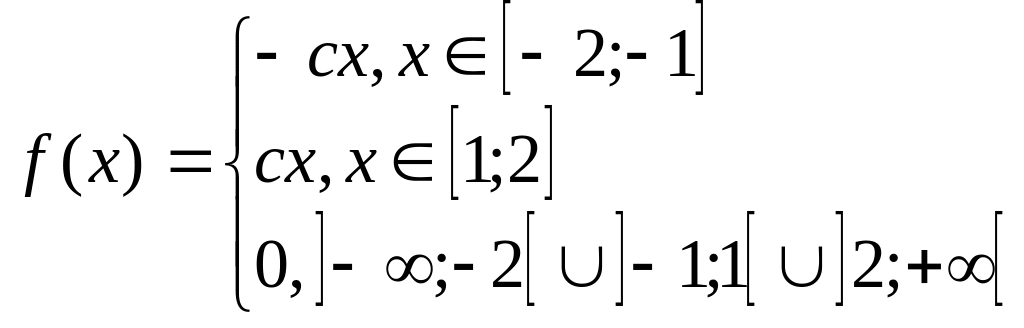
1.Найти константу с.

2.Найти математическое ожидание случайной величины Х.

3.Найти дисперсию случайной величины Х.

4.Построить графики плотности распределения и функции распределения случайной величины Х.

Найти P{X>0}, P{-1,5<X<1,5}.

Многомерные случайные величины.

10. Найти функцию распределения случайной величины Z=2X+Y, где X-дискретная случайная величина, принимающая два значения: 1 с вероятностью 0,3 и -1 c вероятностью 0,7, а Y имеет нормальное распределение с математическим ожиданием 0 и дисперсией 1; X и Y- независимы. Вычислить вероятность Р(Z<0).

Указание: воспользоваться формулой полной вероятности.

11. Непрерывная двумерная случайная величина (X,Y) равномерно распределена внутри прямоугольного треугольника с вершинами (-1;0), (4;0), (4;2). Найти двумерную плотность совместного распределения и плотности распределения случайных величин X и Y. Вычислить коэффициент корреляции.

Предельные теоремы теории вероятностей.

12. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит ровно 2 разбитых бутылки.

13. Отдел технического контроля проверяет 475 изделий на брак. Вероятность того, что изделие бракованное, равна 0,05. Найти вероятность того, что число бракованных изделий лежит в пределах от 15 до 33.

14. В осветительную сеть параллельно включено 20 ламп. Вероятность того, что за время Т лампа будет включена, равна 0,8. Пользуясь неравенством Чебышева, оценить вероятность того, что абсолютная величина разности между числом включенных ламп и средним числом (математическим ожиданием) включенных ламп за время Т окажется не меньше трех.

Математическая статистика.

15. По данному распределению выборки построить эмпирическую функцию распределения, гистограмму и полигон:

    xi	1	2	3	4	5	6
    ni	10	10	30	15	15	20

16. Найти точечную оценку параметра p биномиального распределения (схема Бернулли) по выборке (0,1,1,0,0,0,0,0,0,1,0,0), где Х принимает значения: 1 с вероятностью р и 0 с вероятностью 1-р: а) методом моментов и б) методом максимального правдоподобия.

17. Найти доверительный интервал надежности 1-α=0,99 для неизвестного математического ожидания при неизвестной дисперсии по выборке

№	1	2	3	4	5	6	7	8	9	10	11
X	9,9	12,5	10,3	9,2	6,0	10,9	10,3	11,8	11,6	9,8	14,0

Распределение нормальное. Какова точность этого интервала? Как изменится точность, если дисперсия известна и равна 4,2025?

18. Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза об экспоненциальном распределении генеральной совокупности с результатами наблюдений, представленными в таблице:

X	0,1	0,3	0,5	1	1,5	1,8	2,5	3,5	5	7
n	7	11	15	10	9	10	12	14	8	4