Методы прямоугольников

Идея метода прямоугольников заключается в том, что на малом отрезке [x₀;x₀+h] площадь криволинейной трапеции приближенно равна площади прямоугольника с основанием [x₀;x₀+h] и высотой, равной ординате в какой-то точке ξ  [x₀:x₀+h], т.е.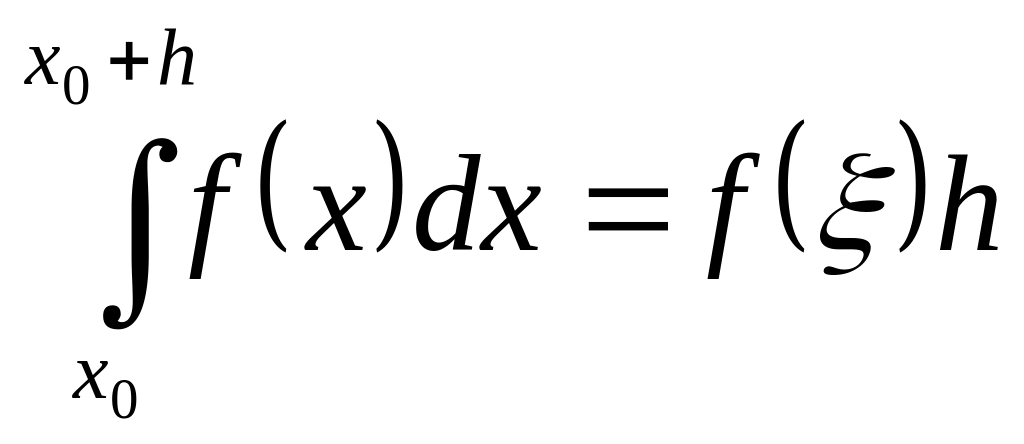 . В зависимости того, какую точку отрезка [x₀;x₀+h] выбирают в качестве ξ, и получают разновидности формулы прямоугольников.

Разобьем отрезок [a,b] на n равных частей точками

а=х₀, x_l=x₀+h, x₂=x_l+h, ….. , x_i=x_i-1+h, .…. , x_n=x_n-1+h=b, где .

На каждом частичном отрезке [x_i-1,x_i] заменим соответствующую криволинейную трапецию на прямоугольник, высоту которого можно определить по разному.

Р ис. 2.1.

1. ФОРМУЛА "ЛЕВЫХ" ПРЯМОУГОЛЬНИКОВ.

Если выбрать в качестве высоты прямоугольника на каждом из отрезков [x_i-1,x_i] (i=1,...,n) ординату в левом конце, т.е. Y_i-l=f(x_i-l), то криволинейная трапеция заменится на ступенчатую Фигуру, площадь S_n которой можно принять за площадь трапеции. Следовательно,

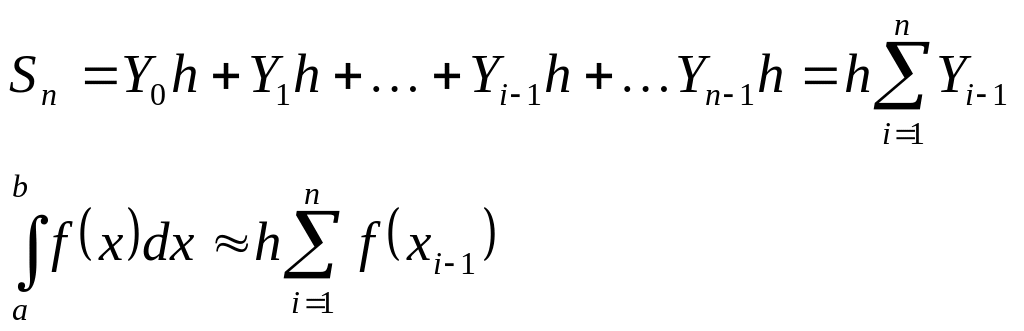(2.3)

2. ФОРМУЛА "ПРАВЫХ" ПРЯМОУГОЛЬНИКОВ.

Если в качестве высоты прямоугольника выбрать ординату, правого конца частичного отрезка, т.е. высота прямоугольника на отрезке [x_i-1,x_i]равна Y_i=f(x_i) (il=l,...,n), то для приближенного вычисления интеграла получим формулу "правых" прямоугольников;

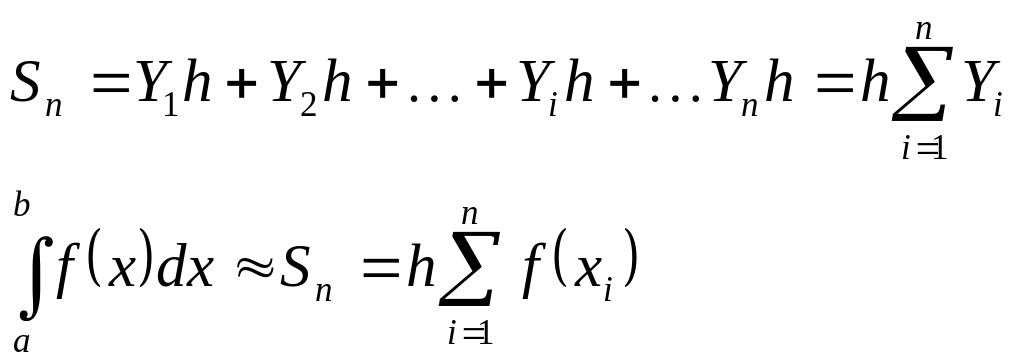(2.4)

3. ФОРМУЛА "СРЕДНИХ" ПРЯМОУГОЛЬНИКОВ.

Если в качестве высоты прямоугольника выбрать ординату, взятую в средней точке частичного отрезка, т.е. высота прямоугольника равна

то для приближенного вычисления интеграла получим формулу "средних" прямоугольников, т.е.

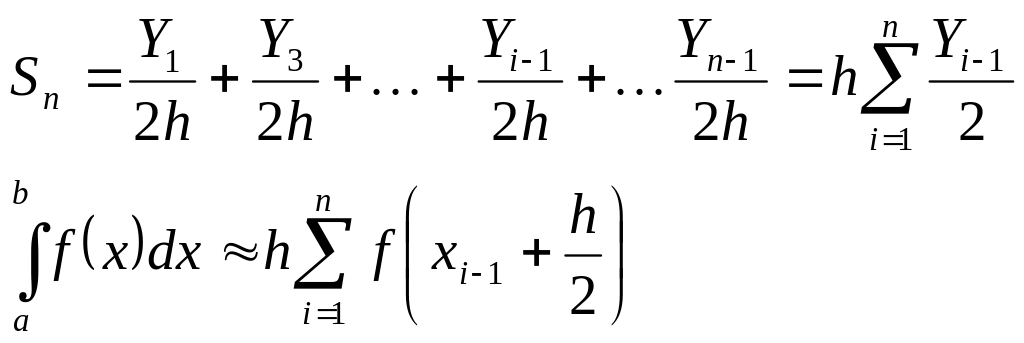(2.5)

Формулы (2.3)-(2.5) легко программируются при различных способах задания интегрируемой функции.

а) б) в)

Рис.2.2. Иллюстрация методов прямоугольников (а - метод "левых" прямоугольников; б - метод "правых" прямоугольников; в - метод "средних" прямоугольников).

ФОРМУЛА ТРАПЕЦИЙ.

На отрезке [x₀;x₀+h] дугу кривой Y=f(x) заменяют хордой, стягивающей концы этой дуги, т.е. производят линейное интерполирование функции Y=f(x). При этом площадь криволинейной трапеции заменяют площадью трапеции с основаниями f(x₀) и f(х₀+h) и высотой h, следовательно,

Отсюда, чтобы вычислить , разобьем отрезок [a,b] на n равных частичных отрезков, так что шаг .

Рис.2.3.

Проведем через точки деления ординаты и заменим данную кривую ломанной, отрезки которой соединяют концы двух соседних координат. Криволинейная трапеция при этом заменится на фигуру, состоящую из n трапеций, высоты которых равны h, а основания Y_i=f(x_i), (i=0, ... ,n) в точках деления. Площадь такой фигуры выражается формулой

,

а для вычисления интеграла имеем формулу

, (2.6)

которую называют формулой трапеций.