Течение в цилиндрической трубе

Рассмотрим напорное установившееся равномерное стабилизированное движение несжимаемой жидкости в горизонтальной прямой трубе круглого сечения. На определенном расстоянии от входа в трубу происходит формирование поля скорости -участок гидродинамической стабилизации длиной При дальнейшем продвижении потока вдоль трубы поле скорости остается неизменным, такое течение называется стабилизированным. Задача гидродинамики заключается в определении полей скорости, давления, потока импульса (тензора напряжений), а также коэффициентов импульсоотдачи или трения.

Решение данной задачи для течения в прямой трубе круглого сечения удобнее получить с использованием цилиндрических координат. Совместим ось x с осью трубы, а начало координат с концом участка гидродинамической стабилизации (рис. 14). Связь прямоугольной и цилиндрической системы координат осуществляется следующим образом:

(42)

где  - угол, между осями r и y.

Запишем уравнения движения и неразрывности в цилиндрических координатах для рассматриваемого случая. Для этого упростим общий вид данных уравнений с учетом следующих допущений. При стабилизированном осесимметричном течении составляющие скорости W_r и W_ = 0, следовательно, равны нулю и производные от них по любым переменным.

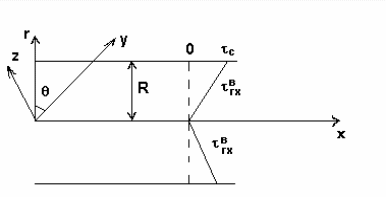
Рис. 14. Профиль потока импульса при установившемся стабилизированном течение в цилиндрической трубе.

Установившееся (стационарное) движение предполагает неизменность величин во времени, следовательно, . Предполагая, что длина горизонтальной трубы значительно превышает ее диаметр d, пренебрегаем изменением давления за счет гидростатического эффекта . Несжимаемость жидкости дает =сonst. С учетом вышесказанного уравнения движения и неразрывности приобретают вид

(43) (44)

Решив уравнение движения, можно получить зависимость потока импульса (элемента тензора вязких напряжений ) от гидравлического сопротивления трубопровода (как уже отмечалось для горизонтального равномерного движения потерянное давление р_n совпадает с перепадом давлений р). Проинтегрируем уравнение (43) по dr. Учитывая, что для равномерного движения , получим

или (45)

Поскольку пропорционален , а величина данной производной вследствие осесимметричности равна нулю при r = 0, то и . Из этого граничного условия находим, что постоянная интегрирования С = 0. Знак минус в решении (45) объясняется отрицательным значением производной (давление падает в направлении движения). Поток импульса направлен от оси трубы к стенкам, линейно возрастая от 0 до при r = R (рис. 14). Тогда для равномерного движения можно представить

(46) (47)

где - длина участка стабилизированного течения, на котором происходит падение давления р. Мы нашли зависимость потока импульса (r), связав её с потерей давления в трубопроводе. Для определения потери давления (гидравлического сопротивления), а также поля скорости W_x(r), коэффициентов импульсоотдачи  и трения С_f, _г необходимо учитывать режим течения среды, о котором можно судить по величине критерия Рейнольдса

(48)