
- •«Введение в теорию надёжности»
- •1 Основные определения и количественные показатели
- •1.1 Надёжность объектов как комплексное свойство
- •1.2 Классификация отказов и предельное состояние объекта
- •1.3 Единичные и комплексные показатели надёжности
- •Средняя наработка на отказ – это отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки
- •1.4.1 Состав и общие правила задания требований на надёжность
- •1.5 Аналитические зависимости между показателями надёжности
- •2 Расчёт показателей надёжности
- •2.1.1 Прикидочный расчёт надёжности
- •2.1.2 Ориентировочный расчёт надёжности
- •2.1.3 Окончательный (коэффициентный) расчёт надёжности
- •2.1.4 Методика оценки безотказности технических средств
- •2.2 Расчёт структурной надёжности резервированных систем
- •2.2.1 Классификация методов резервирования
- •2.2.2 Расчёт надёжности при общем и раздельном резервировании
- •2.2.7 Расчёт надёжности по схеме «гибели-размножения»
- •2.3 Расчёт надёжности программных средств
- •2.3.1 Основные определения теории надёжности программного обеспечения
- •2.3.2 Методика оценки числа оставшихся ошибок в программе
- •2.3.3 Методика расчёта интенсивности обнаружения ошибок в зависимости от времени эксплуатации программы
- •2.3.5 Рекомендации по повышению надёжности программного обеспечения
- •3 Расчёт показателей надёжности при проектировании
- •3.1 Расчёт функциональной надёжности системы
- •3.1.1 Определение термина «функциональная надёжность» системы
- •3.2 Анализ качества структурной схемы
- •3.2.1 Показатели качества структурной схемы
- •Распределение требований к надёжности элементов схемы
- •3.4 Сравнение различных методов повышения надёжности системы
- •3.4.1 Краткое описание основных методов повышения надёжности
- •3.4.2 Примеры, иллюстрирующие сложность проблемы повышения надёжности
Средняя наработка на отказ – это отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки
 (1.10)
(1.10)
где
 -
время исправной работы между
-
время исправной работы между
 и
и
 м
отказами объекта;
м
отказами объекта;
 - число отказов объекта.
- число отказов объекта.
При достаточно
большом числе отказов
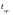 стремится
к среднему времени между двумя соседними
отказами. Если проводится испытание
нескольких однотипных объектов, то
среднее время между отказами определяют
из выражения
стремится
к среднему времени между двумя соседними
отказами. Если проводится испытание
нескольких однотипных объектов, то
среднее время между отказами определяют
из выражения
 число
объектов. (1.11)
число
объектов. (1.11)
Интенсивность отказов – это отношение числа отказавших объектов в единицу времени к среднему числу объектов, продолжающих исправно работать в данный интервал времени:
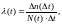 (1.12)
(1.12)
здесь
число
отказавших объектов за промежуток
времени от
 до
до
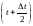 ,
а
,
а
 где
где
 число
исправно работающих объектов в начале
интервала времени
;
число
исправно работающих объектов в начале
интервала времени
;
 число
исправно работающих объектов в конце
интервала времени
число
исправно работающих объектов в конце
интервала времени

В теории надёжности принята модель интенсивности отказов объекта, характеризуемая приведённой ниже кривой интенсивности отказов объекта в процессе эксплуатации.
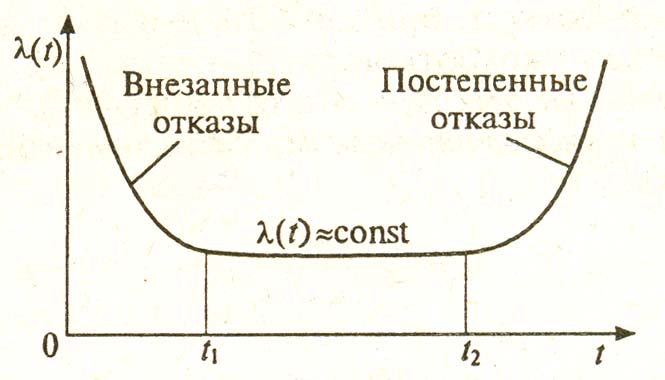
Рисунок 1.3 - Модель интенсивности отказов объекта
Параметр
потока отказов
– это отношение среднего числа отказов
восстанавливаемого объекта за произвольно
малую его наработку к значению этой
наработки. Этот показатель используют
для оценки безотказности восстанавливаемых
объектов в процессе эксплуатации: в
начальный период времени объект работает
до отказа; после отказа происходит
восстановление объекта, и объект вновь
работает до отказа и так далее. При этом
полагают, что восстановление объекта
происходит мгновенно. Для таких объектов
моменты отказов на оси суммарной
наработки (оси времени) образуют поток
отказов. В качестве характеристики
потока отказов используют - «ведущую
функцию»
 данного потока – математическое ожидание
числа отказов за время
t:
данного потока – математическое ожидание
числа отказов за время
t:
 (1.13)
(1.13)
Параметр потока
отказов
 характеризует среднее число отказов,
ожидаемых на малом интервале времени
характеризует среднее число отказов,
ожидаемых на малом интервале времени
 (1.14)
(1.14)

Статистически параметр потока отказов определяют по формуле
 (1.15)
(1.15)
где число отказов восстанавливаемого объекта за интервал времени от до .
Средний ресурс
 - это математическое ожидание ресурса.
- это математическое ожидание ресурса.
Гамма-процентный
ресурс
 %
- это наработка, в течение которой объект
не достигнет предельного состояния с
заданной вероятностью
,
выраженной в процентах. Формула для
расчёта аналогична формуле для
гамма-процентной наработке до отказа.
%
- это наработка, в течение которой объект
не достигнет предельного состояния с
заданной вероятностью
,
выраженной в процентах. Формула для
расчёта аналогична формуле для
гамма-процентной наработке до отказа.
Назначенный
ресурс
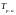 определяется как суммарная наработка
объекта, при достижении которой применение
по назначению должно быть прекращено.
определяется как суммарная наработка
объекта, при достижении которой применение
по назначению должно быть прекращено.
Средний срок
службы
 - математическое ожидание срока службы.
- математическое ожидание срока службы.
Гамма-процентный
срок службы
 %
- это календарная продолжительность от
начала эксплуатации объекта, в течении
которой он не достигнет предельного
состояния с заданной вероятностью
,
%.
%
- это календарная продолжительность от
начала эксплуатации объекта, в течении
которой он не достигнет предельного
состояния с заданной вероятностью
,
%.
Назначенный
срок службы
 - календарная продолжительность
эксплуатации объекта, при достижении
которой применение по назначению объекта
должно быть прекращено.
- календарная продолжительность
эксплуатации объекта, при достижении
которой применение по назначению объекта
должно быть прекращено.
Назначенный ресурс и назначенный срок службы устанавливают на основании субъективных или организационных предположений, и они являются косвенными показателями надёжности.
Момент
восстановления работоспособности
объекта после отказа является случайным
событием. Поэтому в качестве характеристики
ремонтопригодности используется функция
распределения этой случайной величины
 .
Вероятностью
восстановления называется
вероятность того, что время восстановления
работоспособного состояния объекта не
превысит заданного:
.
Вероятностью
восстановления называется
вероятность того, что время восстановления
работоспособного состояния объекта не
превысит заданного:

Вероятность
не восстановления
на заданном интервале
,
т.е. вероятность того, что
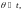 равна
равна

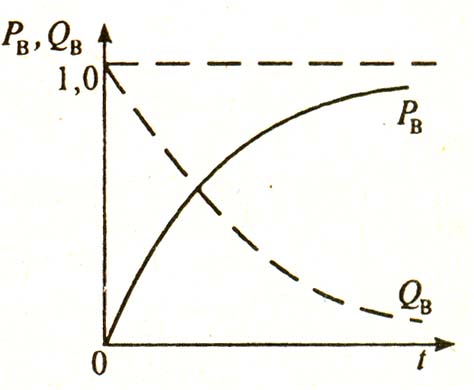
Рисунок 1.4 - Изменение вероятностей восстановления и не восстановления во времени
Плотность вероятности
момента восстановления равна

Средним временем восстановления является момент 1-го порядка (математическое ожидание) времени восстановления работоспособного состояния объекта.
 (1.16)
(1.16)
Статистически
среднее время восстановления равно
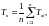 где
где
 -
время обнаружения и устранения
-
время обнаружения и устранения
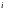 -
го отказа объекта.
-
го отказа объекта.
Важным показателем
ремонтопригодности объекта является
интенсивность
восстановления
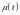 ,
которая, следуя общей методологии,
аналогична показателю безотказности
– интенсивности отказов
,
которая, следуя общей методологии,
аналогична показателю безотказности
– интенсивности отказов
 .
.
Показатели сохраняемости – средний срок сохраняемости и гамма-процентный срок сохраняемости – определяются аналогично соответствующим показателям безотказности и долговечности. Средний срок сохраняемости – это математическое ожидание срока сохраняемости; а гамма-процентный срок сохраняемости – это срок сохраняемости, достигаемый объектом с заданной вероятностью , %.
Так как вероятностные характеристики отдельных свойств надёжности полагают независимыми, то для оценки нескольких свойств надёжности используют комплексные показатели. Рассмотрим применяемые в теории надёжности комплексные показатели.
Коэффициент готовности – это вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается
 (1.17)
(1.17)
Коэффициент
оперативной готовности определяется
как вероятность того, что объект окажется
в работоспособном состоянии в произвольный
момент времени, кроме планируемых
периодов, в течение которых применение
объекта по назначению не предусматривается
и, начиная с этого момента, будет работать
безотказно в течение заданного интервала
времени
 :
:
 (1.18)
(1.18)
До этого момента такие объекты могут быть в режиме дежурства, но без выполнения заданных рабочих функций. В обоих режимах возможно возникновение отказов и восстановление работоспособности объекта.
Иногда пользуются коэффициентом простоя
 (1.19)
(1.19)
Коэффициент технического использования – это отношение математическое ожидание интервала времени наработки восстанавливаемого объекта к математическому ожиданию интервалов времени пребывания объекта в состояниях простоев, обусловленных техническим обслуживанием и ремонтами, за тот же период эксплуатации
 (1.20)
(1.20)
где
 математическое
ожидание наработки восстанавливаемого
объекта;
математическое
ожидание наработки восстанавливаемого
объекта;
 математическое
ожидание интервалов времени простоев
при техническом обслуживании;
математическое
ожидание интервалов времени простоев
при техническом обслуживании;
 математическое
ожидание времени, затрачиваемого на
плановые и внеплановые ремонты.
математическое
ожидание времени, затрачиваемого на
плановые и внеплановые ремонты.

 характеризует долю времени объекта в
работоспособном состоянии относительно
рассматриваемой продолжительности
эксплуатации.
характеризует долю времени объекта в
работоспособном состоянии относительно
рассматриваемой продолжительности
эксплуатации.
Коэффициент
планируемого применения
– это отношение разности заданной
продолжительности эксплуатации
 и математического ожидания суммарной
продолжительности плановых технических
обслуживаний
и математического ожидания суммарной
продолжительности плановых технических
обслуживаний
 и ремонтов
и ремонтов
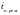 за тот же период эксплуатации к значению
этого периода
за тот же период эксплуатации к значению
этого периода
 (1.21)
(1.21)
Коэффициент сохранения эффективности – отношение значения показателя эффективности за определённую продолжительность эксплуатации Э к номинальному значению показателя Э0, вычисленному при условии, что отказы объекта в течение того же периода эксплуатации не возникают. Этот коэффициент характеризует степень влияния отказов элементов объекта на эффективность его применения по назначению
 (1.22)
(1.22)
При этом под эффективностью применения объекта понимают его свойство создавать определённый полезный результат (выходной эффект) в течение периода эксплуатации при определённых условиях. Показатель эффективности – показатель качества, характеризующий выполнение объектом его функций. Аналитические выражения для расчёта эффекта объектов различных типов приведены в ГОСТ 27.003-89. Выбор номенклатуры показателей надёжности и их нормирование осуществляют на основании ГОСТ 27.033-83.
1.4 Общий порядок обеспечения надёжности на стадиях
«жизненного» цикла объекта
В соответствии с ГОСТ 27.003-90 рассмотрим некоторые вопросы заданной темы.
