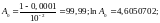2.3.3 Методика расчёта интенсивности обнаружения ошибок в зависимости от времени эксплуатации программы

В процессе комплексной отладки ПО видоизменяется с целью осуществления недостающих функций и внесения исправлений для обнаруженных ошибок в уже реализованной программе. Такие изменения обычно заносятся в специальный журнал учёта исправлений с указанием даты и семантики исправления. В качестве примера рассмотрим ПО из примера 1. Исходными данными являются результаты комплексной отладки этого ПО примерно за двухлетний период. Количество обнаруженных ошибок фиксировалось помесячно, поэтому интенсивность обнаружения ошибок имеет размер «количество ошибок/месяц». Значения интенсивности обнаружения ошибок за 20 месяцев приведены ниже в таблице. Таблица 2.3 - Значения интенсивности обнаружения ошибок

Δti	1	2	3	4	5	6	7	8	9	10
r(ti)	10	14	7	4	5	9	3	8	13	9
Δti	11	12	13	14	15	16	17	18	19	20
r(ti)	5	7	9	2	5	6	4	2	1	2

Используя экспоненциальную аппроксимацию что даёт значение количества оставшихся ошибок Это значение хорошо согласуется с ранее определенными значениями и .

Экспоненциальная аппроксимация интенсивности обнаружения ошибок может быть использована для прогностического расчёта количества оставшихся ошибок, если определить интенсивность определения ошибок на какое-то время вперед, например, на квартал.

Таблица 2.4 - Интенсивность обнаружения ошибок на квартал вперед

Δti	21	22	23
r(ti)	2	2	2

2.3.4 Статистическая оценка вероятности безотказной работы

программного обеспечения

Рассмотрим метод последовательного анализа для оценки вероятности безотказной работы программы. В нём вводится допущение о том, что если вероятность успешного прогона Р находится в достаточно малой окрестности точки Р₀, то риск принятия неправильного решения допустимо мал. Под неправильным решением понимают решение отвергнуть надёжную программу или пропустить не надёжную программу. Для формализации этого допущения задают такие P` и P`` (P`<P₀<P``), что принятие не надёжной программы рассматривается как ошибочное решение только при , а отказ от надёжной программы является ошибочным в случае, когда . После задания значений вероятностей P` и P`` допустимый риск принятия неправильных решений таков, что вероятность ошибки первого рода, т.е. отказа от надёжной программы, не должна превышать α = Вер , а вероятность ошибки второго рода, т.е. принятия не надёжной программы не должна превышать β = Вер . Значения величин α и β при этом назначаются, исходя из разумного компромисса, до начала испытаний, так как с их уменьшением растёт объём испытаний.

Сущность последовательного анализа гипотезы Н₀ (Р = Р₀) состоит в проверке двух конкурирующих гипотез Н`(P = P`) и H``(P = P``). Здесь под вероятностью безотказной работы ПО P(m) понимают вероятность получения выборки в которой для элементов P`<P_m,P``, тогда

(2.111)

Если верна гипотеза H`, то

(2.112)

Аналогично, если верна гипотеза H``, то

(2.113)

Составим отношение «правдоподобия»:

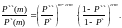(2.114)

Последовательный анализ проводится до тех пор, пока не будет выполняться следующие неравенства:

(2.115)

Если на этапе m 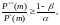то ПО не надёжно; а если то ПО можно принять как надёжное.

Прологарифмировав выражения (2.114) и (2.115), можно придать им графическую форму в координатах m , . После логарифмирования и преобразований получим :

Теперь можно построить две прямые и Если то ПО не надёжно, если же то ПО можно принять как надёжное. При условии испытания следует продолжать.

На плоскости строятся прямые с одинаковым наклоном и точками пересечения оси ординат и соответственно.

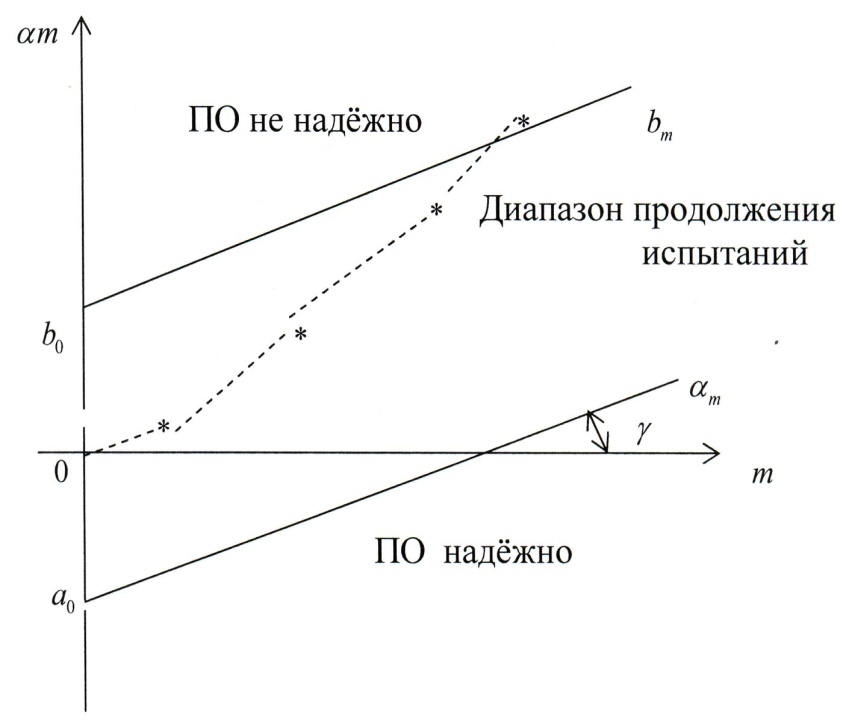
Рисунок 2.12 - Примерные графические результаты

последовательного анализа

Итак, план действий при выполнении последовательного анализа является таковым:

• задать перед началом испытаний значения величин

• построить прямые линии и 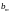, как это сделано на рис. 2.12;

• в ходе испытаний наносить на график полученные точки ( );

• если текущая точка попадает выше линии , то испытания завершаются, а ПО признаётся не удовлетворяющим заданным требованиям по надёжности;

• если текущая точка попадает ниже линии , то испытания завершаются, а ПО признаётся надёжным ;

• испытания продолжаются, если текущая точка находится внутри области ограниченной прямыми и .

Изложенный метод удобен и прост в практической работе. Следует отметить, что метод последовательного анализа требует обеспечения независимости испытаний (прогонов) программы. Для обеспечения независимости прогонов могут быть использованы различные генераторы тестовых наборов данных. В них генерация числовых значений, выбор символических значений и значений ключевых полей осуществляется с помощью алгоритмов, выдающих совокупности случайных чисел с последующим формированием потоков входных сообщений, модельных экземпляров баз данных разнообразной структуры. Для автоматизации последовательного анализа разработаны специальные программы.

При использовании метода последовательного анализа очень важно оценить среднее число испытаний при истинности гипотезы H` и среднее число испытаний при истинности гипотезы H``. В первом случае

(2.116)

где 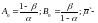математическое ожидание случайной величины при истинности гипотезы H`. Очевидно, что

Во втором случае

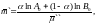(2.117)

где математическое ожидание случайной величины при истинности гипотезы H``,

Рассмотрим примеры расчёта среднего числа испытаний.

Пример 3. Пусть Необходимо определить среднее число испытаний программы.

Решение.

Пример 4. Пусть Определить среднее число испытаний программного обеспечения.

Решение.